Os teoremas de probabilidade são a base para entender e resolver problemas envolvendo eventos em espaços amostrais finitos. Eles ajudam a calcular probabilidades, analisar relações entre eventos e simplificar situações complexas. Neste artigo, exploraremos os principais teoremas de probabilidade, explicando cada um com detalhes e fornecendo exemplos práticos e inéditos para facilitar o aprendizado.

Teorema do Evento Certo
A Probabilidade do Evento Certo é 1 ou 100%
O evento certo é aquele que sempre ocorre porque inclui todos os resultados do espaço amostral (S). Sua probabilidade é definida como P(S) = 1.
Exemplo 1: Lançamento de um dado
Ao lançar um dado de seis faces, qual é a probabilidade de obter um número entre 1 e 6?
Solução:
Espaço amostral: S = {1, 2, 3, 4, 5, 6}
Evento certo: “Obter qualquer número entre 1 e 6”. P(S) = 1
Exemplo 2: Sorteio de uma bola
Uma urna contém 10 bolas numeradas de 1 a 10. Qual é a probabilidade de retirar uma bola que pertença ao conjunto S = {1, 2, 3, …, 10\}?
Solução:
Evento certo: “Retirar qualquer bola da urna”. P(S) = 1
A probabilidade é 1 porque todos os números de 1 a 10 pertencem ao espaço amostral.
Teorema da Inclusão de Eventos
Se A⊂B, então P(A) ≤ P(B)
Se A é um subconjunto de B, todos os resultados favoráveis a A também são favoráveis a B. Logo, a probabilidade de A será menor ou igual à de B.
Exemplo 1: Lançamento de dois dados
Considere o espaço amostral dos possíveis resultados ao lançar dois dados:
S={(1, 1), (1, 2), …, (6, 6)}
- Evento A: “A soma dos números é 3”. A = {(1,2), (2,1)}.
- Evento B: “A soma dos números é menor ou igual a 4”.
B = {(1,1), (1,2), (2,1), (3,1), (2,2)}.
Como A ⊂ B, temos P(A) ≤ P(B)
Cálculo das probabilidades:
P(A) = 2/36,
P(B) = 5/36
P(A) = 2/36 ≤ 5/36 = P(B)
Exemplo 2: Sorteio de cartas
Considere um baralho com 52 cartas:
- Evento A: “Tirar uma carta de copas menor que 8”. A = {2, 3, 4, 5, 6, 7} (6 cartas).
- Evento B: “Tirar uma carta de copas”. B={Ás, 2, …, Rei} (13 cartas).
Como A ⊂ B, P(A) ≤ P(B):
P(A) = 6/52 ≤ 13/52 = P(B)
Teorema da Limitação da Probabilidade
0 ≤ P(A) ≤ 1
A probabilidade de qualquer evento A está sempre entre 0 e 1. Isso ocorre porque A é um subconjunto do espaço amostral S, e sua probabilidade nunca será negativa nem maior que 1.
Exemplo 1: Sorteio de números
Ao sortear um número de 1 a 100, qual é a probabilidade de um número ser maior que 150?
Solução:
Evento impossível: A=∅. P(A) = 0
A probabilidade é P(A) = 0 porque não há números maiores que 150 no intervalo de 1 a 100.
Exemplo 2: Lançamento de uma moeda
Ao lançar uma moeda, o espaço amostral é S={cara, coroa}:
- Evento A: “Obter cara”.
- Probabilidade:
P(A) = 1/2 = 0,5
Aqui, 0 ≤ P(A) ≤ 1, como esperado.
Teorema da União de Eventos
P(A∪B) = P(A) + P(B) − P(A∩B)
A probabilidade da união de dois eventos A e B é a soma das probabilidades de A e B, subtraindo a probabilidade da interseção para evitar a contagem duplicada.

Exemplo 1: Lançamento de dois dados
Considere o espaço amostral: S={(1, 1), …,(6, 6)}:
- Evento A: “A soma dos números é 7”. A = {(1, 6), (2, 5), (3, 4), (4, 3), (5, 2), (6, 1)}
- Evento B: “O primeiro dado é 5”. B = {(5, 1), (5, 2), …, (5, 6)}.
Interseção A∩B: “A soma é 7 e o primeiro dado é 5”. A∩B = {(5,2)}
Cálculo:

Exemplo 2: Seleção de alunos
Uma sala tem 20 alunos, sendo 12 meninos e 8 meninas.
- Evento A: “Selecionar um menino”. P(A)=12/20
- Evento B: “Selecionar alguém que use óculos” (5 meninos e 3 meninas).
P(B) = 8/20
- Interseção: “Selecionar um menino que usa óculos”.
- P(A∩B) = 5/20
Cálculo:
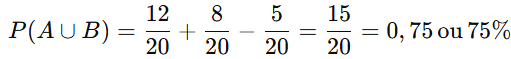
Caso Particular: Eventos Mutuamente Exclusivos
Se A∩B = ∅ (eventos mutuamente exclusivos), então: P(A∪B) = P(A) + P(B)
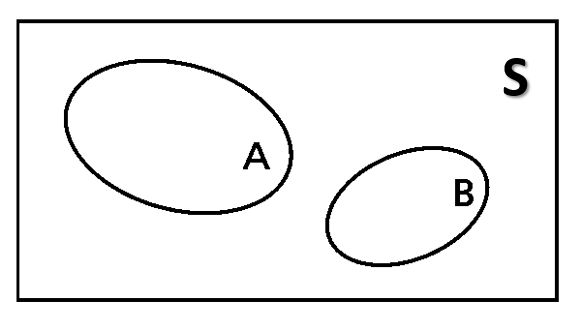
Teorema do Conjunto Complemento
P(AC) = 1 − P(A)
O complemento de um evento A, denotado AC, ocorre quando A não ocorre. A soma das probabilidades de A e AC é sempre igual a 1.

Exemplo 1: Sorteio de bolas
Uma urna contém 5 bolas azuis e 7 bolas vermelhas (12 no total).
Evento A: “Retirar uma bola azul”. P(A) = 5/12
Complemento AC: “Não retirar uma bola azul”.

Exemplo 2: Prova com questões
Em uma prova de 10 questões, um aluno responde 7 corretamente.
Evento A: “Responder corretamente”. P(A)=7/10
Complemento AC:
“Responder incorretamente”.

Conclusão
Os teoremas de probabilidade em espaço amostral finito fornecem as ferramentas essenciais para analisar eventos e calcular probabilidades. Com exemplos variados e aplicações práticas, eles se tornam um recurso indispensável para estudantes, professores e profissionais que trabalham com análise de dados e tomadas de decisão.













