Na Geometria Euclidiana, você aprendeu que a soma dos ângulos internos de um triângulo qualquer é \(180^\circ\). Quando o triângulo é retângulo (isto é, possui um ângulo reto), os outros dois ângulos são agudos e complementares.
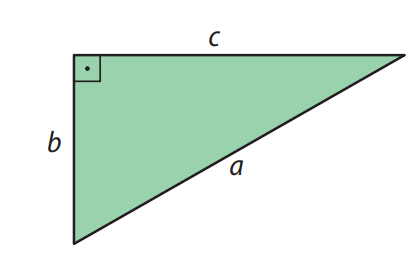
O lado oposto ao ângulo reto é chamado de hipotenusa, e os lados adjacentes ao ângulo reto são chamados de catetos.
Figura 1: Representação dos catetos e da hipotenusa
📐 Teorema de Pitágoras
O Teorema de Pitágoras afirma que, em um triângulo retângulo, o quadrado da medida da hipotenusa é igual à soma dos quadrados dos catetos:
- \(a\): medida da hipotenusa
- \(b\) e \(c\): medidas dos catetos
📏 Outras Relações Métricas no Triângulo Retângulo
Além do Teorema de Pitágoras, há outras relações entre os lados, projeções e altura do triângulo retângulo.
Figura 3: Elementos do triângulo retângulo
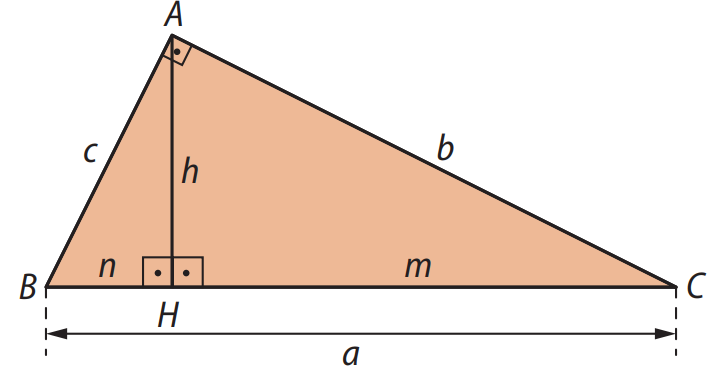
1. Quadrado dos catetos
2. Altura relativa à hipotenusa
3. Produto dos catetos
4. Proporções por semelhança
$$\frac{\textcolor{#0000cc}{a}}{\textcolor{#009900}{c}} = \frac{\textcolor{#009900}{c}}{\textcolor{#ff6600}{n}} \Rightarrow \textcolor{#009900}{c^2} = \textcolor{#0000cc}{a} \cdot \textcolor{#ff6600}{n}$$
$$\frac{\textcolor{#9933cc}{h}}{\textcolor{#ff6600}{n}} = \frac{\textcolor{#009900}{c}}{\textcolor{#9933cc}{h}} \Rightarrow \textcolor{#9933cc}{h^2} = \textcolor{#ff6600}{m} \cdot \textcolor{#ff6600}{n}$$
$$\frac{\textcolor{#0000cc}{a}}{\textcolor{#9933cc}{h}} = \frac{\textcolor{#9933cc}{h}}{\textcolor{#0000cc}{a}} \Rightarrow \textcolor{#0000cc}{a} \cdot \textcolor{#9933cc}{h} = \textcolor{#cc0000}{b} \cdot \textcolor{#009900}{c}$$
📌 Conclusão
Essas relações permitem resolver muitos problemas com triângulos retângulos, desde aplicações geométricas até questões em provas e concursos.
$$\textcolor{#0000cc}{a^2} = \textcolor{#cc0000}{b^2} + \textcolor{#009900}{c^2}$$
$$\textcolor{#cc0000}{b^2} = \textcolor{#0000cc}{a} \cdot \textcolor{#ff6600}{m} \quad , \quad \textcolor{#009900}{c^2} = \textcolor{#0000cc}{a} \cdot \textcolor{#ff6600}{n}$$
$$\textcolor{#9933cc}{h^2} = \textcolor{#ff6600}{m} \cdot \textcolor{#ff6600}{n}$$
$$\textcolor{#0000cc}{a} \cdot \textcolor{#9933cc}{h} = \textcolor{#cc0000}{b} \cdot \textcolor{#009900}{c}$$
🧠 Continue Estudando com Exercícios!
👉 Veja 10 questões resolvidas com passo a passo sobre semelhança de triângulos!
📥 E baixe gratuitamente nossos 10 eBooks com mapas mentais de Matemática para estudar com mais organização!
🔢 Questão 7 — Diagonal do Quadrado
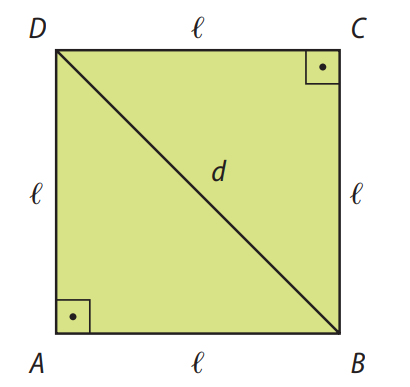
Enunciado: Considere o quadrado, cujo lado mede \( \ell \) e cuja diagonal mede \( d \). Calcule o valor de \( d \) em função de \( \ell \).
Figura:
🔢 Questão 8 — Raio de circunferência com corda e altura
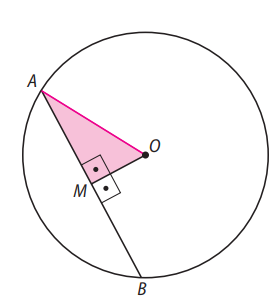
Enunciado: Uma circunferência tem raio desconhecido. Sobre ela, marcam-se uma corda \( \overline{AB} \) de 8 cm de comprimento e um segmento \( \overline{OM} \) perpendicular a \( \overline{AB} \), de 2 cm de comprimento, de modo que \( M \) é ponto de \( \overline{AB} \) e \( O \) é o centro da circunferência. Com esses dados, determine a medida do raio da circunferência.
Figura:
