📘 Tipos de Funções – Teoria e Exemplos Resolvidos
Introdução
O estudo das funções é essencial no Cálculo e em muitas áreas da matemática. Neste artigo, vamos revisar os principais tipos de funções: função potência, racional, exponencial, logarítmica e trigonométrica, destacando suas propriedades, gráficos e aplicações, com exemplos resolvidos para fixação.
🔶 1. Função Potência
📌 Definição
Uma função potência é definida como:
f(x) = a ⋅ xⁿonde:
– a é uma constante real
– n é um número real (inteiro ou fracionário)
📊 Gráficos e comportamento
- Se n é par, o gráfico é simétrico em relação ao eixo y.
- Se n é ímpar, o gráfico é simétrico em relação à origem.
- Se n < 0, a função é decrescente nos intervalos positivos e negativos (exceto para x = 0).
✅ Exemplo Resolvido
Exemplo 1: Esboce o gráfico de f(x) = x³
- A função é crescente em todo o domínio.
- Passa pelo ponto (0,0).
- É simétrica em relação à origem.
🔷 2. Função Racional
📌 Definição
Uma função racional é uma razão entre dois polinômios:
f(x) = p(x) / q(x), q(x) ≠ 0📊 Propriedades
- Domínio: todos os valores reais, exceto os que anulam
q(x). - Assíntotas verticais: valores de x que anulam o denominador.
- Assíntotas horizontais/oblíquas: analisadas pelo grau dos polinômios.
✅ Exemplo Resolvido
Exemplo 2: f(x) = (x² - 1) / (x - 1)
f(x) = [(x - 1)(x + 1)] / (x - 1) = x + 1, com x ≠ 1A função é igual a x + 1, com um buraco no ponto x = 1.
🔺 3. Função Exponencial
📌 Definição
A função exponencial tem a forma:
f(x) = a^xonde a > 0 e a ≠ 1.
📊 Propriedades
- O gráfico nunca toca o eixo x.
- Passa pelo ponto (0,1).
- Crescente se
a > 1, decrescente se0 < a < 1.

✅ Exemplo Resolvido
Exemplo 3: Calcule f(x) = 2^x para x = -2, 0, 2
f(-2) = 1/4f(0) = 1f(2) = 4
🔻 4. Função Logarítmica
📌 Definição
A função logarítmica é definida como:
f(x) = logₐ(x), com a > 0 e a ≠ 1📊 Propriedades
- Domínio:
x > 0 - Passa pelo ponto
(1, 0) - Crescente se
a > 1, decrescente se0 < a < 1

✅ Exemplo Resolvido
Exemplo 4:
log₂(8) = 3log₁₀(0,01) = -2
🟢 5. Funções Trigonométricas
As funções seno, cosseno e tangente são fundamentais no estudo de ângulos, ciclos e fenômenos periódicos.
📘 Função Seno
f(x) = sen(x)- Domínio: todos os reais
- Imagem: [–1, 1]
- Período: 2π

Exemplo:
sen(0) = 0sen(π/2) = 1sen(π) = 0
📗 Função Cosseno
f(x) = cos(x)- Mesmo domínio e imagem da função seno
cos(0) = 1,cos(π) = -1

📙 Função Tangente
f(x) = tan(x) = sen(x)/cos(x)- Domínio:
x ≠ π/2 + kπ - Imagem: todos os reais
- Período: π

🧠 Conclusão
Entender os diferentes tipos de funções é fundamental para dominar o Cálculo e resolver problemas matemáticos complexos. Este artigo apresentou uma síntese clara de cada tipo de função, com exemplos práticos e explicações visuais. Para consolidar, o ideal é praticar com muitos exercícios gráficos e algébricos.
✅ Exercícios Resolvidos – Tipos de Funções
🔶 1. Função Potência
Exercício 1: Esboce o gráfico de f(x) = x³
- Função ímpar, simétrica à origem
- Crescente em todo
ℝ - Pontos: (−2,−8), (−1,−1), (0,0), (1,1), (2,8)

Exercício 2: Determine f(x) = x−2
- a) f(1) = 1
- b) f(2) = 1/4
- c) f(−1) = 1
O gráfico possui assíntotas nos eixos, e imagem positiva.
Exercício 3: Esboce o gráfico de f(x) = x1/3
- Pontos: (−8,−2), (−1,−1), (0,0), (1,1), (8,2)
- Função definida em
ℝ, simétrica à origem

🔷 2. Função Racional
Exercício 1: f(x) = (x² − 1)/(x − 1)
Solução: f(x) = x + 1, com buraco em x = 1.
Exercício 2: Determine assíntotas de f(x) = (x² + 1)/(x² − 4x + 3)
Solução: Assíntotas verticais em x = 1 e x = 3 (raízes do denominador).
Exercício 3: Simplifique f(x) = (x² − 9)/(x + 3)
Solução: f(x) = x − 3, com buraco em x = −3.

🔺 3. Função Exponencial
Exercício 1: f(x) = 2^x
- f(−2) = 0,25
- f(0) = 1
- f(2) = 4
Exercício 2:
- a)
4^x = 64 ⇒ x = 3 - b)
(1/3)^x = 27^−1 ⇒ x = 3
Exercício 3: Esboce os gráficos de:
- a)
f(x) = 3^x– Crescente - b)
f(x) = (1/4)^x– Decrescente


🔻 4. Função Logarítmica
Exercício 1:
log₂(8) = 3log₁₀(0,01) = −2
Exercício 2:
- a)
log₃(x) = 2 ⇒ x = 9 - b)
log₅(x − 1) = 1 ⇒ x = 6
Exercício 3: Esboce o gráfico de f(x) = log₂(x)
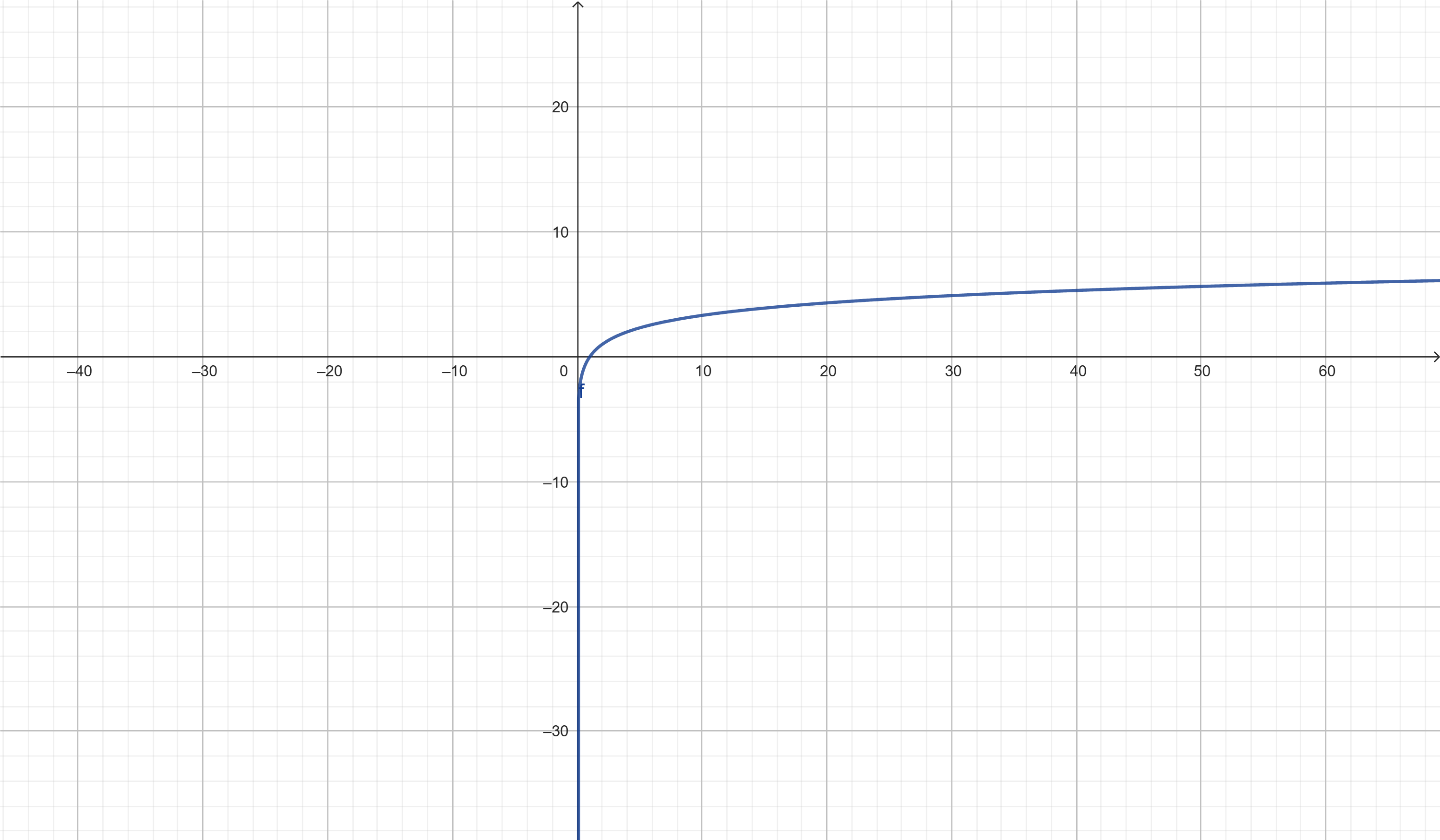
Exercício 4: Esboce o gráfico de f(x) = log(1/2)(x)
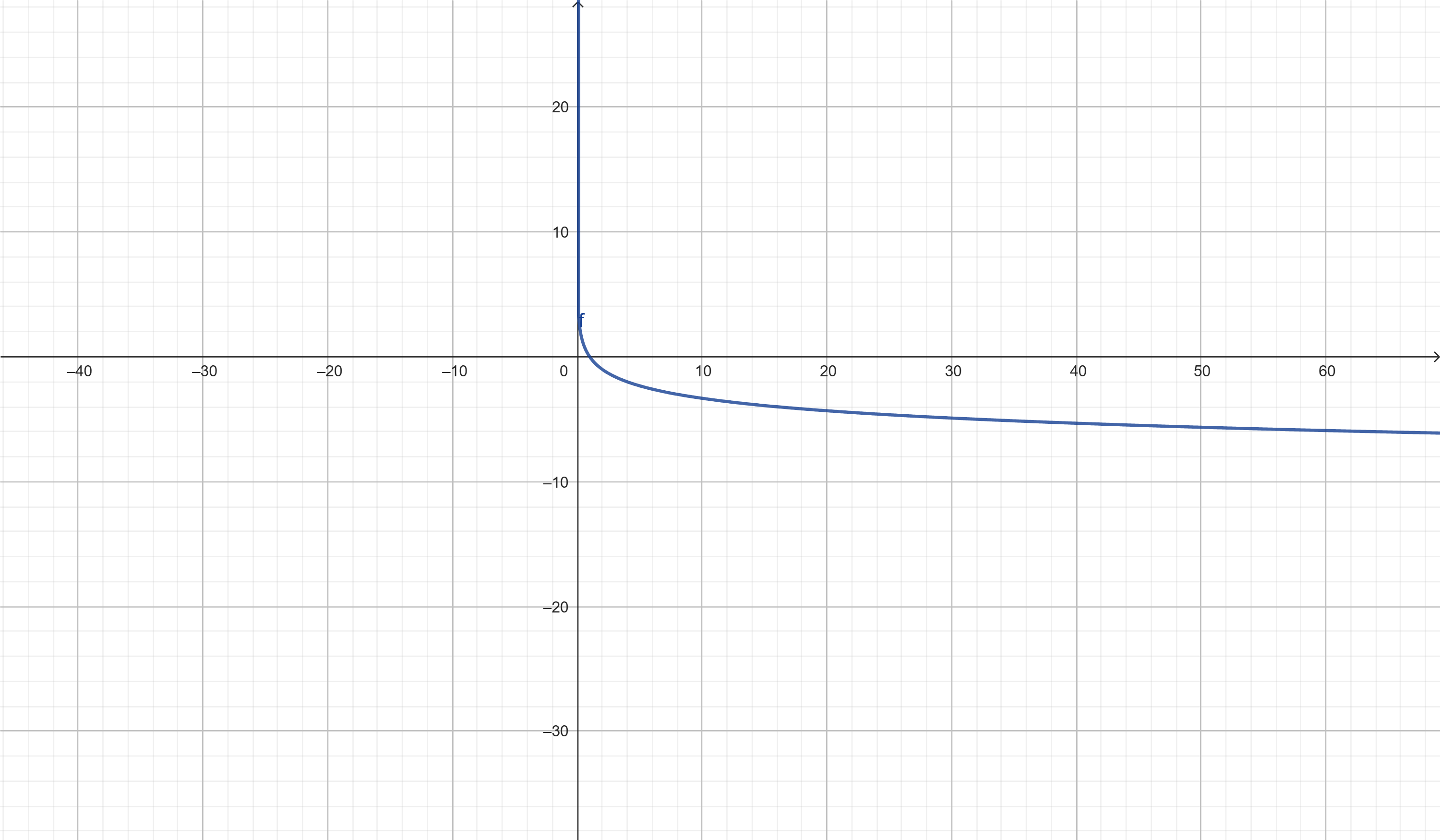
Solução: A segunda é deslocada 3 unidades para a direita. Domínio: x > 3.
🟢 5. Funções Trigonométricas
Exercício 1: Seno nos principais ângulos
sen(0) = 0sen(π/2) = 1sen(π) = 0
Exercício 2: Complete:
| Ângulo | Seno | Cosseno | Tangente |
|---|---|---|---|
| 120° | √3/2 | −1/2 | −√3 |
| 135° | √2/2 | −√2/2 | −1 |
| 150° | 1/2 | −√3/2 | −1/√3 |
Exercício 3:
- a)
sen(x) = −√3/2 ⇒ x = 4π/3 e 5π/3 - b)
tan(x) = 0 ⇒ x = 0, π, 2π
Exercício 4: Esboce o fráfico de f(x) = sen(x)

Exercício 5: Esboce o fráfico de f(x) = cos(x)

Exercício 6: Esboce o fráfico de f(x) = tg(x)























