A Matemática Financeira é essencial para entender operações que envolvem o valor do dinheiro ao longo do tempo. Neste artigo, abordaremos os conceitos de aumento, desconto, juros simples e juros compostos, utilizando notações e fórmulas específicas, e exemplos resolvidos para cada um.
1. Aumento
O aumento é a operação financeira que eleva o valor inicial (Vi) de um produto ou serviço em uma certa porcentagem. O aumento é aplicado diretamente sobre o valor inicial, resultando em um valor final (Vf).
Fórmula:
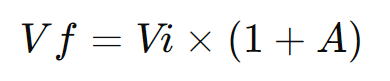
onde:
- ( Vi ) é o valor inicial,
- ( A ) é a porcentagem de aumento,
- ( Vf ) é o valor final após o aumento.
Exemplo Resolvido:
Um produto custa inicialmente R$ 200,00. Se for aplicado um aumento de 15%, qual será o valor final do produto?
Vf = 200.(1 + 0,15) = 200 . 1,15 = R$ 230,00
O valor final do produto após o aumento será de R$ 230,00.
2. Desconto
O desconto é a operação que reduz o valor inicial (Vi) de um produto ou serviço em uma certa porcentagem. O desconto é aplicado diretamente sobre o valor inicial, resultando em um valor final (Vf).
Fórmula:
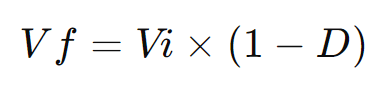
onde:
- ( Vi ) é o valor inicial,
- ( D ) é a porcentagem de desconto,
- ( Vf ) é o valor final após o desconto.
Exemplo Resolvido:
Um produto custa inicialmente R$ 300,00. Se for aplicado um desconto de 20%, qual será o valor final do produto?
Vf = 300 . (1 – 0,20) = 300 . 0,80 = R$ 240,00
O valor final do produto após o desconto será de R$ 240,00.
3. Juros Simples
O juros simples é calculado sobre o valor inicial (capital) durante todo o período de aplicação. Esse tipo de juros não considera o acúmulo de juros sobre juros.
Fórmula:
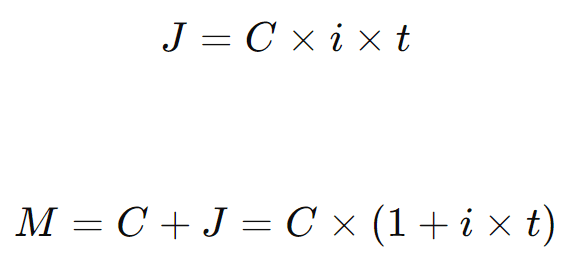
onde:
- ( J ) é o valor dos juros,
- ( M ) é o montante ou valor final,
- ( C ) é o capital ou valor inicial,
- ( i ) é a taxa de juros,
- ( t ) é o tempo.
Exemplo Resolvido:
Um capital de R$ 1.000,00 é aplicado a uma taxa de juros simples de 5% ao mês durante 6 meses. Qual será o montante ao final desse período?
J = 1000 . 0,05 . 6 = R$ 300,00
M = 1000 + 300 = R$ 1300,00
O montante ao final do período será de R$ 1.300,00.
4. Juros Compostos
O juros compostos é calculado sobre o montante acumulado a cada período, ou seja, os juros de cada período são incorporados ao capital para o cálculo dos juros do período seguinte.
Fórmula:
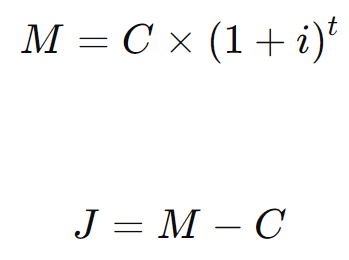
onde:
- ( M ) é o montante ou valor final,
- ( C ) é o capital ou valor inicial,
- ( i ) é a taxa de juros,
- ( t ) é o tempo,
- ( J ) é o valor dos juros acumulados.
Exemplo Resolvido:
Um capital de R$ 1.000,00 é aplicado a uma taxa de juros compostos de 3% ao mês durante 4 meses. Qual será o montante ao final desse período?
M = 1000 .(1 + 0,03)4
M = 1000 . (1,03)4 = 1000 . 1,1255 = R$ 1125,51
J = 1125,51 – 1000 = R$ 125,51
O montante ao final do período será de R$ 1.125,51, e o juros acumulado será de R$ 125,51
Considerações Finais
A Matemática Financeira é uma disciplina fundamental para a compreensão das operações econômicas que impactam nossas vidas cotidianas. Conhecer os conceitos de aumento, desconto, juros simples e juros compostos permite uma análise mais consciente e precisa de investimentos, compras e financiamentos.
Lista de Exercícios: Matemática Financeira
1. Aumento
Um produto custa R$ 500,00 e sofre um aumento de 10%. Qual será o valor final do produto?
- a) R$ 510,00
- b) R$ 550,00
- c) R$ 525,00
- d) R$ 575,00
2. Desconto
Um celular que custa R$ 1.200,00 está em promoção com um desconto de 15%. Qual será o valor final do celular?
- a) R$ 1.020,00
- b) R$ 1.100,00
- c) R$ 1.050,00
- d) R$ 1.080,00
3. Juros Simples
Um capital de R$ 2.000,00 é aplicado a uma taxa de 4% ao mês por 8 meses. Qual será o montante ao final do período?
- a) R$ 2.640,00
- b) R$ 2.800,00
- c) R$ 2.720,00
- d) R$ 2.560,00
4. Juros Compostos
Uma quantia de R$ 3.000,00 é investida a uma taxa de 2% ao mês por 6 meses. Qual será o montante ao final do período?
- a) R$ 3.372,00
- b) R$ 3.360,00
- c) R$ 3.400,00
- d) R$ 3.380,00
5. Aumento
Uma empresa decide aumentar o preço de um serviço que custa R$ 750,00 em 8%. Qual será o novo preço do serviço?
- a) R$ 810,00
- b) R$ 765,00
- c) R$ 780,00
- d) R$ 810,50
6. Desconto
Uma televisão custa R$ 2.500,00, mas com um desconto de 20%, qual será o valor pago?
- a) R$ 2.000,00
- b) R$ 2.100,00
- c) R$ 2.050,00
- d) R$ 2.200,00
7. Juros Simples
Um valor de R$ 5.000,00 é aplicado a uma taxa de 3% ao mês por 10 meses. Qual será o valor dos juros acumulados?
- a) R$ 1.500,00
- b) R$ 1.600,00
- c) R$ 1.550,00
- d) R$ 1.650,00
8. Juros Compostos
Um investimento de R$ 4.000,00 cresce a uma taxa de 1,5% ao mês por 12 meses. Qual será o montante acumulado?
- a) R$ 4.772,19
- b) R$ 4.800,00
- c) R$ 4.760,00
- d) R$ 4.850,00
Gabarito
- b
- a
- b
- a
- c
- a
- a
- a
Esses exercícios cobrem conceitos essenciais de Matemática Financeira e ajudam a fixar o aprendizado.









