A fórmula de Bhaskara é uma das ferramentas matemáticas mais conhecidas e utilizadas em todo o mundo. Comumente usada para resolver equações do segundo grau, sua simplicidade e eficácia tornaram-na um elemento essencial no estudo da matemática. Neste artigo, vamos explorar detalhadamente a origem, aplicações e exemplos práticos da Bhaskara fórmula, além de apresentar dicas para memorizá-la e usá-la corretamente. Se você deseja dominar essa fórmula, continue lendo e descubra tudo sobre ela.
Qual é a Fórmula de Bhaskara?
A fórmula de Bhaskara é uma expressão matemática utilizada para resolver equações quadráticas, que possuem o formato geral:
ax2 + bx + c = 0
onde:
- a, b e c são coeficientes reais, com a ≠0
A expressão da fórmula de Bhaskara é:

onde:
- x representa as raízes da equação,
- Δ = b2 − 4ac é o discriminante, que ajuda a determinar o tipo de raízes da equação.
Essa fórmula permite calcular de maneira direta as soluções para equações do segundo grau, sendo amplamente utilizada em estudos matemáticos, concursos e situações práticas.
O Que É a Fórmula de Bhaskara?
A fórmula de Bhaskara é uma fórmula matemática usada para encontrar as raízes de uma equação quadrática, ou seja, uma equação no formato geral: ax2 + bx + c = 0
onde:
- a, b e c são coeficientes reais, com a≠0
A fórmula é expressa como:
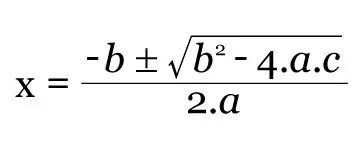
onde:
- x representa as raízes da equação,
Essa fórmula de matemática é amplamente reconhecida por sua versatilidade em resolver problemas complexos.
Fórmula do Delta
O delta é uma parte fundamental da fórmula de Bhaskara e representa o discriminante da equação quadrática. Ele é calculado usando a seguinte fórmula: Δ=b2−4ac\Delta = b^2 – 4ac
O valor de Δ determina o tipo de raízes que a equação terá:
- Se Δ>0: Duas raízes reais e distintas.
- Se Δ=0: Uma raiz real (raízes iguais).
- Se Δ<0: Raízes complexas (não reais).
A fórmula do delta é essencial para entender como aplicar corretamente a fórmula de Bhaskara e interpretar os resultados das equações quadráticas.
Fórmula de Equação Quadrática
A fórmula de equação quadrática é uma aplicação direta da fórmula de Bhaskara. Uma equação quadrática tem o formato: ax2 + bx + c = 0
E suas raízes podem ser encontradas usando a expressão:
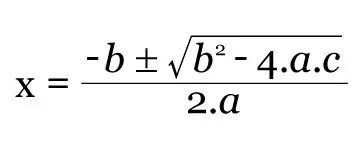
Com a ajuda da fórmula do delta, essa expressão permite resolver qualquer equação quadrática, seja para encontrar suas raízes reais ou complexas. Entender essa relação entre a fórmula da equação quadrática e a fórmula de Bhaskara é crucial para a aplicação eficiente da matemática em problemas do dia a dia.
Origem da Fórmula de Bhaskara
A fórmula leva o nome do matemático indiano Bhaskara Akaria, que viveu no século XII. Embora não tenha sido ele quem desenvolveu originalmente a fórmula, Bhaskara foi responsável por popularizá-la e detalhar sua aplicação em seus escritos matemáticos. Por essa razão, a fórmula de matemática é associada ao seu nome.
Confira também a fórmula de permutação
Como Aplicar a Fórmula de Bhaskara
Para usar a Bhaskara fórmula, siga estes passos:
- Identifique os coeficientes: Certifique-se de que a equação está na forma ax2+bx+c=0. Identifique os valores de a, b e c.
- Calcule o discriminante (Δ): Use a fórmula Δ = b2−4ac
- Substitua os valores na fórmula: Insira os coeficientes e o valor de Δ\Delta na equação x = (−b±Δ)/2.
- Resolva: Encontre os dois valores de x (raízes), considerando os sinais de ±
A compreensão e prática dessa fórmula de matemática são fundamentais para estudantes e profissionais.
Natureza das Raízes
O discriminante (Δ) determina a natureza das raízes da equação:
- Se Δ>0: A equação tem duas raízes reais e distintas.
- Se Δ=0: A equação tem uma única raiz real (raízes iguais).
- Se Δ<0: A equação não possui raízes reais; as raízes são complexas.
Entender essas relações ajuda a aplicar as fórmulas da matemática de maneira mais eficiente.
Exemplos Práticos
Exemplo 1: Resolva a equação 2x2 − 4x − 6 = 02
Identifique os coeficientes: a = 2, b = -4, c = -6.
Calcule o discriminante: Δ=(−4)2 − 4⋅2⋅(−6) = 16+48 = 64
Substitua na fórmula de Bhaskara:
x = (-(-4) ± √64)/2·2
Resolva:
- x1 = (4+8)/4 = 3
- x2 = (4−8)/4 = −1
As raízes são x1 = 3 e x2 = −1
Confira também as fórmulas de geometria plana
Exemplo 2: Resolva a equação x2 − 6x + 9 = 0
- Identifique os coeficientes: a = 1, b = -6, c = 9.
- Calcule o discriminante: Δ = (−6)2 − 4⋅1⋅9 = 36−36 = 0
- Substitua na fórmula de Bhaskara:
x = (-(-6) ± 0)/2 · 1
Resolva:
- x1 = x2 = 3
A equação tem uma raiz dupla: x = 3.
Entre para o nosso Canal do WhatsApp
Dicas para Memorizar a Fórmula de Bhaskara
- Entenda o Contexto: Compreenda como a fórmula é derivada e por que funciona.
- Pratique Regularmente: Resolva muitos exemplos para fixar o procedimento.
- Associe a Palavras-Chave: Crie mnemônicos ou associações para lembrar os componentes da fórmula.
- Visualize: Use diagramas para conectar a fórmula com gráficos de funções quadráticas.
Essas práticas ajudam a internalizar as fórmulas de matemática, tornando-as ferramentas naturais no estudo.
Confira também as formulas geometria espacial
Aplicações
A Bhaskara fórmula é amplamente utilizada em:
- Física: Cálculos relacionados ao movimento parabólico.
- Engenharia: Projeto de estruturas e solução de problemas mecânicos.
- Economia: Modelagem de curvas de oferta e demanda.
- Concursos e Vestibulares: Questões de resolução de equações quadráticas.
A prática constante dessas fórmulas da matemática aumenta a eficiência em resolver problemas complexos.
Se você quer dominar ainda mais a matemática, confira nosso material especial sobre Fórmulas Matemática. Este recurso irá ampliar suas habilidades e facilitar sua jornada nos estudos.
Conclusão
Dominar a Bhaskara fórmula é essencial para qualquer pessoa que estuda matemática. Sua simplicidade e versatilidade fazem dela uma das fórmulas de matemática mais importantes no ensino e na aplicação prática. Com as dicas e exemplos apresentados neste artigo, você está pronto para usar essa poderosa ferramenta em seus estudos e na resolução de problemas.
Baixe nosso eBook gratuito com mais exemplos e explicações detalhadas sobre a fórmula














