A análise combinatória é muito mais do que apenas contar combinações, permutações ou arranjos. Em diversos problemas, surgem condições especiais que desafiam as regras tradicionais, como a distribuição de objetos, a aplicação de restrições ou a necessidade de resolver situações mais complexas. Esses casos especiais exigem criatividade e uma abordagem estratégica para encontrar soluções.
Vamos explorar três categorias de casos especiais: distribuição de objetos em caixas, problemas com restrições e exemplos avançados resolvidos.
📚 Quer aprofundar seus conhecimentos em Análise Combinatória e Probabilidade? Confira nossa recomendação dos melhores livros sobre o tema com exercícios resolvidos e dicas práticas. 👉Os melhores livros de Analise Combinatória e Probabilidade
1. Distribuição de Objetos em Caixas
A distribuição de objetos em caixas é um tema recorrente na análise combinatória. Para resolver esses problemas, é essencial identificar a natureza dos objetos e das caixas: distintos ou idênticos.
Cenários Comuns
1 – Objetos distintos em caixas distintas
Cada objeto pode ser colocado em qualquer caixa, permitindo nk distribuições, onde n é o número de caixas e k o número de objetos.
Exemplo:
Imagine que você tem 3 livros distintos e 2 caixas distintas. Quantas distribuições podem ser feitas?
23 = 8 distribuições
2 – Objetos idênticos em caixas distintas
Aqui, utilizamos a fórmula da combinação com repetição para calcular as possibilidades:
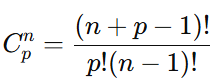
Exemplo:
Distribuir 5 balas idênticas entre 3 crianças.

3 – Objetos distintos em caixas idênticas
Este cenário é mais complexo, pois a distinção das caixas é ignorada. Em geral, requer enumeração ou fórmulas avançadas.
2. Análise Combinatória com Restrições
Problemas com restrições adicionam camadas de complexidade, pois impõem condições que limitam as combinações ou permutações.
Exemplo 1: Agrupamento de Elementos
Quantas maneiras 5 pessoas podem se sentar em uma fila, se duas delas (A e B) devem ficar juntas?
Solução:
Trate A e B como uma única unidade. Isso transforma o problema em 4 “unidades”: (A e B), C, D, E.
As 4 unidades podem ser organizadas de:
4! = 24 maneiras.
Dentro da “unidade” (A e B), eles podem trocar de posição:
2!=2 maneiras.
Total: 24×2 = 48 maneiras
“Quer dominar os cálculos de possibilidades e resolver problemas de contagem com facilidade? Confira nosso artigo completo sobre as Fórmulas da Análise Combinatória e aprenda como aplicá-las no seu dia a dia com exemplos claros e objetivos!
Exemplo 2: Restrições de Exclusão
Quantos números de 4 dígitos podem ser formados usando os números 1, 2, 3, 4 e 5, sem repetir dígitos, e onde o número deve ser ímpar?
Solução:
- O último dígito deve ser ímpar: 1, 3, 5 (3 opções).
- O primeiro dígito pode ser qualquer um dos restantes (4 opções).
- O segundo dígito pode ser escolhido entre os que sobraram (3 opções).
- O terceiro dígito será o restante (2 opções).
Total: 3×4×3×2 = 72 números
3. Exemplos Avançados Resolvidos
Exemplo 1: Distribuição com Condições
Quantas maneiras existem de distribuir 4 presentes distintos entre 3 crianças, de forma que cada criança receba pelo menos um presente?
Solução:
Escolha 1 presente para cada criança (garantindo que todas recebam pelo menos 1):
Número de formas:
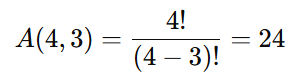
O presente restante pode ser dado a qualquer uma das 3 crianças.
Número de formas: 3
Total: 24×3 = 72 maneiras
Exemplo 2: Formação de Palavras
Quantas palavras diferentes podem ser formadas com as letras da palavra “MASSA”, considerando que as vogais A devem sempre estar separadas?
Solução:
Total de permutações das letras:
Como temos repetições:
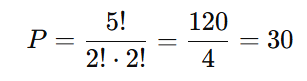
Calcule as palavras onde as vogais A estão juntas:
Trate as duas vogais como uma única unidade, resultando em 4 elementos: (AA), M, S, S.
Total de permutações:
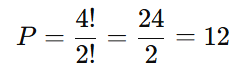
Subtraia as palavras onde as vogais estão juntas das permutações totais:
30 – 12 = 18
Portanto, existem 18 palavras onde as vogais A não estão juntas.
Dicas para Resolver Casos Especiais
- Entenda as Restrições:
Identifique claramente as condições impostas pelo problema. - Divida em Etapas:
Resolva o problema em partes menores, facilitando os cálculos. - Utilize Representações Visuais:
Desenhos, diagramas ou esquemas ajudam a organizar informações.
Quer dominar Análise Combinatória e Probabilidade de forma clara e aprofundada? Adquira já o livro Fundamentos de Matemática Elementar – Volume 5! Essa obra é referência para estudantes e concurseiros, trazendo teoria detalhada, exercícios resolvidos e aplicações práticas que vão turbinar seus estudos. Aproveite para garantir o seu e conquistar o sucesso nas provas!
Conclusão
Os casos especiais na análise combinatória exigem atenção e estratégias personalizadas. Seja na distribuição de objetos, no tratamento de restrições ou em problemas avançados, entender as condições do problema é essencial para aplicar as fórmulas e métodos corretos. Com prática e criatividade, é possível abordar esses desafios de forma eficiente e organizada, transformando problemas complexos em soluções claras indo alem da permutação, do arranjo e da combinação!













