A permutação com repetição é uma variação da permutação na análise combinatória, usada para resolver problemas onde o conjunto de elementos possui itens iguais. Esse conceito é essencial em matemática para calcular o número de arranjos possíveis quando as trocas entre elementos idênticos não resultam em novas combinações únicas.
Neste artigo, vamos explorar o que é a permutação com repetição, como calcular, apresentar exemplos práticos e resolver exercícios detalhados para garantir sua compreensão.

Transforme seus estudos com o eBook Matemática Resumida: + de 90 Mapas Mentais de Matemática! Simplifique conceitos complexos, organize seus estudos e revise de forma prática e eficiente. Baixe agora e conquiste seus objetivos!
O Que é Permutação com Repetição?
Em uma permutação simples, todos os elementos são distintos, e a fórmula P(n)=n!P(n) = n! é aplicada diretamente. Já na permutação com repetição, parte dos elementos se repete, reduzindo o número de combinações únicas.
Por Que Reduzimos as Combinações?
Quando há elementos repetidos, reorganizá-los entre si não cria novas permutações. Por exemplo, na palavra “ANA”, trocar os “A” de posição não gera uma nova palavra distinta.
Fórmula da Permutação com Repetição
A fórmula ajusta o cálculo para levar em conta os elementos repetidos:
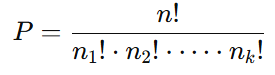
- n: número total de elementos.
- n1, n2, …, nk: números de elementos repetidos para cada tipo.
📚 Quer aprofundar seus conhecimentos em Análise Combinatória e Probabilidade? Confira nossa recomendação dos melhores livros sobre o tema com exercícios resolvidos e dicas práticas. 👉Os melhores livros de Analise Combinatória e Probabilidade
Exemplo Prático 1: Palavra com Letras Repetidas
Quantas palavras diferentes podem ser formadas com as letras da palavra “MASSA”?
Solução:
- Total de letras (n): 5 (M, A, S, S, A).
- Repetições:
- A ocorre 2 vezes (n1 = 2).
- S ocorre 2 vezes (n2 = 2).
Aplicando a fórmula:
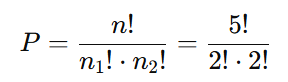
Expandindo os fatoriais:
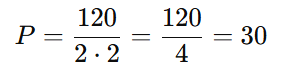
Resposta: Existem 30 palavras diferentes que podem ser formadas com as letras da palavra “MASSA”.
👉Entre no nosso canal do WhatsApp
📘 Todas as fórmulas de matemática em um só lugar! Baixe agora nosso eBook gratuito
Exemplo Prático 2: Balões Coloridos
Quantas sequências diferentes podem ser criadas com 7 balões, sendo 3 azuis, 2 vermelhos e 2 verdes?
Solução:
- Total de balões (n): 7.
- Repetições:
- Azuis (n1 = 3).
- Vermelhos (n2 = 2).
- Verdes (n3 = 2).
Aplicando a fórmula:
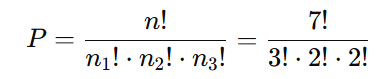
Expandindo os fatoriais:
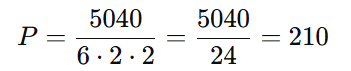
Resposta: Há 210 sequências diferentes de balões.
Passo a Passo para Resolver Permutação com Repetição
1 – Identifique o número total de elementos (n).
Inclua todos os itens no conjunto.
2 – Determine os itens repetidos e suas quantidades (n1, n2, …).
Conte quantas vezes cada item se repete.
3 – Substitua na fórmula:
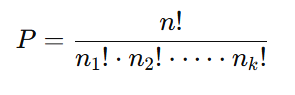
Calcule o resultado.
Aplicações da Permutação com Repetição
A permutação com repetição aparece em várias situações práticas e problemas de matemática. Aqui estão algumas aplicações comuns:
- Criação de Palavras ou Senhas:
Formar palavras com letras repetidas ou senhas com caracteres iguais. - Organização de Itens Repetidos:
Determinar como dispor objetos idênticos em diferentes arranjos. - Planejamento de Cores ou Estilos:
Criar combinações únicas em projetos visuais ou criativos. - Jogos e Problemas de Lógica:
Resolver quebra-cabeças onde elementos repetidos estão presentes.
Exercícios Resolvidos
Exercício 1: Palavras com Letras Repetidas
Quantas palavras diferentes podem ser formadas com as letras da palavra “BANANA”?
Solução:
- Total de letras (n): 6.
- Repetições:
- A ocorre 3 vezes (n1 = 3).
- N ocorre 2 vezes (n2 = 2).
Aplicando a fórmula:
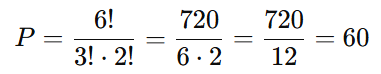
Resposta: Existem 60 palavras diferentes.
Exercício 2: Sequências de Figuras
Quantas sequências diferentes podem ser criadas com 8 figuras, sendo 4 círculos, 2 quadrados e 2 triângulos?
Solução:
- Total de figuras (n): 8.
- Repetições:
- Círculos (n1 = 4).
- Quadrados (n2 = 2).
- Triângulos (n3 = 2).
Aplicando a fórmula:

Resposta: Existem 420 sequências diferentes.
Resumo
A permutação com repetição é um conceito essencial na análise combinatória e amplamente aplicado na resolução de problemas em matemática. Sua fórmula ajusta o cálculo para considerar elementos repetidos, garantindo resultados precisos e eficientes.
Com exemplos claros e exercícios resolvidos, agora você está pronto para aplicar esse conceito em situações práticas e acadêmicas. Que tal resolver mais problemas e explorar a beleza da análise combinatória? A prática é a chave para o aprendizado!









