As Medidas de Tendência Central são ferramentas estatísticas essenciais para resumir um conjunto de dados por meio de um valor representativo. Elas são amplamente utilizadas em diversas áreas do conhecimento, como economia, ciências sociais, educação e saúde, ajudando na interpretação de dados e na tomada de decisões.
Neste artigo, você aprenderá sobre os três principais tipos de medidas de tendência central: média, mediana e moda, incluindo suas fórmulas, explicações detalhadas e exemplos práticos. Vamos lá?

O que são as Medidas de Tendência Central?
As Medidas de Tendência Central representam um conjunto de valores por meio de um número único que expressa o “centro” ou a “tendência” dos dados. São úteis para analisar padrões e comparar grupos de informações.
As três principais medidas são:
- Média Aritmética – Calculada pela soma dos valores dividida pela quantidade total de elementos.
- Mediana – O valor que divide o conjunto ordenado de dados ao meio.
- Moda – O valor mais frequente dentro de um conjunto de dados.
A seguir, exploraremos cada uma delas com exemplos detalhados.
1. Média Aritmética
A média aritmética é a mais utilizada das medidas de tendência central. Ela é obtida somando todos os valores do conjunto e dividindo pelo número total de elementos.
📌 Fórmula:

onde:
- ∑xi é a soma de todos os valores do conjunto,
- n é a quantidade total de elementos.
📌 Exemplo Prático:
As notas de João em uma disciplina foram:
| Nota 1 | Nota 2 | Nota 3 | Nota 4 |
|---|---|---|---|
| 8,7 | 6,3 | 7,1 | 7,9 |
A média aritmética será:
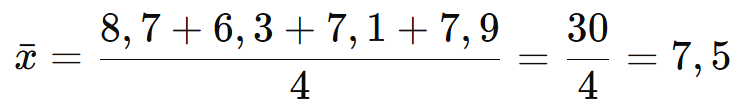
Ou seja, a média das notas de João é 7,5.
📌 Outra Forma de Interpretar a Média
Podemos visualizar a média como um processo de redistribuição dos valores, equilibrando as diferenças entre os dados para encontrar um ponto médio.
2. Média Ponderada
A média ponderada é utilizada quando cada valor do conjunto possui um peso diferente, indicando sua importância relativa.
📌 Fórmula:
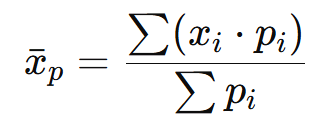
onde:
- xi são os valores dos dados,
- pi são os respectivos pesos,
- ∑pi é a soma dos pesos.
📌 Exemplo Prático:
Se as notas de João tivessem pesos diferentes, conforme a tabela:
| Nota | Peso |
|---|---|
| 8,7 | 1 |
| 6,3 | 2 |
| 7,1 | 3 |
| 7,9 | 4 |
A média ponderada será:
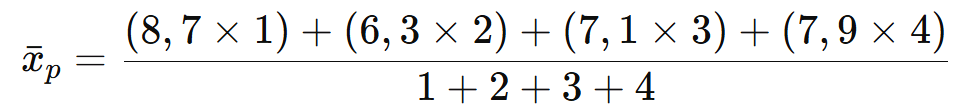
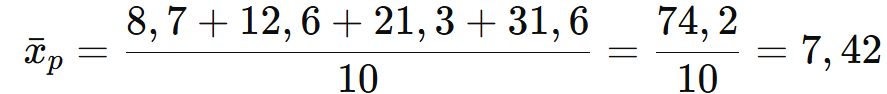
Ou seja, a média ponderada das notas de João é 7,42.
3. Mediana
A mediana é o valor central de um conjunto de dados ordenado. Se a quantidade de elementos for ímpar, a mediana será o valor central. Se for par, a mediana será a média dos dois valores centrais.
📌 Exemplo Prático:
As notas de João foram:
| Nota 1 | Nota 2 | Nota 3 | Nota 4 |
|---|---|---|---|
| 8,7 | 6,3 | 7,1 | 7,9 |
- Ordenamos os valores: 6,3 – 7,1 – 7,9 – 8,7.
- Como há um número par de elementos, a mediana será a média dos dois centrais:
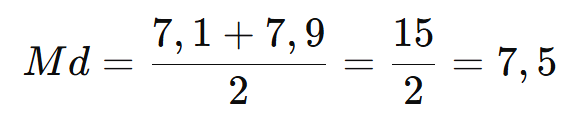
Ou seja, a mediana das notas de João é 7,5.
4. Moda
A moda é o valor que ocorre com maior frequência em um conjunto de dados.
- Amodal: Quando não há repetição de valores.
- Unimodal: Quando há apenas um valor mais frequente.
- Bimodal ou Multimodal: Quando há dois ou mais valores mais frequentes.
📌 Exemplo Prático:
Se João tivesse recebido uma quinta nota e esta fosse 8,7, o conjunto de notas seria:
| Nota 1 | Nota 2 | Nota 3 | Nota 4 | Nota 5 |
|---|---|---|---|---|
| 8,7 | 6,3 | 7,1 | 7,9 | 8,7 |
A nota 8,7 aparece com mais frequência, então a moda seria:
Mo = 8,7
5. Média Geométrica
A média geométrica é utilizada quando queremos calcular uma média proporcional entre valores, sendo amplamente aplicada em taxas de crescimento, como economia e biologia.
📌 Fórmula:
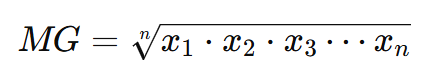
onde:
- x1, x2, x3, …, xn são os valores do conjunto,
- n é a quantidade total de elementos.
📌 Exemplo Prático:
Se os rendimentos anuais de um investimento foram 5%, 10% e 15%, a média geométrica será:

Convertendo para percentual: 9,8%.
Ou seja, o crescimento médio anual foi de 9,8%.
📊 6. Média Harmônica
A média harmônica é usada quando trabalhamos com taxas, velocidades ou razões, sendo particularmente útil em problemas de movimento e eficiência.
📌 Fórmula:
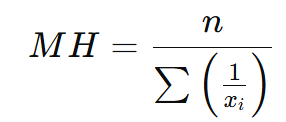
onde:
- n é a quantidade total de elementos,
- xi são os valores do conjunto.
📌 Exemplo Prático:
Três máquinas produzem 10, 15 e 20 peças por hora. Qual é a produção média considerando a taxa de cada uma?
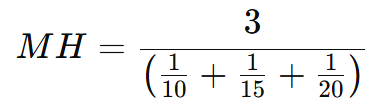
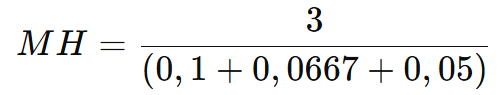
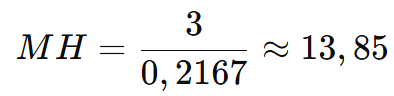
Ou seja, a produção média por hora das máquinas é 13,85 peças.
🎯 Conclusão Atualizada
Além das principais medidas de tendência central (média, mediana e moda), as médias geométrica e harmônica oferecem alternativas valiosas para contextos específicos, como crescimento exponencial e análise de taxas.
✅ Resumo das médias abordadas:
| Medida | Como calcular | Quando usar |
|---|---|---|
| Média Aritmética | Soma dos valores ÷ total de elementos | Dados homogêneos |
| Média Ponderada | Média levando em conta pesos | Quando os valores têm importância diferente |
| Mediana | Valor central do conjunto ordenado | Conjuntos com valores extremos |
| Moda | Valor mais frequente | Identificação de padrões |
| Média Geométrica | Raiz do produto dos valores | Taxas de crescimento |
| Média Harmônica | Média do inverso dos valores | Taxas e velocidades |
Agora que você aprendeu todas as medidas de tendência central, compartilhe este artigo para ajudar mais pessoas a entender estatística de forma clara e objetiva! 📊✅
🎯 Aplicação das Medidas de Tendência Central no ENEM
Vejamos um exemplo de questão do ENEM 2019 envolvendo mediana:
📌 Questão:
Os alunos de uma turma foram divididos em dois grupos para jogar basquete e futebol. O grupo de basquete tem uma pessoa a mais e é formado pelos alunos mais altos. As alturas dos alunos são:
| Aluno | Altura (m) |
|---|---|
| P | 1,65 |
| J | 1,66 |
| F | 1,67 |
| M | 1,68 |
Sabemos que a mediana é 1,67 e que ela representa um jogador de basquete. Assim, os alunos que jogam futebol são os de alturas 1,65 m e 1,66 m, e os que jogam basquete são os de alturas 1,67 m e 1,68 m.
✅ Alternativa correta: C) futebol, futebol, basquete, basquete.
🎯 Conclusão
As medidas de tendência central são fundamentais para a análise de dados, auxiliando na compreensão de padrões e facilitando a tomada de decisões em diversas áreas.
✅ Resumo das medidas estudadas:
| Medida | Como calcular | Quando usar |
|---|---|---|
| Média | Soma dos valores ÷ total de elementos | Dados homogêneos |
| Média ponderada | Média levando em conta pesos | Quando os valores têm importância diferente |
| Mediana | Valor central do conjunto ordenado | Conjuntos com valores extremos |
| Moda | Valor mais frequente | Identificação de padrões |
Agora que você aprendeu tudo sobre medidas de tendência central, compartilhe este artigo com quem precisa entender estatística de forma simples e prática! 🎯📊
Este artigo é bem completo, didático e otimizado para SEO. Caso queira alguma adaptação, me avise! 😊

























