Os números inteiros fazem parte do nosso cotidiano e têm grande relevância em diversos contextos matemáticos. Neste artigo, vamos explorar o que são números inteiros, suas operações, propriedades e aplicações. Além disso, veremos exemplos práticos para reforçar o entendimento.
1. O Que São Números Inteiros?
Os números inteiros são um conjunto de números que incluem os números positivos, os números negativos e o zero. Esse conjunto é representado por ( \mathbb{Z} ) e pode ser expresso da seguinte maneira:
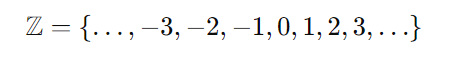
Os números inteiros abrangem:
- Números inteiros positivos: ( 1, 2, 3, …)
- Números inteiros negativos: ( -1, -2, -3, …)
- Zero: É o número neutro entre os positivos e negativos.
2. Representação na Linha Numérica
Os números inteiros podem ser facilmente representados em uma linha numérica, onde os números positivos estão à direita do zero e os números negativos à esquerda.
… -3, -2, -1, 0, 1, 2, 3, …
Essa representação é útil para comparar números inteiros e para entender a relação entre números positivos e negativos.
3. Operações com Números Inteiros
3.1 Adição de Números Inteiros
A adição de números inteiros segue regras simples:
- Somar dois números positivos resulta em um número positivo.
- Somar dois números negativos resulta em um número negativo.
- Quando somamos um número positivo e um número negativo, subtraímos o valor absoluto menor do valor absoluto maior e mantemos o sinal do número de maior valor absoluto.
Exemplo:
(-5) + 3 = -2
Neste caso, subtraímos o valor absoluto de 3 de 5, resultando em 2. O sinal negativo permanece, pois 5 é maior que 3.
3.2 Subtração de Números Inteiros
A subtração de números inteiros pode ser vista como a adição do oposto:
a – b = a + (-b)
Ou seja, subtrair um número é o mesmo que adicionar o seu oposto.
Exemplo:
7 – (-3) = 7 + 3 = 10
3.3 Multiplicação de Números Inteiros
A multiplicação de números inteiros segue regras de sinais:
- O produto de dois números positivos é positivo.
- O produto de dois números negativos também é positivo.
- O produto de um número positivo e um número negativo é negativo.
Exemplo:
(-4) x 6 = -24
3.4 Divisão de Números Inteiros
A divisão de números inteiros segue as mesmas regras de sinais da multiplicação:
- A divisão de dois números com o mesmo sinal resulta em um número positivo.
- A divisão de dois números com sinais diferentes resulta em um número negativo.
Exemplo:
(-12)/ 4 = -3
4. Propriedades dos Números Inteiros
Os números inteiros possuem várias propriedades importantes:
4.1 Propriedade Comutativa
A adição e a multiplicação de números inteiros são comutativas, ou seja, a ordem dos números não altera o resultado:
a + b = b + a
a x b = b x a
4.2 Propriedade Associativa
A adição e a multiplicação de números inteiros também são associativas, o que significa que a maneira como agrupamos os números não altera o resultado:
(a + b) + c = a + (b + c)
(a x b) x c = a x (b x c)
4.3 Propriedade Distributiva
A multiplicação distribui-se sobre a adição e a subtração:
a x (b + c) = (a x b) + (a x c)
4.4 Oposto de um Número Inteiro
O oposto de um número inteiro ( a ) é o número ( -a ), e a soma de ( a ) com seu oposto é zero:
a + (-a) = 0
5. Módulo de um Número Inteiro
O módulo ou valor absoluto de um número inteiro é a distância do número até o zero na linha numérica, desconsiderando o sinal.
- O módulo de um número ( a ) é representado por ( |a| ).
- Se ( a ) for positivo ou zero, ( |a| = a ). Se ( a ) for negativo, ( |a| = -a ).
Eemplo:
| -7 | = 7
| 5 | = 5
6. Aplicações dos Números Inteiros no Cotidiano
Os números inteiros são amplamente usados em situações do dia a dia, como:
- Temperatura: Quando falamos de temperaturas negativas, como −5∘C, estamos utilizando números inteiros.
- Finanças: Saldos negativos em contas bancárias, representados por dívidas.
- Altura: Altura abaixo do nível do mar, como ( -200 ) metros.
7. Exemplos e Exercícios de Números Inteiros
Exercício 1: Adição e Subtração
Calcule:
(-8) + 4 – (-3)
Solução:
(-8) + 4 = -4
-4 – (-3) = -4 + 3 = -1
Resposta: ( -1 )
Exercício 2: Multiplicação
Calcule:
(-6) x (-2) x 3
Solução:
(-6) x (-2) = 12
12 x 3 = 36
Resposta: ( 36 )
Exercício 3: Módulo
Calcule o valor absoluto de ( -15 ) e ( 9 ).
| -15 | = 15 e | 9 | = 9
8. História dos Números Inteiros
A inclusão de números negativos no campo da matemática nem sempre foi aceita. Os números inteiros negativos começaram a ser reconhecidos pelos matemáticos na China e na Índia muitos séculos antes de serem aceitos na Europa. A aceitação completa dos números inteiros veio com o desenvolvimento da álgebra e a necessidade de resolver equações que envolviam resultados negativos.
Conclusão
Os números inteiros desempenham um papel essencial na matemática e no cotidiano. Compreender suas propriedades, operações e aplicações é fundamental para o aprendizado da matemática básica e para a resolução de problemas práticos. A prática com exercícios ajuda a fixar o conteúdo e a desenvolver habilidades para o uso dos números inteiros em diversos contextos.
Espero que este artigo ajude a esclarecer os principais aspectos sobre números inteiros!
Conjuntos Numéricos: Exercícios com Soluções Detalhadas
Lista de Exercícios Resolvidos sobre Números Inteiros: Operações e Propriedades
Exercício 01 – Lembrando que -1 é o oposto de 1, responda:
a) Qual é a soma de dois números opostos?
b) Qual é o oposto de 3?
c) Qual é o oposto de -4?
d) Qual é o oposto de 0?
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
a) 0
b) -3
c) 4
d) 0
[/toggle]
Exercício 02 – Indica-se o valor absoluto de n por |n| (lê-se: “módulo de n“ ou “valor absoluto de n”).
Determine o valor de:
a) |8| 8
b) |-8| 8
c) |-5|5
d) |5| 5
e) |0| 0
f) |-(-1)| 1
g) 2 x |-5| – |3| 7
h) |-6| + | 2 – (9 – 3) + 1| 9
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
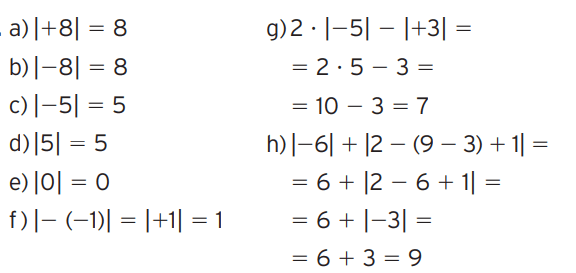
[/toggle]
Exercício 02 – Analise a sucessão numérica abaixo e responda às perguntas:
1, -2, 3, -4, 5, -6, 7, -8, 9, -10, 11, …
a) Qual é o vigésimo quinto número dessa sequência?
b) Qual é a soma dos dois primeiros números? E a dos dois seguintes?
c) Qual é a soma dos 25 primeiros números?
d) Qual é o quinquagésimo número dessa sequência?
e) Qual é a soma dos 50 primeiros números?
f) Qual é o sinal do produto dos 25 primeiros números?
g) Qual é o sinal do produto dos 50 primeiros números?
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]


[/toggle]













