A equação do segundo grau é uma das ferramentas mais importantes em matemática, especialmente em álgebra. Neste artigo, exploraremos a equação canônica da função do segundo grau, que nos permite entender melhor a posição e a forma da parábola associada a essa função.
O que é a Equação Canônica?
A equação canônica de uma função do segundo grau, também conhecida como equação na forma de vértice, é dada por:

Aqui:
- a determina a concavidade da parábola. Se ( a > 0 ), a parábola é côncava para cima; se ( a < 0 ), é côncava para baixo.
- (xv, yv) são as coordenadas do vértice da parábola, o ponto onde ela atinge seu valor máximo ou mínimo.
A forma canônica é útil porque nos dá uma visão direta da localização do vértice da parábola, o que facilita a análise gráfica.
Passos para Encontrar a Equação Canônica
Dada uma função do segundo grau na forma geral y = ax2 + bx + c, siga estes passos para convertê-la na forma canônica:
- Calcule ( xv ), a coordenada x do vértice:
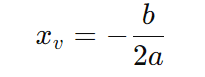
- Calcule ( yv ), substituindo ( x_v ) na equação original:
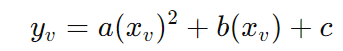
- Escreva a equação na forma canônica usando a, xv e yv.
Exemplo 1: Convertendo para a Forma Canônica
Considere a função quadrática:
y = 2x2 – 8x + 6
Passo 1: Calcule ( xv )
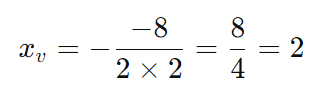
Passo 2: Calcule ( yv )
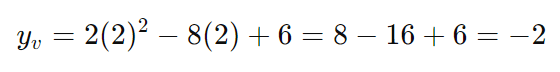
Passo 3: Escreva a equação na forma canônica
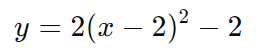
A equação canônica é y = 2(x – 2)2 – 2, indicando que a parábola tem seu vértice em (2, -2) e é côncava para cima.
Exemplo 2: Interpretação Gráfica
Para a função:
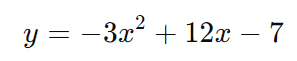
Passo 1: Calcule ( xv )
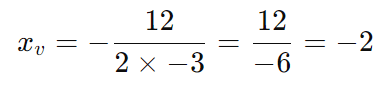
Passo 2: Calcule ( yv )
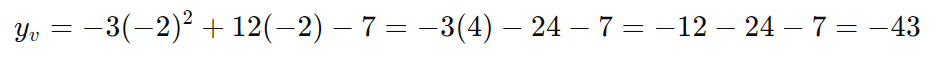
Passo 3: Escreva a equação na forma canônica
y = -3(x + 2)2 – 43
Essa parábola tem o vértice em (-2, -43) e é côncava para baixo.
Exercícios Resolvidos
Exercício 1:
Dada a função y = 4x2 – 16x + 7, encontre a equação na forma canônica.
Solução:
- Calcule xv:
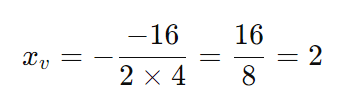
- Substitua em yv:
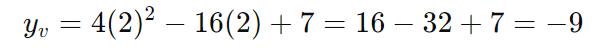
- Escreva a equação:
- y = 4(x – 2)2 – 9
Exercício 2:
Encontre o vértice e a concavidade da função y = -5x2 + 20x – 15.
Solução:
- Calcule xv:
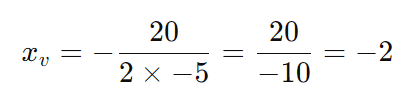
- Calcule ( yv ):
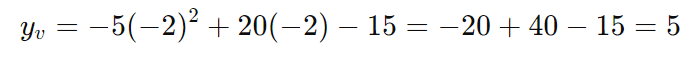
- Escreva a equação:
- y = -5(x + 2)2 + 5
A parábola é côncava para baixo, com vértice em (-2, 5).
Conclusão
A forma canônica da função do segundo grau é uma ferramenta poderosa para analisar as características da parábola, como seu vértice e concavidade. Com a prática, você conseguirá facilmente converter funções quadráticas e interpretar seus gráficos. Utilize os exemplos e exercícios resolvidos para aprofundar sua compreensão e domínio do tema.























