A função logarítmica é uma das funções matemáticas mais importantes e versáteis, amplamente utilizada em diversas áreas da matemática, ciências e engenharias. Ela é a inversa da função exponencial e está intimamente relacionada a conceitos como crescimento e decaimento exponencial, escalas logarítmicas, e é fundamental em cálculos que envolvem multiplicações, divisões, e potências. Este artigo abordará a definição, propriedades, gráficos, e aplicações da função logarítmica, com exemplos detalhados para facilitar a compreensão.
Definição da Função Logarítmica
A função logarítmica é definida como a função inversa da função exponencial. Se temos uma função exponencial y = ax ou f(x) = ax, onde a>0 e a ≠ 1 , então a função logarítmica é dada por:
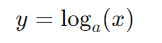
Aqui, y=loga(x) significa que x=ay. Em outras palavras, y é o expoente ao qual a base a deve ser elevada para resultar em x.
Por exemplo, se a=2 e x=8, então log2(8)=3 porque 23=8.
Propriedades dos Logaritmos
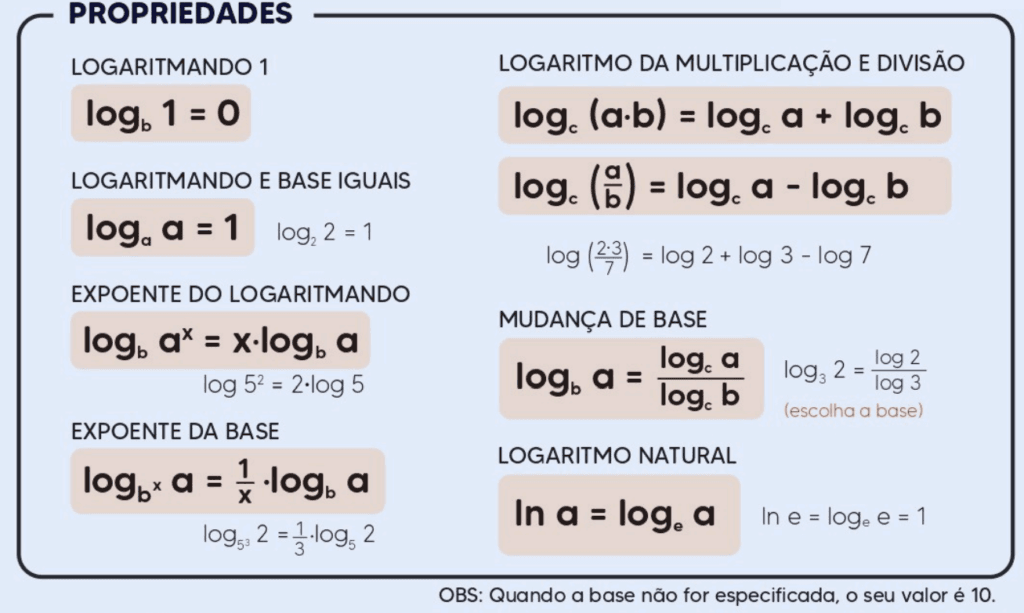
Os logaritmos possuem diversas propriedades importantes que facilitam a simplificação e resolução de problemas matemáticos. As principais propriedades são:
- Propriedade do Produto: A propriedade do produto dos logaritmos estabelece que o logaritmo de um produto de dois números é igual à soma dos logaritmos desses números, ambos com a mesma base. Em outras palavras, para uma base a, a propriedade pode ser expressa como:
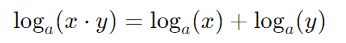
Essa propriedade é útil quando precisamos calcular logaritmos em uma base para a qual não temos uma tabela ou calculadora disponível.
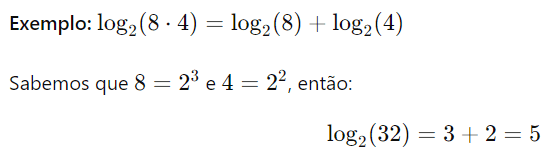
- Propriedade do Quociente: A propriedade do quociente dos logaritmos afirma que o logaritmo de um quociente entre dois números é igual à diferença entre os logaritmos desses números, ambos com a mesma base. Formalmente, para uma base aaa, essa propriedade é expressa como:
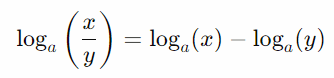
Essa propriedade é útil para simplificar expressões logarítmicas e resolver equações envolvendo divisões.
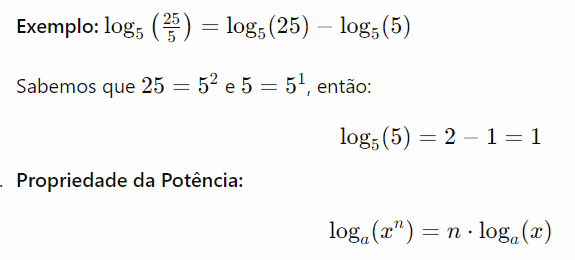
Propriedade da Potência: A propriedade da potência dos logaritmos estabelece que o logaritmo de um número elevado a um expoente é igual ao produto do expoente pelo logaritmo do número, ambos com a mesma base. Em termos formais, para uma base a, essa propriedade é dada por:
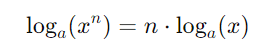
Essa propriedade facilita o processo de simplificação de expressões logarítmicas, especialmente quando lidamos com potências.
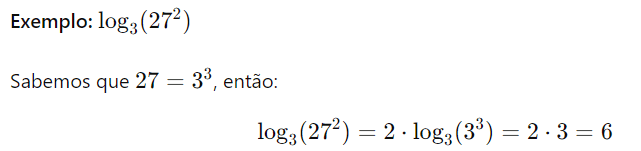
- Propriedade da Raiz: A propriedade da raiz dos logaritmos afirma que o logaritmo de uma raiz n-ésima de um número é igual ao logaritmo desse número dividido por n, ambos com a mesma base. Formalmente, para uma base a, essa propriedade pode ser expressa como:
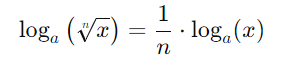
Essa propriedade é útil para simplificar expressões logarítmicas que envolvem raízes.
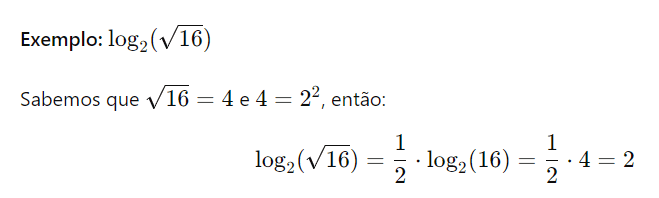
- Mudança de Base: A propriedade da mudança de base dos logaritmos permite calcular o logaritmo de um número em uma base diferente da original. Ela afirma que o logaritmo de um número x na base a pode ser expresso como a razão entre o logaritmo de x e o logaritmo de a em uma nova base b. Formalmente, a propriedade é dada por:
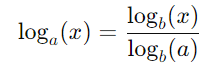
Essa propriedade é útil quando precisamos calcular logaritmos em uma base para a qual não temos uma tabela ou calculadora disponível.

Gráficos da Função Logarítmica
O gráfico de uma função logarítmica y=loga(x) tem algumas características distintas:
- Domínio e Imagem:
- O domínio da função logarítmica y=loga(x) é x>0 e x ≠ 0 (conjunto dos números reais positivos, excluindo o zero).
- A imagem é o conjunto de todos os números reais.
- Intersecção com o Eixo X:
- A função logarítmica sempre intersecta o eixo x em x=1, pois loga(1)=0 para qualquer base a>0.
- Comportamento para Diferentes Bases:
- Se 0<a<1, a função logarítmica é decrescente.
- Se a>1, a função logarítmica é crescente.
- Assíntota Vertical:
- O gráfico possui uma assíntota vertical em x=0, pois loga(x) tende a −∞ à medida que x se aproxima de zero pela direita.
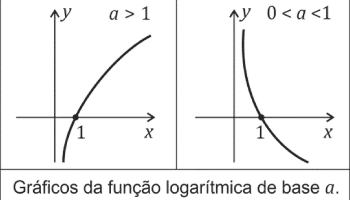
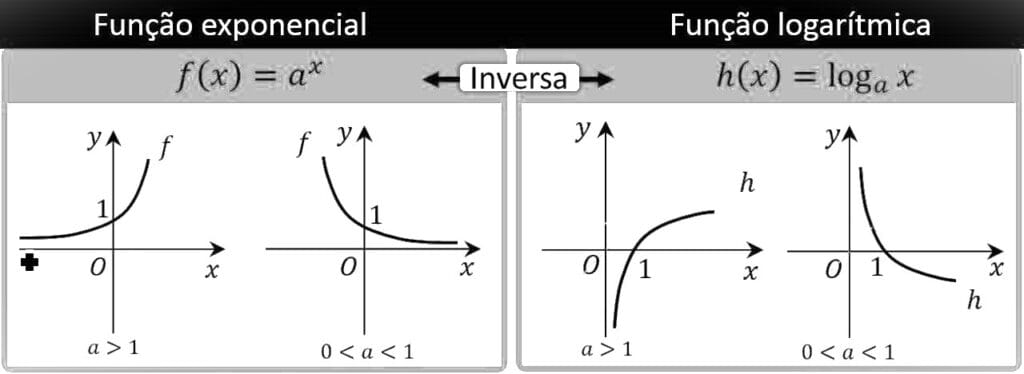
A relação entre o gráfico da Função Exponencial e a Função Logarítmica