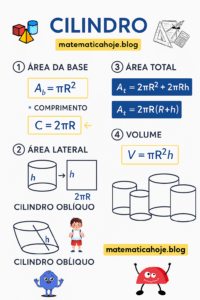
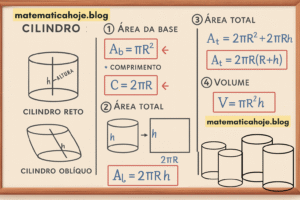
A parábola é uma curva plana que resulta da interseção de um plano paralelo a uma geratriz de um cone com a superfície cônica. É um dos tipos de seções cônicas, junto com a elipse e a hipérbole. As propriedades geométricas e analíticas da parábola a tornam uma importante ferramenta em diversas áreas da matemática e da física.
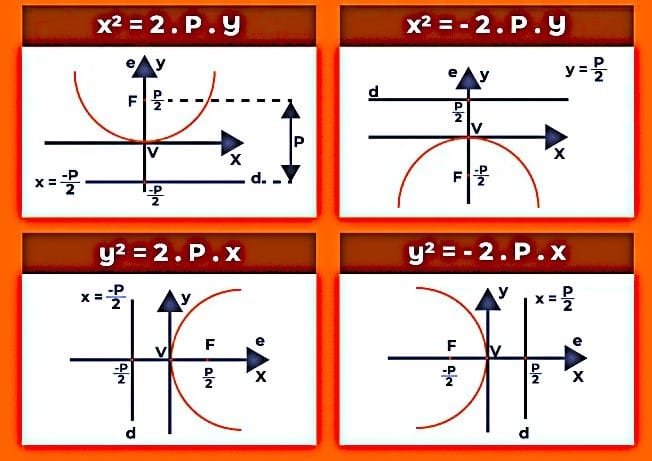
1. Definição e Elementos da Parábola
Uma parábola pode ser definida como o conjunto de todos os pontos P(x, y) do plano que estão à mesma distância de um ponto fixo, chamado foco ( F ), e de uma reta fixa, chamada diretriz ( D ).
Os principais elementos de uma parábola incluem:
- Vértice ( V ): O ponto onde a parábola muda de direção, sendo o ponto médio entre o foco e a diretriz.
- Foco ( F ): Um ponto fixo que, juntamente com a diretriz, define a parábola.
- Diretriz ( D ): Uma reta fixa que, juntamente com o foco, define a parábola.
- Eixo de simetria: A reta que passa pelo foco e pelo vértice, dividindo a parábola em duas partes simétricas.
- Lado reto: O segmento de reta que passa pelo foco e é perpendicular ao eixo de simetria. Seu comprimento é ( 4p ), onde ( p ) é a distância do vértice ao foco.
2. Equação da Parábola com Vértice na Origem O(0, 0)
Considerando uma parábola com vértice na origem O(0, 0) e foco em F(0, p), a equação da parábola pode ser dada de duas formas, dependendo da orientação do eixo de simetria:
a. Parábola com Eixo de Simetria Vertical
Se o eixo de simetria é vertical, a parábola pode abrir para cima ou para baixo. A equação é:
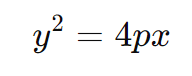
- ( p > 0 ): A parábola abre para cima.
- ( p < 0 ): A parábola abre para baixo.
b. Parábola com Eixo de Simetria Horizontal
Se o eixo de simetria é horizontal, a parábola pode abrir para a direita ou para a esquerda. A equação é:
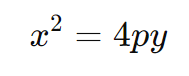
- ( p > 0 ): A parábola abre para a direita.
- ( p < 0 ): A parábola abre para a esquerda.
3. Equação da Parábola com Vértice em O(x0, y0)
Quando a parábola tem o vértice deslocado para (x0, y0), as equações se ajustam da seguinte forma:
a. Parábola com Eixo de Simetria Vertical
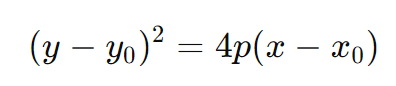
b. Parábola com Eixo de Simetria Horizontal
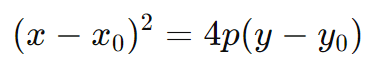
4. Características da Parábola
a. Diretriz e Foco
- Para a equação ( y2 = 4px ), a diretriz é ( x = -p ) e o foco é F(p, 0).
- Para a equação ( x2 = 4py ), a diretriz é ( y = -p ) e o foco é F(0, p).
b. Lado Reto
O comprimento do lado reto, que passa pelo foco e é perpendicular ao eixo de simetria, é dado por 4p.
c. Abertura da Parábola
A abertura da parábola é inversamente proporcional ao valor de p. Quanto maior o valor absoluto de p, mais “aberta” é a parábola. Quanto menor o valor absoluto de ( p ), mais “fechada” é a parábola.
5. Exemplos Resolvidos
Exemplo 1: Encontre a equação de uma parábola com vértice na origem (0, 0) e foco em F(0, 3).
Solução:
Aqui, p = 3 e o eixo de simetria é vertical. Portanto, a equação da parábola é:
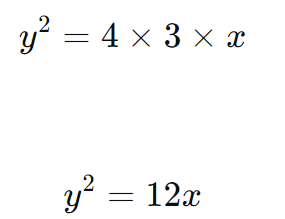
Exemplo 2: Encontre a equação de uma parábola com vértice em (1, 2) e foco em F(5, 2).
Solução:
Aqui, o eixo de simetria é horizontal, e a distância p é 4 (pois a distância entre (1, 2) e (5, 2) é 4). Portanto, a equação da parábola é:
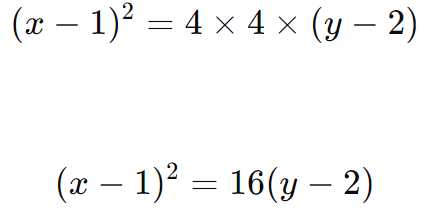
6. Aplicações da Parábola
As parábolas têm várias aplicações práticas. Algumas delas incluem:
- Refletores e Antenas: A forma parabólica é utilizada em refletores de luz e em antenas parabólicas para focar ou dispersar ondas de rádio e luz de maneira eficiente.
- Arquitetura: Estruturas parabólicas são usadas em arquitetura por sua resistência e capacidade de distribuir forças.
- Trajetórias de Projéteis: O movimento de projéteis sob a ação da gravidade segue uma trajetória parabólica, sendo uma aplicação direta das equações da parábola.
Conclusão
A parábola é uma das curvas matemática mais estudadas em geometria e álgebra, com propriedades que a tornam útil em uma ampla gama de aplicações, desde a física até a engenharia e a arquitetura. Compreender suas equações e características permite explorar suas inúmeras aplicações práticas e teóricas.
Leia também
Geometria Analítica: Pontos ⇒ Distância, Ponto Médio e Colinearidade
Distância entre Retas e Cálculo da Área de um Triângulo
Circunferência: Equação Geral e Reduzida
A Parábola: Definição, Propriedades e Equações