Análise combinatória é um ramo da matemática que estuda a contagem, a combinação e a disposição dos elementos de um conjunto. Essa área é fundamental para a resolução de problemas de probabilidade e estatística, com aplicações vastas que vão desde a criação de senhas até a análise de dados genéticos. Neste artigo, exploraremos os principais conceitos da análise combinatória, incluindo o princípio multiplicativo, fatorial, combinações, arranjos e permutações, acompanhados de exemplos detalhados.
1. Princípio Multiplicativo
Utilizado para calcular o número total de possibilidades em uma sequência de escolhas independentes. Se um evento pode ocorrer de m maneiras e outro de n maneiras, o total de combinações possíveis é o produto dessas quantidades.
Fórmula:
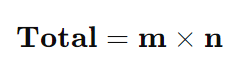
Exemplo 1:
Imagine que você tenha 3 camisetas e 2 calças. Quantos conjuntos diferentes de roupas você pode formar?
- Camisetas: 3 opções (A, B, C)
- Calças: 2 opções (X, Y)
O número total de combinações possíveis é 3×2=63 \times 2 = 63×2=6. As combinações possíveis são: (A,X), (A,Y), (B,X), (B,Y), (C,X), (C,Y).
Exemplo 2:
Suponha que você tenha 4 modelos de carros e 3 cores disponíveis. Quantas combinações diferentes de modelo e cor você pode escolher?
- Modelos: 4 opções (M1, M2, M3, M4)
- Cores: 3 opções (C1, C2, C3)
O número total de combinações é 4×3=12. As combinações possíveis são: (M1,C1), (M1,C2), (M1,C3), (M2,C1), (M2,C2), (M2,C3), (M3,C1), (M3,C2), (M3,C3), (M4,C1), (M4,C2), (M4,C3).
2. Fatorial
Representa o produto de todos os números inteiros positivos de 1 até n. É usado para calcular o número total de maneiras de organizar n objetos distintos.
Fórmula:
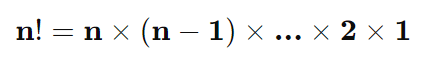
Exemplo 1:
Calcule o fatorial de 5.
5!=5×4×3×2×1=120
Exemplo 2:
Calcule o fatorial de 7.
7!=7×6×5×4×3×2×1=5040
3. Combinação Simples
Refere-se à seleção de k elementos de um conjunto de n elementos, onde a ordem dos elementos não importa. Usado para problemas onde a disposição não é relevante.
Fórmula:
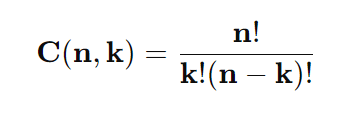
Exemplo 1:
De um grupo de 5 pessoas, quantas equipes de 3 pessoas podem ser formadas?
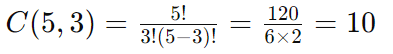
Exemplo 2:
Quantas duplas podem ser formadas a partir de um grupo de 4 pessoas?
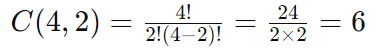
4. Combinação com Elementos Repetidos
Similar à combinação simples, mas permite que os elementos sejam repetidos na seleção. É útil quando há repetição permitida entre os elementos escolhidos.
Fórmula:
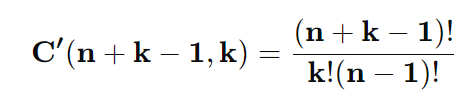
Exemplo 1: Quantas combinações de 3 elementos podem ser formadas a partir de um conjunto de 2 elementos (A, B), com repetição?
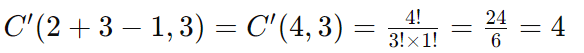
As combinações são: (A,A,A), (A,A,B), (A,B,B), (B,B,B).
Exemplo 2:
Quantas maneiras diferentes existem para escolher 4 bolas de cores diferentes de uma caixa contendo bolas de 3 cores diferentes, permitindo repetição?
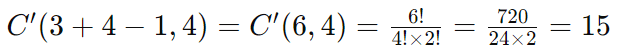
5. Arranjo Simples
Trata da disposição de k elementos de um conjunto de n elementos, onde a ordem importa. É aplicado em situações onde a sequência ou posição dos elementos é relevante.
Fórmula:
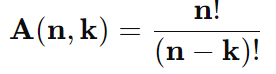
Exemplo 1: Quantos arranjos de 2 letras podem ser formados a partir das letras A, B e C?
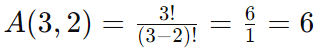
Os arranjos são: AB, AC, BA, BC, CA, CB.
Exemplo 2:
De quantas maneiras diferentes podem ser organizados 3 livros em uma prateleira com 5 espaços?
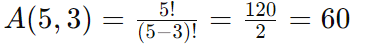
6. Arranjo com Elementos Repetidos
Semelhante ao arranjo simples, mas permite que os elementos sejam repetidos. Usado para contar disposições quando a repetição é permitida.
Fórmula:
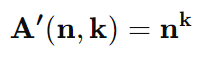
Exemplo 1:
Quantos números de 2 dígitos podem ser formados usando os dígitos 1 e 2, permitindo repetição?
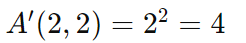
Os números são: 11, 12, 21, 22.
Exemplo 2:
Quantas senhas de 3 caracteres podem ser formadas com as letras A, B e C, permitindo repetição?
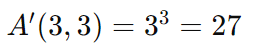
7. Permutação Simples
Refere-se à disposição de todos os elementos de um conjunto, onde a ordem é importante. É utilizado para calcular o número de maneiras diferentes de organizar um conjunto de n elementos distintos.
Fórmula:
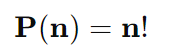
Exemplo 1:
Quantas maneiras diferentes existem para organizar as letras da palavra “AMOR”?
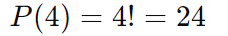
Exemplo 2:
Quantas maneiras diferentes existem para organizar as letras da palavra “LIVRO”?
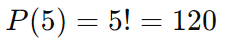
8. Permutação com Elementos Repetidos
Como a permutação simples, mas aplicada quando há elementos repetidos no conjunto. É usada para determinar as possíveis disposições levando em conta as repetições.
Fórmula:
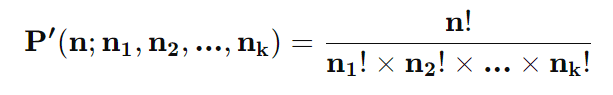
Exemplo 1:
Quantas maneiras diferentes existem para organizar as letras da palavra “BALA”, considerando a repetição da letra A?
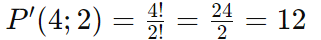
Exemplo 2:
Quantas maneiras diferentes existem para organizar as letras da palavra “MAMA”, considerando a repetição das letras M e A?
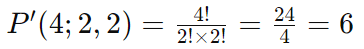
9. Permutação Circular
A permutação circular é usada quando os elementos são organizados em um círculo. Usada para contar as maneiras de organizar elementos em um círculo, onde a ordem é importante, mas rotações são consideradas equivalentes. A disposição circular difere da linear pois o ponto de partida é irrelevante.
Fórmula:
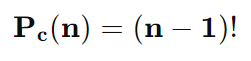
Exemplo 1:
Quantas maneiras diferentes existem para organizar 4 pessoas ao redor de uma mesa redonda?
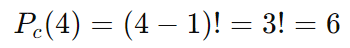
Exemplo 2:
Quantas maneiras diferentes existem para organizar 5 pessoas em uma roda gigante com 5 assentos?
Esses conceitos e exemplos fornecem uma base sólida para entender a análise combinatória. A compreensão desses princípios é fundamental para resolver problemas complexos em várias áreas, incluindo ciência da computação, estatística e engenharia.
Lista de exercício Analise Combinatória
1 – Você tem 5 camisas e 3 calças. Quantos conjuntos diferentes de roupa podem ser formados?
A) 8
B) 15
C) 10
D) 18
2 – Qual é o valor de 6!?
A) 120
B) 720
C) 360
D) 5040
3 – De um grupo de 7 pessoas, quantas comissões de 3 pessoas podem ser formadas?
A) 21
B) 35
C) 15
D) 28
4 – Quantas combinações de 4 bolas podem ser formadas a partir de um conjunto de 3 bolas de cores diferentes, com repetição?
A) 10
B) 15
C) 20
D) 35
5 – De quantas maneiras diferentes podem ser organizados 4 livros em uma prateleira com 5 livros disponíveis?
A) 60
B) 120
C) 240
D) 360
6 – Quantos números de 3 dígitos podem ser formados usando os dígitos 1, 2 e 3, permitindo repetição?
A) 6
B) 9
C) 27
D) 12
7 – Quantas maneiras diferentes existem para organizar as letras da palavra “CASA”?
A) 12
B) 24
C) 16
D) 20
8 – Quantas maneiras diferentes existem para organizar as letras da palavra “BANANA”?
A) 60
B) 120
C) 720
D) 360
9 – Quantas maneiras diferentes existem para organizar 5 pessoas ao redor de uma mesa redonda?
A) 24
B) 120
C) 12
D) 36
10 – De um grupo de 6 alunos, quantas duplas podem ser formadas, e de quantas maneiras diferentes essas duplas podem ser organizadas em uma fila?
A) 15 combinações e 120 arranjos
B) 15 combinações e 720 arranjos
C) 30 combinações e 120 arranjos
D) 30 combinações e 720 arranjos
Gabarito:
1 – B
2 – B
3 – B
4 – B
5 – A
6 – C
7 – B
8 – D
9 – A
10 – B













