(CESPE / CEBRASPE 2024 – ITAIPU BINACIONAL – Função: Advogado)
Certa usina hidrelétrica possui cinco unidades geradoras de energia que funcionam independentemente umas das outras.
Na situação hipotética CB2A3-II, se três unidades geradoras tiverem de ser paradas em certo dia para manutenção, a quantidade de maneiras que a direção da usina poderá escolher para definir as unidades que ficarão paradas será igual a
A) 125.
B) 60.
C) 15.
D) 10.
E) 8.
Para resolver essa questão, precisamos calcular de quantas maneiras diferentes é possível escolher 3 unidades geradoras para serem paradas, dentre as 5 disponíveis. Como a ordem de escolha não importa, trata-se de um problema de combinação.
A fórmula para calcular o número de combinações de n elementos tomados k a k é dada por:
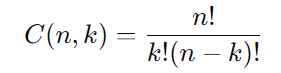
No problema, temos n=5 (as 5 unidades geradoras) e k=3 (as 3 unidades que devem ser paradas). Substituindo esses valores na fórmula:
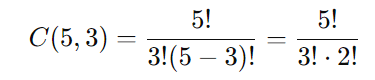
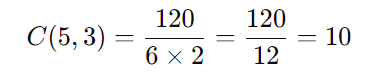
Portanto, a quantidade de maneiras que a direção da usina poderá escolher para definir as unidades que ficarão paradas é 10.
A alternativa correta é:
D) 10.











