O coeficiente de variação (CV) é uma ferramenta essencial na matemática aplicada à análise estatística, utilizada para medir a dispersão de um conjunto de dados em relação à sua média. Diferentemente de outras medidas de dispersão, como a variância e o desvio padrão, o CV é expresso em porcentagem, tornando-se particularmente vantajoso para comparar a variabilidade entre diferentes conjuntos de dados, independentemente das unidades de medida ou das magnitudes das médias.
Como Calcular o Coeficiente de Variação
A fórmula para calcular o coeficiente de variação é simples:
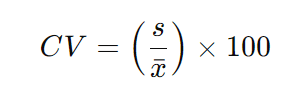
Onde:
- ( s ) é o desvio-padrão do conjunto de dados.
- x– é a média aritmética do conjunto de dados.
Essa fórmula nos dá uma medida percentual de dispersão, mostrando o quão grande é o desvio-padrão em relação à média. Quanto maior o CV, maior a variabilidade relativa do conjunto de dados.
Por que o Coeficiente de Variação é Importante?
O CV é especialmente útil em duas situações principais:
- Comparação de Conjuntos de Dados com Médias Muito Desiguais: Quando os conjuntos de dados possuem médias muito diferentes, o uso do desvio-padrão para comparar a dispersão pode ser enganoso. O CV normaliza essa diferença, proporcionando uma base justa para comparação.
- Comparação de Dados com Unidades de Medida Diferentes: O CV permite comparar a variabilidade de conjuntos de dados que utilizam diferentes unidades de medida, eliminando o impacto da unidade de medida e focando apenas na dispersão relativa.
Exemplo: calculo o que é o Coeficiente de Variação dos números 10, 11, 12, 15, 14.
Cálculo da Média Aritmética xˉ:
A média aritmética é a soma de todos os valores dividida pelo número de valores.
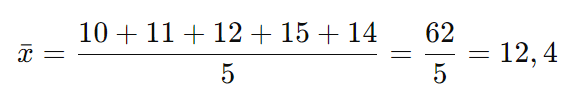
Cálculo do Desvio de Cada Valor em Relação à Média:
Subtraia a média de cada valor no conjunto de dados para encontrar o desvio de cada valor.
Desvio de 10: 10 − 12,4 = −2,4
Desvio de 11: 11 − 12,4 = −1,4
Desvio de 12: 12 − 12,4 = −0,4
Desvio de 15: 15 − 12,4 = 2,6
Desvio de 14: 14 − 12,4 = 1,6
Cálculo dos Quadrados dos Desvios:
Eleve cada desvio ao quadrado.
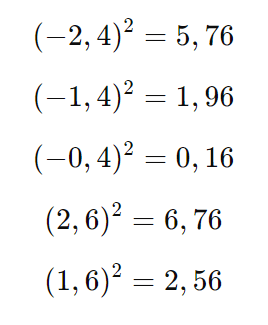
Cálculo da Variância:
A variância é a média dos quadrados dos desvios. Como estamos calculando para a população, dividimos pela quantidade total de valores n.
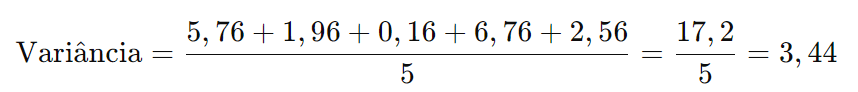
Cálculo do Desvio-Padrão s:
O desvio-padrão é a raiz quadrada da variância.
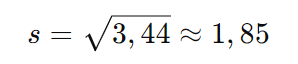
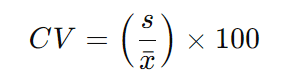
CV = 1,85 / 12,4 x 100 = 14,91%
Exemplo Prático: Analisando a Dispersão de Preços em Diferentes Mercados
Suponha que você queira comparar a dispersão dos preços de um produto em dois países. No país A, o preço médio é de $50 com um desvio-padrão de $10, enquanto no país B, o preço médio é de $70 com um desvio-padrão de $14.
- País A:
- Média: $50
- Desvio-padrão: $10
- CV = 10/50 x 100 = 20%
- País B:
- Média €70
- Desvio-padrão €14
- CV =14/70 x 100 = 20%
Novamente, embora os preços sejam em moedas diferentes, o CV igual de 20% mostra que a variabilidade dos preços em ambos os países é equivalente, permitindo uma comparação direta.
Conclusão
O coeficiente de variação é uma ferramenta indispensável para qualquer análise estatística que envolva comparação de variabilidade. Sua capacidade de normalizar dados com diferentes unidades de medida ou médias desiguais o torna um recurso valioso em diversas áreas, como economia, finanças, pesquisa de mercado e mais. Ao entender e aplicar o CV, você pode obter insights mais profundos e precisos em suas análises de dados.