A combinação é um dos conceitos mais utilizados da análise combinatória e está presente em diversas situações do dia a dia, como a formação de equipes, escolha de itens e até mesmo em jogos de loteria. Ela é aplicada quando queremos selecionar elementos de um conjunto, mas a ordem dos itens não importa. Essa característica a distingue de arranjos e permutações.
Dependendo da situação, podemos trabalhar com combinação simples ou combinação composta (também conhecida como combinação com repetição). Vamos entender cada uma delas.
📚 Quer aprofundar seus conhecimentos em Análise Combinatória e Probabilidade? Confira nossa recomendação dos melhores livros sobre o tema com exercícios resolvidos e dicas práticas. 👉Os melhores livros de Analise Combinatória e Probabilidade
O Que é Combinação?
A combinação é uma forma de calcular quantos subconjuntos podem ser formados a partir de um conjunto maior, onde não importa a disposição dos elementos, apenas quem está no grupo.
Exemplo Prático:
Imagine que você tem 4 frutas (maçã, banana, laranja, uva) e deseja escolher 2 para um lanche. Não importa se você escolhe “maçã e banana” ou “banana e maçã”, o resultado é o mesmo. Por isso, contamos apenas uma vez esse grupo.
Transforme seus estudos com o eBook Matemática Resumida: + de 90 Mapas Mentais de Matemática! Simplifique conceitos complexos, organize seus estudos e revise de forma prática e eficiente. Baixe agora e conquiste seus objetivos!
1. Combinação Simples
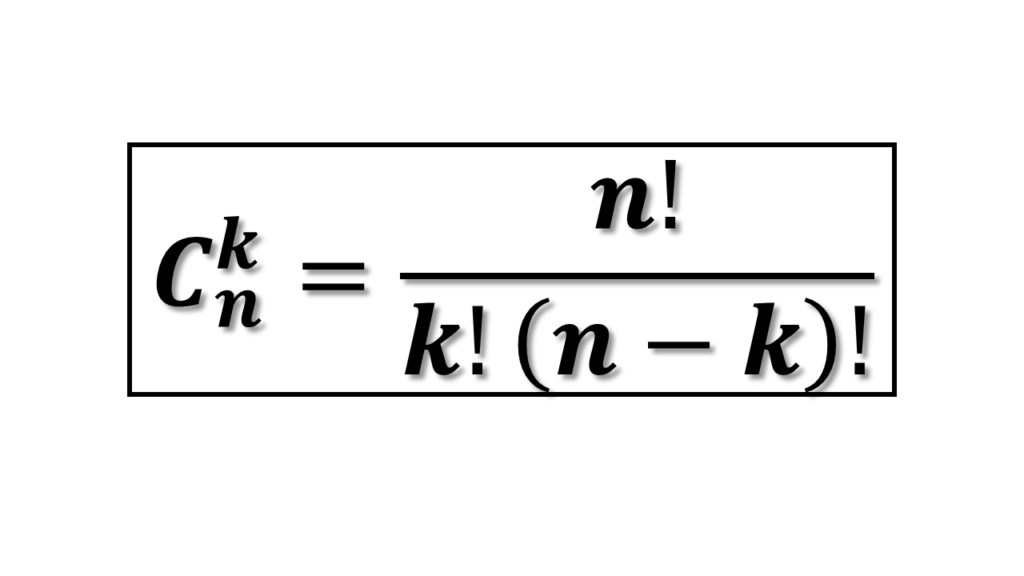
A combinação simples é usada quando selecionamos elementos de um conjunto sem permitir repetições e sem considerar a ordem.
Fórmula:
- n: número total de elementos no conjunto.
- k: número de elementos que serão selecionados.
- !: fatorial (produto de todos os números inteiros positivos até o número dado).
Exemplo Prático:
Você tem 5 colegas e quer formar uma dupla para trabalhar em um projeto. Quantas duplas diferentes podem ser feitas?
Solução:
- Total de colegas (n): 5.
- Pessoas na dupla (k): 2.
Aplicando a fórmula:
Portanto, é possível formar 10 duplas diferentes.
👉Entre no nosso canal do WhatsApp
📘 Todas as fórmulas de matemática em um só lugar! Baixe agora nosso eBook gratuito
2. Combinação Composta (ou com Repetição)
A combinação composta ocorre quando os elementos escolhidos podem se repetir. Esse tipo de combinação é usado em situações onde queremos formar grupos ou subconjuntos com repetição permitida.
Fórmula:
- n: número de elementos distintos no conjunto.
- p: número de elementos que serão selecionados, permitindo repetição.
- !: fatorial.
Exemplo Prático:
Você está escolhendo 3 bolas de sorvete em uma sorveteria que oferece 4 sabores (chocolate, morango, baunilha e limão). Quantas combinações diferentes podem ser feitas, considerando que sabores podem se repetir?
Solução:
- Total de sabores (n): 4.
- Bolas de sorvete (p): 3.
Aplicando a fórmula:
Expandindo:
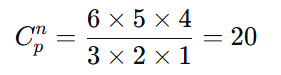
Portanto, existem 20 combinações diferentes de bolas de sorvete.
Diferença entre Combinação Simples e Composta
| Característica | Combinação Simples | Combinação Composta |
|---|---|---|
| Repetição de elementos | Não é permitida | É permitida |
| Fórmula | | |
| Exemplo Prático | Escolher 3 pessoas de um grupo de 10. | Escolher 3 bolas de sorvete com repetição. |
“Quer dominar os cálculos de possibilidades e resolver problemas de contagem com facilidade? Confira nosso artigo completo sobre as Fórmulas da Análise Combinatória e aprenda como aplicá-las no seu dia a dia com exemplos claros e objetivos!
Aplicações das Combinações
- Formação de Grupos ou Comissões:
Escolher pessoas para formar uma equipe ou um grupo de trabalho. - Escolhas com Repetição:
Selecionar itens repetíveis, como ingredientes em uma receita ou sabores em uma sobremesa. - Jogos de Loteria:
Em jogos como a Mega-Sena, a combinação simples calcula as possibilidades de escolher os números certos. - Distribuição de Recursos:
Alocar recursos repetíveis entre diferentes categorias ou pessoas.
Resumo
- Use combinação simples quando a ordem dos elementos não importa e não há repetição.
- Use combinação composta quando a ordem não importa, mas os elementos podem ser repetidos.
Quer dominar Análise Combinatória e Probabilidade de forma clara e aprofundada? Adquira já o livro Fundamentos de Matemática Elementar – Volume 5! Essa obra é referência para estudantes e concurseiros, trazendo teoria detalhada, exercícios resolvidos e aplicações práticas que vão turbinar seus estudos. Aproveite para garantir o seu e conquistar o sucesso nas provas!
Conclusão
A combinação é uma ferramenta matemática poderosa da análise combinatória assim como o arranjo e a permutação, para resolver problemas onde a ordem não é relevante. Seja na formação de equipes, escolha de itens ou cálculo de probabilidades, entender a diferença entre simples e composta permite aplicar o conceito de forma eficiente e resolver questões do cotidiano e acadêmicas.
