A congruência de triângulos é um conceito fundamental na geometria que afirma que dois triângulos são congruentes se tiverem exatamente as mesmas medidas de ângulos e lados. Isso significa que os triângulos são idênticos em forma e tamanho, embora possam estar orientados de maneira diferente ou localizados em lugares diferentes. Neste artigo, vamos explorar os principais casos de congruência de triângulos e como eles ajudam a determinar se dois triângulos são congruentes.
A geometria é uma área fundamental da matemática, dedicada ao estudo das formas, tamanhos e propriedades de figuras no plano e no espaço.
Casos de Congruência de Triângulos
A congruência de triângulos pode ser estabelecida com base em diferentes combinações de lados e ângulos. Existem quatro casos principais de congruência que são amplamente utilizados para provar a igualdade entre triângulos:
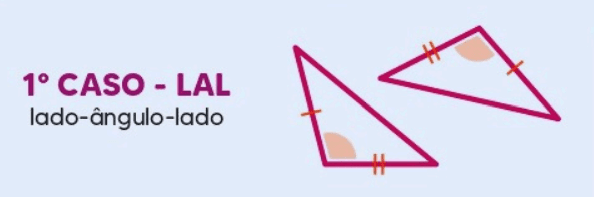
1. Caso LAL (Lado – Ângulo – Lado)
O caso LAL afirma que se dois triângulos têm dois lados e o ângulo incluído (o ângulo formado pelos dois lados) iguais, então os triângulos são congruentes. Em outras palavras, se você conhece a medida de dois lados e o ângulo entre eles, pode determinar que os triângulos são iguais.
Exemplo: Considere dois triângulos ABC e DEF onde:
- AB = DE
- AC = DF
- ∠BAC = ∠EDF
Esses triângulos são congruentes pelo caso LAL, porque dois lados e o ângulo incluído são iguais.
Propriedades:
- Os ângulos opostos aos lados iguais são iguais.
- Os lados opostos aos ângulos iguais são iguais.
2. Caso ALA (Ângulo – Lado – Ângulo)
O caso ALA afirma que se dois triângulos têm um lado e dois ângulos adjacentes iguais, então os triângulos são congruentes. Ou seja, se você conhece a medida de um lado e os ângulos ao seu redor, os triângulos são congruentes.
Exemplo: Considere dois triângulos PQR e STU onde:
- ∠PQR = ∠STU
- ∠QRP = ∠UTS
- PQ = ST
Os triângulos são congruentes pelo caso ALA porque o lado e os dois ângulos adjacentes são iguais.

Propriedades:
- Os lados opostos aos ângulos iguais são iguais.
- Os ângulos opostos aos lados iguais são iguais.
3. Caso LLL (Lado – Lado – Lado)
O caso LLL afirma que se dois triângulos têm todos os três lados correspondentes iguais, então os triângulos são congruentes. Este caso é o mais direto e rigoroso, pois envolve a igualdade de todos os lados dos triângulos.
Exemplo: Considere dois triângulos GHI e JKL onde:
- GH = JK
- HI = KL
- IG = LJ
Esses triângulos são congruentes pelo caso LLL, pois todos os lados são iguais.

Propriedades:
- Todos os ângulos internos são iguais.
- Todos os lados correspondentes são iguais.
4. Caso LAAO (Lado – Ângulo – Ângulo Oposto)
O caso LAAO (também conhecido como Lado – Ângulo – Ângulo Oposto) é uma forma um pouco mais rara de provar a congruência de triângulos. Se um lado e dois ângulos adjacentes ao lado são iguais, e o ângulo oposto ao lado conhecido é o mesmo, então os triângulos são congruentes.
Exemplo: Considere dois triângulos MNO e PQR onde:
- MN = PQ
- ∠MNO = ∠PQR
- ∠NMO = ∠QRP
- ∠M = ∠P
Os triângulos são congruentes pelo caso LAAO, pois um lado e dois ângulos são iguais, e o ângulo oposto ao lado é o mesmo.

Propriedades:
- Todos os ângulos internos são iguais.
- Todos os lados correspondentes são iguais.
Aplicações da Congruência de Triângulos
A congruência de triângulos tem várias aplicações práticas na geometria, engenharia e design. Ela é usada para:
- Provar Teoremas: Muitos teoremas geométricos, como o Teorema de Pitágoras, utilizam a congruência de triângulos para provar propriedades de figuras geométricas.
- Construção e Design: Arquitetos e engenheiros utilizam a congruência para garantir que as estruturas sejam simétricas e esteticamente agradáveis.
- Resolução de Problemas: A congruência é uma ferramenta essencial na resolução de problemas geométricos e na verificação da precisão de construções.
Resumo: Congruência de Triângulos e Seus Casos
A congruência de triângulos é um conceito fundamental na geometria que afirma que dois triângulos são congruentes se tiverem lados e ângulos correspondentes iguais. Existem quatro principais casos de congruência:
- LAL (Lado – Ângulo – Lado): Dois triângulos são congruentes se tiverem dois lados e o ângulo entre eles iguais.
- ALA (Ângulo – Lado – Ângulo): Dois triângulos são congruentes se tiverem um lado e os dois ângulos adjacentes iguais.
- LLL (Lado – Lado – Lado): Dois triângulos são congruentes se todos os três lados forem iguais.
- LAAO (Lado – Ângulo – Ângulo Oposto): Dois triângulos são congruentes se tiverem um lado e dois ângulos adjacentes iguais, e o ângulo oposto ao lado conhecido também for igual.
Esses casos são amplamente usados para provar a igualdade entre triângulos, com aplicações em teoremas geométricos, engenharia e design.

Conclusão
A congruência de triângulos é um conceito fundamental na geometria que permite comparar e analisar a igualdade entre triângulos com base em suas medidas. Conhecer os casos de congruência — LAL, ALA, LLL e LAAO — proporciona uma base sólida para resolver problemas e compreender a geometria de forma mais profunda. Ao aplicar esses casos, você pode verificar a congruência de triângulos e explorar suas propriedades com maior confiança.
Leia também
Área de Triângulos: Conceitos e Cálculos
Área de Figuras Planas: Como Calcular, Exercícios Resolvidos
Área de Circunferências: Explorando Formas e Cálculos
Explorando Ângulos: Agudo, Obtuso, Reto e Raso
Retas Paralelas e Transversais
A Soma dos Ângulos em Polígonos: Internos e Externos
Tudo Sobre Triângulos: Classificação e Propriedades
Congruência de Triângulos: Casos e Propriedades
Teorema de Pitágoras: Conceito, Provas e Aplicações
Relações Métricas no Triângulo Retângulo: Conceitos e Fórmulas Essenciais
A Lei dos Senos e a Lei dos Cossenos: Ferramentas Essenciais na Trigonometria
Quadriláteros: Área, Perímetro e Diagonais
Tudo Sobre Circunferência: Conceitos Essenciais e Cálculos
Inscrição e Circunscrição de Triângulos, Quadrados e Hexágonos Regulares
Quadriláteros Circunscritos: Teorema de Pitot
Relação Entre Retas e Circunferências: Corda, Tangente e Encontro de Tangentes












