Os conjuntos numéricos são fundamentais na estrutura da matemática e envolvem diferentes tipos de números que usamos no dia a dia e em diversas áreas científicas. Eles são classificados em grupos específicos, como números naturais, inteiros, racionais, irracionais, reais e complexos. Cada conjunto tem suas próprias propriedades e características, o que facilita a compreensão das operações matemáticas e suas aplicações.
Nesta lista de exercícios, vamos explorar esses conjuntos de maneira prática, com problemas que abrangem desde a identificação e classificação de números até a realização de operações entre eles. Além disso, cada exercício vem acompanhado de sua respectiva solução detalhada, permitindo que você revise o conceito e aprimore sua compreensão.
Prepare-se para fortalecer seus conhecimentos e dominar os conjuntos numéricos!
01 – (Enem) João decidiu contratar os serviços de uma empresa por telefone através do SAC (Serviço de Atendimento ao Consumidor). O atendente ditou para João o número de protocolo de atendimento da ligação e pediu que ele anotasse. Entretanto, João não entendeu um dos algarismos ditados pelo atendente e anotou o número 1 3 _ 9 8 2 0 7, sendo que o espaço vazio é o do algarismo que João não entendeu.
De acordo com essas informações, a posição ocupada pelo algarismo que falta no número de protocolo é a de
a) centena.
b) dezena de milhar.
c) centena de milhar.
d) milhão.
e) centena de milhão
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]

[/toggle]
02 – (Obmep) Isabel tem oito saquinhos com 3, 4, 7, 9, 11, 13, 13 e 16 balas, respectivamente. Ela distribuiu os saquinhos para três crianças, de tal modo que cada uma delas recebeu a mesma quantidade de balas. Uma das crianças recebeu o saquinho com 4 balas. Dentre os saquinhos que essa criança recebeu, qual continha mais balas?
a) O saquinho com 9 balas.
b) O saquinho com 11 balas.
c) O saquinho com 12 balas.
d) O saquinho com 13 balas.
e) O saquinho com 16 balas.
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]

[/toggle]
03 – Um número tem cinco algarismos:
__4 6 7__
Para ser divisível por 15, de quantos modos podemos preencher as casas com __ ?
a) 1 modo.
b) 3 modos.
c) 6 modos.
d) 8 modos.
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]

[/toggle]
04 – (Obmep) Um grupo de 20 amigos reuniu-se em uma pizzaria que oferece a promoção descrita na figura. Cada pizza grande foi cortada em 12 fatias e cada um dos amigos comeu 5 fatias de pizza. Quantos reais, no mínimo, o grupo pagou pelas pizzas?
a) R$ 180,00
b) R$ 210,00
c) R$ 240,00
d) R$ 270,00
e) R$ 300,00
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]

[/toggle]
05 – (Obmep) Ana Maria apertou as teclas

de sua calculadora e o resultado 2014 apareceu no visor. Em seguida, ela limpou o visor e fez aparecer novamente 2014 com uma multiplicação de dois números naturais, mas, desta vez, apertando seis teclas em vez de sete. Nesta segunda multiplicação, qual foi o maior algarismo cuja tecla ela apertou?
a) 5
b) 6
c) 7
d) 8
e) 9
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]

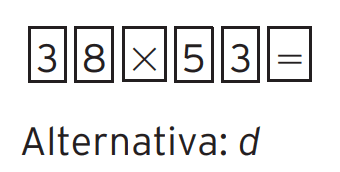
[/toggle]
06 – (Saresp) A decomposição 7 + 0,04 + 0,008 pode representar o número decimal
a) 7, 48
b) 7,408
c) 7,804
d) 7,048
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
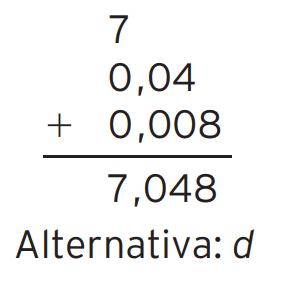
[/toggle]
07 – A fração que equivale a um numeral decimal não exato é:
a) 7/8
b) – 4/25
c) 5/6
d) 33/40
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]

[/toggle]
08 – O número 3,125 escrito na forma de fração corresponde a:

[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]

[/toggle]
09 – Escrevendo-se 3/40 na forma decimal, obtém-se:
a) 0,75
b) 0,075
c) 0,0075
d) 7,5
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
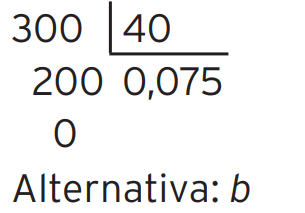
[/toggle]
10 – (Saresp) Se colocados em ordem crescente os números decimais 0,05 – 0,5 – 0,003 – 0,057 – 0,35 têm-se
a) 0,05 – 0,5 – 0,003 – 0,057 – 0,35
b) 0,003 – 0,05 – 0,057 – 0,35 – 0,5
c) 0,003 – 0,05 – 0,057 – 0,5 – 0,35
d) 0,5 – 0,35 – 0,57 – 0,05 – 0,003
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]

[/toggle]
11 – (Enem) O dono de uma oficina mecânica precisa de um pistão das partes de um motor, de 68 mm de diâmetro, para o conserto de um carro. Para conseguir um, esse dono vai até um ferro-velho e lá encontra pistões com diâmetros iguais a 68,21 mm; 68,102 mm; 68,001 mm; 68,02 mm e 68,012 mm.
Para colocar o pistão no motor que está sendo consertado, o dono da oficina terá de adquirir aquele que tenha o diâmetro mais próximo do que precisa.
Nessa condição, o dono da oficina deverá comprar o pistão de diâmetro:
a) 68,21 mm
b) 68,102 mm
c) 68,02 mm
d) 68,012 mm
e) 68,001 mm
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]

[/toggle]
12 – (Saresp) Observe a reta numérica:
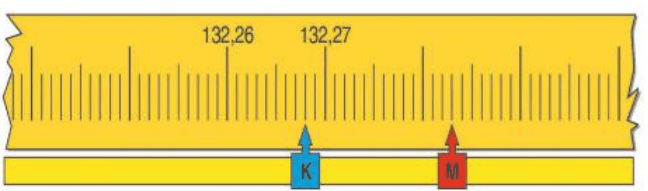
A letra K está assinalando o número 132,268. Qual é o número que a letra M está marcando?
a) 132,280
b) 132,283
c) 133,001
d) 133,300
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
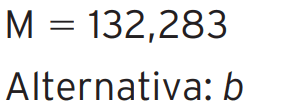
[/toggle]
13 – (Fatec-SP) Os termos da sequência
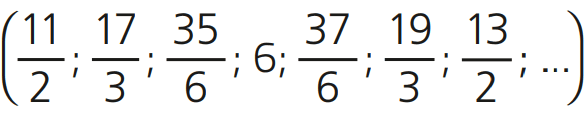
obedecem a um critério de formação. O oitavo termo dessa sequência é
a) 23/2
b) 21/2
c) 23/3
d) 22/3
e) 20/3
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]

[/toggle]
14 – A fração geratriz da dízima 0,454545… é:
a) 5/11
b) 1/20
c) 45/100
d) 454/900
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]

[/toggle]
15 – A fração geratriz da dízima 2,7333…, na sua forma irredutível, tem numerador igual a:
a) 15
b) 25
c) 41
d) 91
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]

[/toggle]
16 – Assinale a afirmação verdadeira.
a) 0,313131… é um número natural.
b) 5,47 é um número inteiro.
c) 5,171717… é um número irracional.
d) 24,656565… é um número racional.
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]

[/toggle]
17 – Assinale o número irracional, supondo que o padrão das casas decimais se repita indefinidamente.
a) 0,788888…
b) 0,7788888…
c) 0,77777…
d) 0,71727374…
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]

[/toggle]
18 – Assinale o maior entre os números seguintes:
a) 1,010101…
b) 1,0121212…
c) 1,0102102102…
d) 1,011252525…
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]

[/toggle]
19 – Multiplicando 0,3333… por 0,6 obtemos:
a) 2
b) 0,2
c) 0,02
d) 1,999
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]

[/toggle]
20 – Na reta numérica abaixo, o número irracional 0,78910111213… deve ser representado entre:

a) A e B
b) B e C
c) C e D
d) D e E
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]

[/toggle]
21 – Assinale a afirmação falsa.
a) A soma de dois números naturais quaisquer é um número natural.
b) A soma de dois números inteiros quaisquer é um número inteiro.
c) A soma de dois números racionais quaisquer é um número racional.
d) A soma de dois números irracionais quaisquer é um número irracional.
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
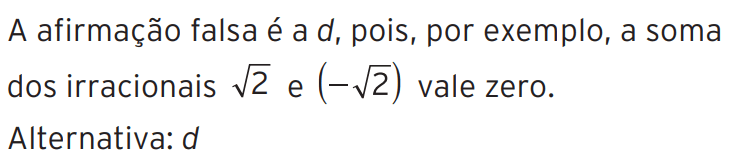
[/toggle]
21 – (Fuvest-SP) O número real x, que satisfaz 3 < x < 4, tem uma expansão decimal na qual os 999 999 primeiros dígitos à direita da vírgula são iguais a 3. Os 1 000 001 dígitos seguintes são iguais a 2 e os restantes são iguais a zero. Considere as seguintes afirmações.
I. x é irracional.
II. x > 103
III. x x 102 000 000 é um inteiro par.
Então,
a) nenhuma das três afirmações é verdadeira.
b) apenas as afirmações I e III são verdadeiras.
c) apenas a afirmação I é verdadeira.
d) apenas a afirmação II é verdadeira.
e) apenas a afirmação III é verdadeira
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]

[/toggle]













