Distância entre Retas
A distância entre duas retas no plano cartesiano pode variar dependendo de sua relação entre si. Vamos explorar as duas principais situações: retas paralelas e retas que se cruzam.
1. Retas Paralelas
Quando duas retas são paralelas, a distância entre elas é a distância perpendicular de qualquer ponto de uma das retas até a outra reta. Considerando as equações das retas na forma geral ( r1: ax + by + c1 = 0 ) e ( r2: ax + by + c2 = 0 ), a distância d entre elas é dada por:
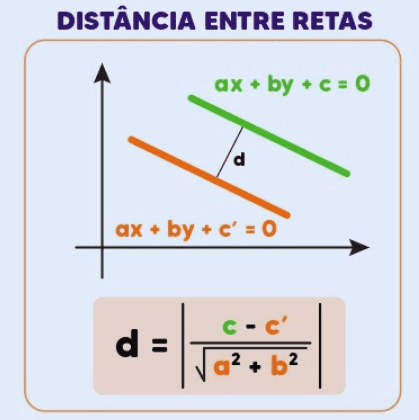
Essa fórmula calcula a menor distância entre as duas retas paralelas.
Exemplo:
Considere as retas ( r1: 2x + 3y + 5 = 0 ) e ( r2: 2x + 3y – 4 = 0 ). A distância entre elas é:
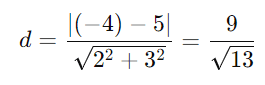
2. Retas que se Cruzam
Se as retas se cruzam, a distância entre elas é zero, pois há um ponto em comum onde as duas retas se encontram. A distância não é aplicável nesta situação.
Área de um Triângulo
A área de um triângulo pode ser calculada de diferentes maneiras, dependendo dos dados disponíveis. Aqui, exploramos dois métodos comuns: usando determinante e usando base e altura.
1. Área Usando Determinante
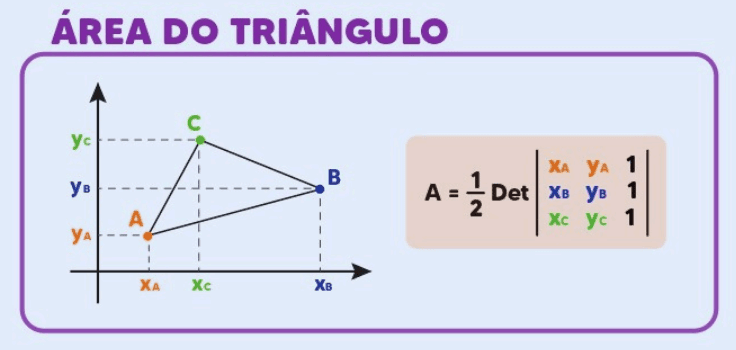
Para um triângulo cujos vértices têm coordenadas A(xA, yA), B(xB, yB) e C(xC, yC), a área pode ser calculada usando a fórmula do determinante:
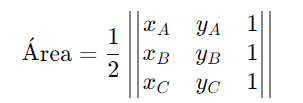
Este método é útil para calcular a área diretamente a partir das coordenadas dos vértices do triângulo.
Exemplo:
Para os pontos A(1, 2), B(3, 6), e C(5, 10), a área foi calculada como:
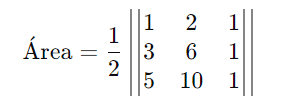
Agora, calculando o determinante:

Portanto, a área é igual a zero, o que confirma que os pontos A, B e C são colineares.
Exemplo 2: Vamos considerar três pontos A(1,2), B(4,6), e C(6,3) para calcular a área de um triângulo usando a fórmula do determinante. Esses pontos são escolhidos de forma que a área não seja zero e resulte em um número inteiro.
Substituindo os valores das coordenadas:
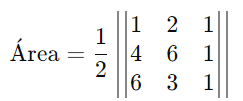

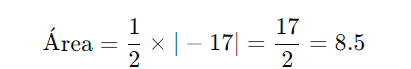
2. Área Usando Base e Altura
A fórmula mais conhecida para calcular a área de um triângulo é:
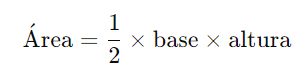
Neste método, você deve conhecer a medida da base do triângulo e a altura correspondente, que é a perpendicular traçada da base até o vértice oposto.
Exemplo:
Se um triângulo tem uma base de 6 unidades e uma altura de 4 unidades, a área é:
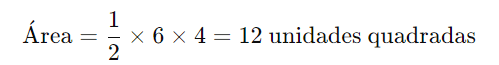
Conclusão
A compreensão da distância entre retas e da área de um triângulo são conceitos fundamentais em geometria analítica. A distância entre retas depende se as retas são paralelas ou se cruzam, e a área de um triângulo pode ser calculada de forma precisa usando determinantes ou pela fórmula tradicional de base e altura. Ambos os conceitos são amplamente aplicados em problemas geométricos e em outras áreas da matemática.
Leia também
Geometria Analítica: Pontos ⇒ Distância, Ponto Médio e Colinearidade
Distância entre Retas e Cálculo da Área de um Triângulo
Circunferência: Equação Geral e Reduzida
A Parábola: Definição, Propriedades e Equações
Elipse: Conceito, Propriedades e Equações













