A distribuição binomial é uma das mais importantes distribuições de probabilidade na estatística da matemática. Ela é usada para modelar situações em que há um número fixo de tentativas, e em cada uma delas existe uma probabilidade constante de sucesso ou fracasso. Além disso, cada tentativa deve ser independente das outras.
Definição de Distribuição Binomial
A distribuição binomial descreve o número de sucessos em uma sequência de n tentativas independentes, onde cada tentativa tem apenas dois possíveis resultados: sucesso ou fracasso. A probabilidade de sucesso em cada tentativa é representada por p, enquanto a probabilidade de fracasso é (1-p).
A função de probabilidade da distribuição binomial é dada por:
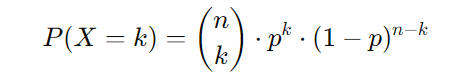
Onde:
- n é o número total de tentativas (experimentos).
- k é o número de sucessos desejados.
- p é a probabilidade de sucesso em cada tentativa.
- (1-p) é a probabilidade de fracasso em cada tentativa.
- (n k) é o coeficiente binomial, que calcula as combinações possíveis de n elementos tomados k a k.
📚 Quer aprofundar seus conhecimentos em Análise Combinatória e Probabilidade? Confira nossa recomendação dos melhores livros sobre o tema com exercícios resolvidos e dicas práticas. 👉Os melhores livros de Analise Combinatória e Probabilidade
Quando Usar a Distribuição Binomial
A distribuição binomial pode ser aplicada em qualquer cenário que atenda aos seguintes critérios:
- Número fixo de tentativas: O número de experimentos ou tentativas é definido previamente.
- Independência: As tentativas são independentes, ou seja, o resultado de uma tentativa não afeta o resultado das outras.
- Dois resultados possíveis: Cada tentativa tem apenas dois resultados possíveis: sucesso ou fracasso.
- Probabilidade constante: A probabilidade de sucesso (p) e de fracasso (1-p) é a mesma para cada tentativa.
Exemplo 1: Jogando uma Moeda
Suponha que você jogue uma moeda 5 vezes. Qual é a probabilidade de obter exatamente 3 caras?
Aqui temos:
- n = 5 (número de tentativas, ou lançamentos de moeda).
- p = 0,5 (probabilidade de sucesso, que é obter uma cara).
- k = 3 (número de sucessos, ou o número de caras que queremos).
A fórmula da distribuição binomial para esse problema é:
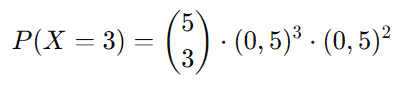
Primeiro, calculamos o coeficiente binomial:
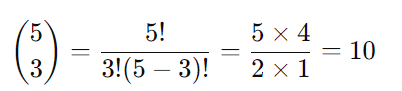
Agora, substituímos na fórmula:
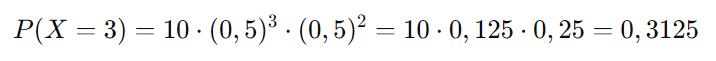
Portanto, a probabilidade de obter exatamente 3 caras ao lançar a moeda 5 vezes é 0,3125 ou 31,25%.
Transforme seus estudos com o eBook Matemática Resumida: + de 90 Mapas Mentais de Matemática! Simplifique conceitos complexos, organize seus estudos e revise de forma prática e eficiente. Baixe agora e conquiste seus objetivos!
Exemplo 2: Fabricação de Peças
Uma fábrica de peças eletrônicas sabe que 5% de suas peças produzidas são defeituosas. Se um cliente compra 20 peças, qual a probabilidade de que exatamente 2 peças sejam defeituosas?
Aqui temos:
- n = 20 (número de peças compradas).
- p = 0,05 (probabilidade de uma peça ser defeituosa).
- k = 2 (número de peças defeituosas que queremos).
A fórmula da distribuição binomial é:
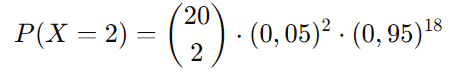
Primeiro, calculamos o coeficiente binomial:
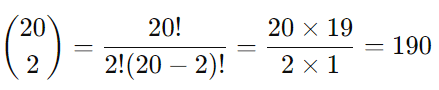
Agora, substituímos os valores na fórmula:
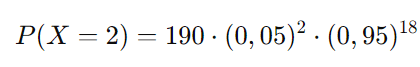
Calculando:
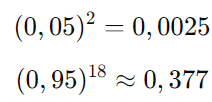
Então:
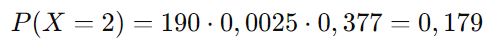
Portanto, a probabilidade de que exatamente 2 das 20 peças compradas sejam defeituosas é 0,179 ou 17,9%.
👉Entre no nosso canal do WhatsApp
📘 Todas as fórmulas de matemática em um só lugar! Baixe agora nosso eBook gratuito
Exemplo 3: Prova de Múltipla Escolha
Suponha que você faça uma prova com 10 questões de múltipla escolha, onde cada questão tem 4 alternativas e apenas uma está correta. Se você chutar todas as respostas, qual é a probabilidade de acertar exatamente 4 questões?
Aqui temos:
- n = 10 (número de questões).
- p = 0,25 (probabilidade de sucesso, que é acertar uma questão).
- k = 4 (número de acertos que queremos).
A fórmula da distribuição binomial para esse problema é:
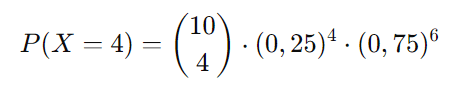
Primeiro, calculamos o coeficiente binomial:
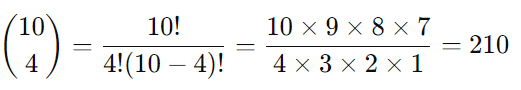
Agora, substituímos na fórmula:
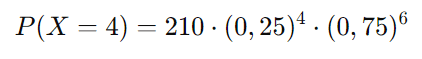
Calculando:
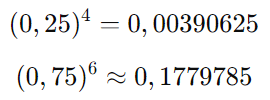
Então:
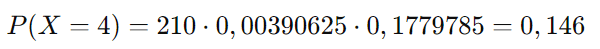
Portanto, a probabilidade de acertar exatamente 4 questões é aproximadamente 0,146 ou 14,6%.
Conclusão
A distribuição binomial é uma ferramenta poderosa na estatística, utilizada em diversas áreas como controle de qualidade, testes de hipóteses, e análise de dados. Sua aplicação depende de um número fixo de tentativas, onde cada tentativa tem dois resultados possíveis e independentes. Ao compreender e aplicar a fórmula da distribuição binomial, é possível resolver uma ampla gama de problemas práticos envolvendo probabilidade.