O Binômio de Newton é uma ferramenta poderosa na Álgebra que permite expandir potências de expressões na forma (x + a)n. Ele utiliza conceitos de análise combinatória para determinar os coeficientes dos termos no desenvolvimento, sem a necessidade de realizar multiplicações repetitivas.
Isaac Newton (1643–1727) foi um cientista, matemático, físico e astrônomo inglês, considerado uma das maiores mentes da história da ciência. Ele é conhecido por suas contribuições fundamentais à matemática, incluindo o desenvolvimento do Binômio de Newton, uma fórmula que permite expandir potências de expressões binomiais (x + a)n, aplicando conceitos de análise combinatória. Além disso, Newton é famoso por suas leis do movimento e a formulação da lei da gravitação universal, que revolucionaram a física. Sua obra-prima, Principia Mathematica, estabeleceu as bases da mecânica clássica. Newton também contribuiu significativamente à ótica e ao cálculo diferencial e integral, sendo um dos pais dessa área da matemática.
Casos Particulares e Observações Iniciais
Antes de generalizarmos, vejamos exemplos simples de expansões do binômio:
- (x + a)0 = 1
- (x + a)1 = x + a
- (x + a)2 = x2 + 2ax + a2
- (x + a)3 = x3 + 3x2a + 3xa2 + a3
Essas expansões mostram que:
- Cada termo da expansão é composto de xx e aa, com expoentes que somam nn.
- O número de termos é n + 1, e os coeficientes são simétricos.

Fórmula Geral do Binômio de Newton
Para n ∈ N, o desenvolvimento de (x + a)n é dado por:
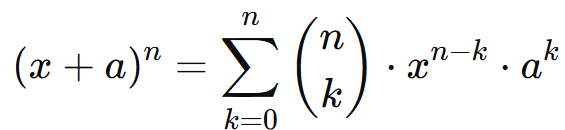
Onde:
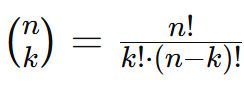
- Coeficiente binomial, que indica o número de maneiras de escolher k sucessos em n tentativas.
- xn−k: Potência decrescente de x.
- ak: Potência crescente de a.
Como Funciona na Prática?
Exemplo 1: Expansão de (x + a)3
Aplicando a fórmula:
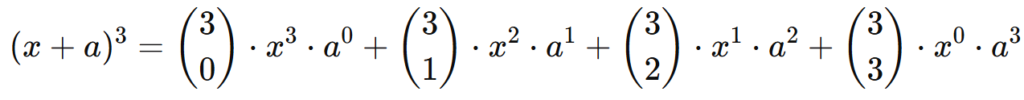
Calculando os coeficientes binomiais:
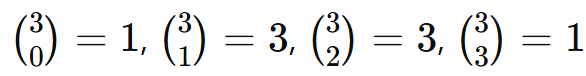
Substituindo:
(x + a)3 = 1⋅x3 + 3⋅x2a + 3⋅xa2 + 1⋅a3
(x + a)3 = x3 + 3x2a + 3xa2 + a3
Exemplo 2: Expansão de (x + 2)4
Aplicando a fórmula:
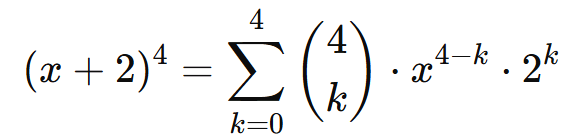
Calculando termo a termo:
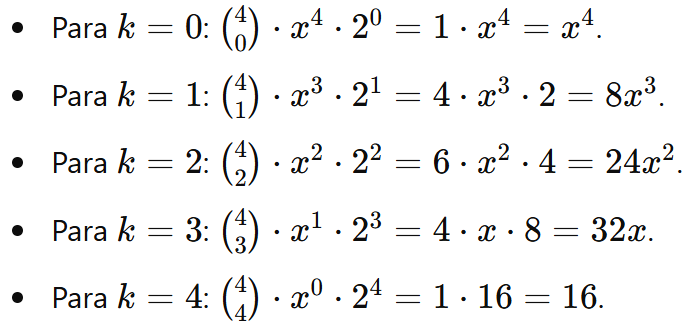
Substituindo:
(x + 2)4 = x4 + 8x3 + 24x2 + 32x + 16
Por Que o Binômio de Newton é Importante?
O Binômio de Newton é amplamente utilizado porque simplifica cálculos em diversos contextos:
- Análise Combinatória: Determina os coeficientes dos termos.
- Álgebra: Facilita a expansão de potências de polinômios.
- Probabilidade: Aplica-se em distribuições binomiais.
Curiosidade Matemática
O coeficiente binomial (nk) também aparece no Triângulo de Pascal, uma disposição triangular em que cada número é a soma dos dois números diretamente acima dele. Essa relação permite calcular coeficientes binomiais de maneira visual.
Conclusão
Aprender o Binômio de Newton é essencial na matemática, pois ele conecta conceitos fundamentais de álgebra e análise combinatória, permitindo resolver problemas de maneira eficiente e organizada. Sua aplicação vai além das expansões algébricas, sendo amplamente utilizada em áreas como probabilidade, estatística e até mesmo na física. Dominar esse conteúdo não apenas facilita a compreensão de tópicos avançados, mas também desenvolve habilidades analíticas indispensáveis para o raciocínio lógico e a resolução de problemas no estudo da matemática.