(CORREIOS – 2008 – CONSULPLAN )
Sabe-se que as expressões
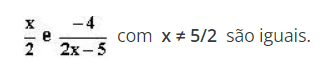
Quais são os valores reais de x que verificam essa situação?
Alternativas
A) 7
B) 0 e 7
C) Não existem valores reais de x.
D) – 1/2 e 3
E) 6 e – 1
Vamos resolver a equação que afirma que as duas expressões são iguais. Temos:

Passo 1: Eliminar os denominadores
Para eliminar os denominadores, podemos multiplicar ambos os lados da equação pelo denominador comum ((2x – 5)) de forma a simplificar. Isso nos dá:
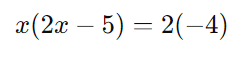
Simplificando:
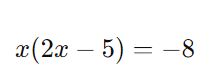
Passo 2: Expandir a equação
Agora, expandimos o lado esquerdo da equação:
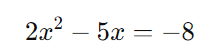
Passo 3: Reorganizar a equação
Reorganizamos a equação para colocá-la na forma padrão de uma equação quadrática:
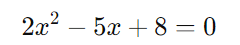
Passo 4: Aplicar a fórmula de Bhaskara
Agora, aplicamos a fórmula de Bhaskara:
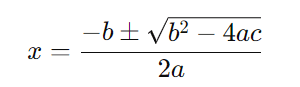
Para isso, identificamos os coeficientes:
- (a = 2)
- (b = -5)
- (c = 8)
Substituímos os valores na fórmula:
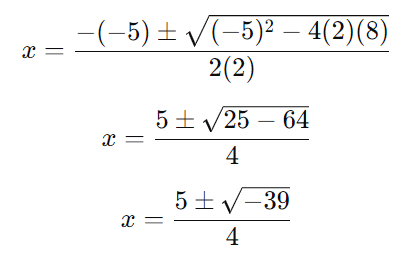
Passo 5: Analisar o discriminante
Como o discriminante (√-39) é negativo, não há soluções reais para essa equação.
Resposta:
Portanto, não existem valores reais de (x) que satisfaçam essa equação.
A resposta correta é C) Não existem valores reais de x.













