Equação do Segundo Grau: Como resolver, fórmulas, exercícios com gabarito

Ah, a Equação do Segundo Grau, aquele bicho-papão da álgebra que nos faz suar frio! Imagina só, essas belezinhas matemáticas descrevem um tipo de relação entre números que é como uma dança entre o conhecido e o desconhecido. É como se estivéssemos navegando em um rio sinuoso, onde a incógnita é uma ilha misteriosa que precisamos desvendar.

Na fórmula padrão, ax² + bx + c = 0, cada coeficiente é como uma peça de quebra-cabeça, e x é o tesouro que estamos procurando.

Quando resolvemos essa equação, estamos desvendando um enigma matemático que pode nos levar a dois destinos: raízes reais, onde encontramos terra firme, ou raízes complexas, onde navegamos em mares desconhecidos. Neste artigo, iremos nos dedicar as raízes reais e no final falaremos um pouco sobre as raízes complexas.

É como se estivéssemos desbravando um mapa antigo em busca de tesouros matemáticos escondidos. E essa habilidade de desvendar equações quadráticas? Ah, meu amigo, é como um tesouro que nos acompanha por toda a vida, permitindo-nos decifrar enigmas e desafios em todas as áreas do conhecimento.

Ah, vamos descomplicar essa história da equação do segundo grau! É tipo uma expressão matemática que se escreve assim:

A expressão matemática conhecida como equação do segundo grau é representada por: ax² + bx + c = 0. Agora, ouça o texto a seguir! A equação do segundo grau é definida por um polinômio de grau 2, ou seja, um polinômio expresso na forma ax² + bx + c, em que a, b e c são números reais.

Como identificar uma Equação do Segundo Grau

sendo ax² + bx + c = 0, temos:

• a, b e c são coeficientes, sendo a ≠ 0.
• x é a variável desconhecida.

Exemplo 1: Verifique quais das equações a seguir são do 2° grau e identifique os coeficientes a, b e c

a) 8x² + 17x + 4 = 0

Ver Solução

b) 3x – 14 = 0

Ver Solução

c) x² + x + 1 = 0

Ver Solução

d) 3 – 4x + 2x² = 0

Ver Solução

e) y² + y/20 + 4 = 0

Ver Solução

f) – x² + 3 = 0

Ver Solução

g) -7x – 2x² = 0

Ver Solução

Exemplo 2: Escreva as equações do 2° grau a seguir na forma reduzida e classifique-as em completa ou incompleta.

a) 2x² -5x = -2

Ver Solução

b) x² + 6x = 2x + 3

Ver Solução

c) y² = 8y

Ver Solução

d) -5x² = 30x + 40

Ver Solução

e) 3x(x – 2) = 2(2x − 1)

Ver Solução

f) (x + 4)(x – 5) = 5x – 16

Ver Solução

Exemplo 3: Para que valor de n a equação (5n + 2)x² – 4nx + n = 0 não é do 2° grau?

Exemplo 4: A figura ao lado representa uma caixa em forma de paralelepípedo.

a) Determine a expressão da soma das áreas das faces laterais.

Ver Solução

b) Determine a expressão da área da face destacada em vermelho.

Ver Solução

c) Se a soma das áreas das faces laterais for 880, determine a equação correspondente.

Ver Solução

Exemplo 5: Represente o número desconhecido por x e escreva a equação do 2° grau na forma reduzida que traduz cada sentença abaixo.

a) O quadrado de um número somado com o dobro desse número é igual a 99.

Ver Solução

b) O triplo do quadrado de um número menos o próprio número é igual a 30.

Ver Solução

c) Um número é igual ao quadrado desse próprio número menos 42.

Ver Solução

d) Três quintos do quadrado de um número é igual a esse número menos 40.

Ver Solução

Leia também: Equação do Primeiro Grau

Equações do Segundo Grau ou Quadráticas Incompletas

Na verdade, uma equação do segundo grau é considerada incompleta quando o coeficiente do termo quadrático (a) é diferente de zero, mas os coeficientes dos termos lineares (b) e/ou constantes (c) podem ser zero.

Por exemplo, uma equação do segundo grau ou quadrática incompleta pode ser dividida em três casos:

1° Caso: ax² = 0 (coeficiente b e c são zero)

2° Caso: ax² + bx = 0 (coeficiente c é zero)

3° Caso: ax² + c = 0 (coeficiente b é zero)

Esses são os casos possíveis de equações do segundo grau incompletas, pois o coeficiente a (do termo quadrático) é diferente de zero, enquanto b e/ou c podem ser zero.

Solução de uma Equações do Segundo Grau ou Quadrática Incompleta

1° Caso: Equação do tipo ax² = 0: Nesse caso, a solução é simples. Se a ≠ 0, então a única solução é x = 0, pois qualquer número multiplicado por zero é igual a zero.

Exemplo 1: Determine as raízes da equação quadrática 3x² = 0.

Solução: Sendo 3x² = 0, x = 0. Solução = {0}

Obs: No primeiro caso, a solução sempre será zero.

2° Caso: Equação do tipo ax² + bx = 0: Esta equação pode ser fatorada para resolver, uma vez que é possível fatorar um x comum.

A fatoração resultará em x (ax + b) = 0.

Então, as soluções são x = 0 e ax + b = 0.

Resolvendo ax +b = 0 para x, obtemos x = −a/b​.

Exemplo 1: Determine as raízes da equação quadrática 2x² + 4x = 0

Ver Solução

Exemplo 2: Determine as raízes da equação quadrática -3x² + 12x = 0

Ver Solução

3° Caso: Equação do tipo ax² + c = 0: Neste caso, podemos isolar x² dividindo ambos os lados por a, o que nos dá x² = −c/a​. Se −c/a >0, então teremos duas soluções que será -√−c/a e √−c/a.

Exemplo 1: Determine as raízes da equação quadrática -3x² + 12 = 0.

Ver Solução

Exemplo 2: Determine as raízes da equação quadrática 2x² + 36 = 0.

Ver Solução

Resolvendo Equações do Segundo Grau Completas

Para resolver as Equações Quadráticas Completas, geralmente utilizamos a Fórmula de Bhaskara porem, em casos especiais poremos resolver por Soma e Produto ou Completando Quadrado.

1° Método: Fórmula de Bhaskara

Para resolver uma equação do segundo grau do tipo

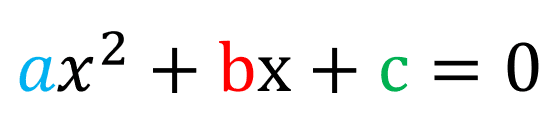
você pode usar a fórmula quadrática também conhecida como Fórmula de Bhaskara a seguir

Onde

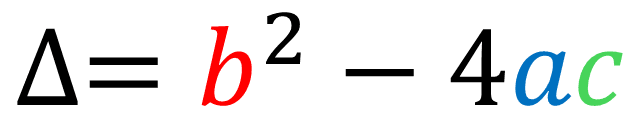
Onde

o ∆ é chamado de discriminante.

1. Se o discriminante for positivo (∆ > 0), a equação tem duas soluções reais e distintas.
2. Se o discriminante for zero (∆ = 0), a equação tem uma solução real (ou seja, as raízes são iguais).
3. Se o discriminante for negativo (∆ < 0), a equação não tem soluções reais (as raízes são números complexos).

Embora existam vários métodos para resolver equações quadráticas, a fórmula de Bhaskara é a que resolve todas elas. Dominar esta fórmula é fundamental para o sucesso na resolução de equações do segundo grau.

Exemplo 1: Determine as raízes da equação x² – 5x + 6 = 0

Ver Solução

Exemplo 2: Determine as raízes da equação 3x² – 5x – 2 = 0

Ver Solução

Resolva as equações do 2 grau abaixo utilizando Formula de Bhaskara

a) x² − 4x + 4 = 0

Ver Solução

b) x² + 8x + 16 = 0

Ver Solução

c) x² − 5x + 6 = 0

Ver Solução

d) x² + 6x + 5 = 0

Ver Solução

e) x² + 2x − 8 = 0

Ver Solução

f) x² − 4x − 5 = 0

Ver Solução

g) 4x² − 12x + 9 = 0

Ver Solução

h) 3x² + 2x − 8 = 0

Ver Solução

i) 4x² − 9x + 2 = 0

Ver Solução

j) x² − 2x + 7 = 0

Ver Solução

Questões da OBMEP, ENEM, Concurso e Vestibulares Sobre Equação do Segundo Grau

1 – OBMEP 2023 – Seja x um numero tal que x² – 3x + 1 = 0. qual é o valor de x² +1/x²

Ver Solução

👉Solução em vídeo

Outra Solução

👉Solução em vídeo

2 – (Prefeitura de Catuípe – Professor – Área: Matemática – 2024) É CORRETO afirmar que a equação (m² – 4) x² + 4x + 3 = 0 é considerada equação polinomial do 2º grau:

A)Para qualquer número inteiro m.

B)Para qualquer número racional m.

C)Para qualquer número real m, exceto quando m = 4.

D)Para qualquer número real m, exceto quando m = 2 e m = – 2.

Ver Solução

3 – (Prefeitura de Novo Hamburgo – Bibliotecário de Escola – 2024) As raízes da equação de segundo grau 2x² – 4x + 8 = 6x – 4 representam as dimensões de um retângulo. Determine o perímetro desse retângulo.

A) 3.

B) 5.

C) 6.

D)10.

E)12.

Ver Solução

Explorando o Método da Soma e Produto em Equações Quadráticas

O método da soma e produto é uma abordagem prática para encontrar as raízes de equações quadráticas do tipo x² − Sx + P, especialmente útil quando as raízes são números inteiros. Neste método, S representa a soma das raízes e P o produto delas.

Este método fundamenta-se nas seguintes relações entre as raízes:

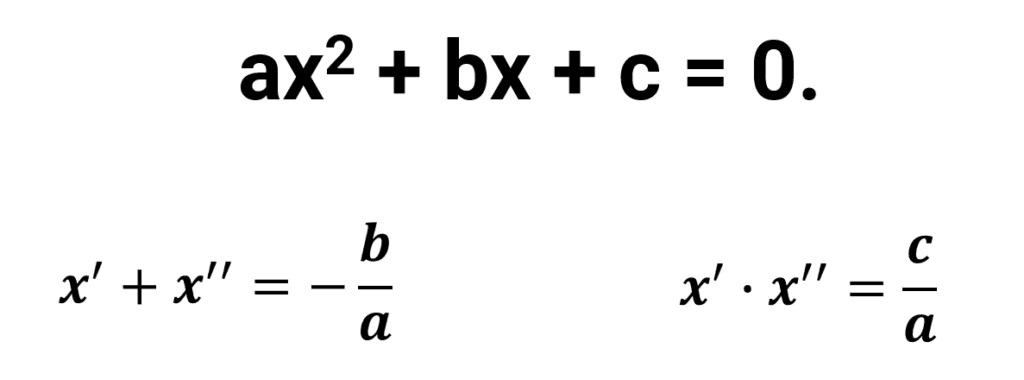
Caso o a = 1, temos que

Nesse caso, temos a expressão geral x² − Sx + P = 0, o de S é a soma das raízes e P é o produto das Raízes.

OBS: Não se prenda somente a essa forma de resolver equações do segundo grau, em casos onde as raízes não são números inteiros, fica extremamente difícil proceder por esse método.

Logo, esse métodos será útil para raízes inteiras.

Para encontrar esses números, começamos buscando dois números cujo produto seja igual a c/a. Em seguida, verificamos se esses números também satisfazem o valor da soma.

Como nem sempre as raízes de uma equação quadrática são positivas, aplicamos as regras de sinais da soma e da multiplicação para determinar quais sinais atribuir às raízes.

Para isso, temos as seguintes situações:

• (P > 0) e (S > 0) ⇒ As duas raízes são positivas.
• (P > 0) e (S < 0) ⇒ As duas raízes são negativas.
• (P < 0) e (S > 0) ⇒ As raízes têm sinais diferentes, e a de maior valor absoluto é positiva.
• (P < 0) e (S < 0) ⇒ As raízes têm sinais diferentes, e a de maior valor absoluto é negativa.

Resolva as equações do 2 grau abaixo utilizando Soma e Produto

a) x² − 4x + 4 = 0

Ver Solução

b) x² + 8x + 16 = 0

Ver Solução

c) x² − 5x + 6 = 0

Ver Solução

d) x² + 6x + 5 = 0

Ver Solução

e) x² + 2x − 8 = 0

Ver Solução

f) x² − 4x − 5 = 0

Ver Solução

g) 4x² − 12x + 9 = 0

Ver Solução

O método da soma e do produto para a ≠ 0

Seja a equação do segundo grau abaixo

O primeiro passo é multiplicar o coeficiente a pelo coeficiente c, gerando assim uma noca equação:

Depois utilize o método  – Solteiro (ST) Pega Muito (PM)

• ST – SOMA TROCA O SINAL
• PM – PRODUTO MANTÊM O SINAL

Agora precisamos encontrar dois números x¹ e x² onde a sua soma da -3 e o seu produto da -18

Desse modo, a solução do problema proposto é 1 e -2.

h) 3x² + 2x − 8 = 0

Ver Solução

i) 4x² – 8x – 12 = 0

Ver Solução

Equações Quadráticas: Exercícios sobre Soma e Produto

Exercício 1 (Prefeitura de Vacaria – RS – Técnico em Enfermagem 2021)

A soma e o produto das raízes da equação do segundo grau 2x² + 4x – 6 = 0 são, respectivamente: Alternativas

A) -2 e -3.

B) -3 e -2.

C) 2 e 3. 

D) 3 e 2.

E) 2 e -6. 

Ver Solução

Exercício 2: A equação x² – x – 30 = 0 apresenta duas raízes iguais a:

a) – 6 e – 5
b) – 1 e – 30
c) 6 e – 5
d) 30 e 1
e) – 6 e 5

Ver Solução

Exercício 3: Determine as raízes da equação x² − 8x + 12 = 0

Ver Solução

Fatorando uma Equação do Segundo Grau

Para fatora uma equação do segundo grau ou trinômio do segundo grau podemos utilizar a relação:

Se ax² + bx + c = 0 é uma equação do segundo grau e e x₁ e x₂ são raízes dessa equação, então

ax² + bx + c = a(x – x₁)(x – x₂)

Resolvendo equações do 2° grau pelo método de completar quadrados

O método de completar quadrados é uma técnica valiosa que podemos empregar na resolução de equações do segundo grau. Embora nem sempre seja a abordagem mais eficaz para esses problemas específicos, compreender este método pode ser fundamental para o desenvolvimento de habilidades matemáticas essenciais. Ele se assemelha às técnicas de produtos notáveis, por isso é crucial estudar este tópico para compreender plenamente o método, também conhecido como quadrado perfeito.

Quando uma equação do segundo grau é expressa na forma de produto notável, isso pode simplificar significativamente o processo de cálculo para encontrar suas raízes. Frequentemente, as raízes são obtidas simplesmente ao reescrever a equação dessa maneira.

Sabemos desde o ensino fundamental que :

(a + b)² = a² + 2ab + b²

(a – b)² = a² – 2ab + b²

Estamos acostumados a sempre observar essas igualdades da esquerda para a direita, sem perceber o quão útil pode ser para resolver uma equação quadrática, olhar da direita para a esquerda.

Vamos estabelecer um passo a passo para esse método

1° Passo: Representação do quadrado perfeito

Baseado na interpretação geométrica dada pelos gregos, considerando a expressão (a + b)², o matemático co-árabe Al-khowarizmi no século IX, estabeleceu um processo geométrico para a resolução de equações de 2° grau com uma incógnita.

Inicialmente, observe a Figura 1 que representa geometricamente a expressão (a+b)²:

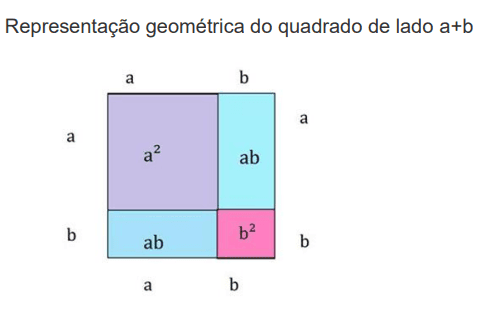
Note que (a + b)² = a² + 2ab + b², onde a² é a área do quadrado de lado a, ab é a área de cada um dos retângulos de lados a e b respectivamente, e a área do
quadrado de lado b é b².

2° Passo: Completando o quadrado

Baseando-se na interpretação geométrica conforme a Figura acima, considere a expressão: x² + 6x

Note que ela pode ser reescrita como x² + 2(3x). Observe que x² é a área de um quadrado cujo lado mede x, e 3x é a área do retângulo de lados 3 e x, respectivamente. A Figura abaixo ilustra essa expressão de forma geométrica.

Qual valor devemos acrescentar a x²+ 2.(3x) para que a expressão represente um quadrado perfeito? Para responder essa pergunta, observe a Figura abaixo.

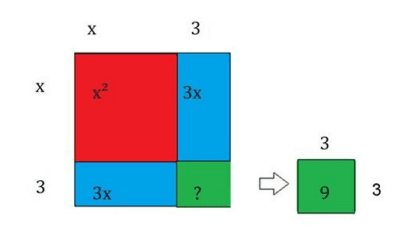
Portanto, devemos adicionar o número 9 para que a expressão x²+ 2(3x) se torne um quadrado perfeito. Assim:

x² + 6x = x² + 6x + 9 – 9 = (x+3)² – 9

3° Passo: Resolvendo equações quando o quadrado não é perfeito

Para resolver a equação x²+6x+8=0 utilizando o completamento de quadrado, vamos considerar primeiramente a expressão x² + 6x. Assim, teremos:

x² + 6x= x² + 2(3x).

Note que o quadrado será igual a segunda figura, pois x² é a área de um quadrado de lado x, e 3x é área do retângulo de lados 3 e x.

Porém, a equação dada é x²+6x+8=0 e subtraindo 8 em ambos os lados da igualdade temos:

x² + 6x + 8 – 8 = -8

x² + 6x = -8

Para completar o quadrado é necessário adicionar 9 em ambos os lados da igualdade:

x² + 6x + 9 = -8 + 9

x² + 6x + 9 = 1

Fatorando o trinômio do quadrado perfeito no 1° membro, temos:

(x + 3)² = 1

As expressões que satisfazem a equação anterior são:

(x+3) = ±√1

(x+3) = √1 ⇒ x+3 = 1 ⇒ x = 1 – 3 ⇒ x = – 2

(x+3) = -√1 ⇒ x+3 = -1 ⇒ x = -1 – 3 ⇒ x = -4

Solução S = {- 4, – 2}

4° passo: Quando o fator que contém x não é múltiplo de 2

Considere a expressão x² + 7x. Podemos reescrever essa expressão de forma conveniente:

x²+7x= x² + 2(7/2)x

Note que x² é a área de um quadrado no qual os lados medem x e (7/2)x é a área do retângulo tal que um dos lados mede x e o outro (7/2). Observe a Figura abaixo.

Para completar o quadrado ilustrado na Figura acima é preciso acrescentar um quadrado de lados (7/2) ou seja, um quadrado de área (7/2)² então:

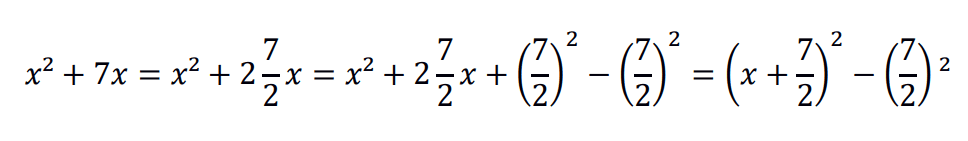
Exercício 1: Resolver a equação

x² + 2x − 3 = 0

Passando o -3 para o segundo membro temos

x² + 2x = 3

Colocaremos o primeiro membro da expressão acima da forma a² + 2ab + b² nesse caso, a = x, e nos resta encontrar o valor de b. Veja que 2x = 2ab, sendo x = a, b = 1.

Ligo temos,

(x + 1)² – 1² = 3 ⇒ (x + 1)² – 1= 3 ⇒ (x + 1)² = 3 + 1 ⇒ (x + 1)² = 4 ⇒ (x + 1) = ± √4 ⇒ x + 1= ± 2

Agora iremos calcular o x’ e o x”

x’ = -1 + 2 = 1

x” = -1 – 2 = -3

Logo solução {-3, 1}

Apesar de representarem a mesma igualdade, esta última parece visualmente mais fácil de resolver. O método que utilizamos é conhecido como completar o quadrado em uma equação quadrática. Vamos generalizar o método:

x² + bx + c = 0

Queremos que o termo “bx” seja duas vezes o primeiro termo vezes o segundo, para transformá-lo em um quadrado. Portanto, tomamos como o primeiro termo “x”. O segundo termo será “b/2”. Com isso, tomamos o quadrado deste termo e somamos à fórmula, e também tomamos sua diferença. Assim, a expressão fica

x² + bx + (b/2)² – (b/2)² + c = 0

Assim podemos simplificar como:

x² + bx + (b/2)² = + (b/2)² – c

x² + bx + (b/2)² = b²/4 – c

x² + bx + (b/2)² = (b²– 4c)/4

(x + b/2)² = (b²– 4c)/4

Para o caso em que (b²– 4c)/4 > 0 a equação terá duas raízes reais

Para o caso em que (b²– 4c)/4 = 0 a equação terá duas raízes reais e opostas

Para o caso em que (b²– 4c)/4 < 0 a equação não terá raízes reais

Resolva as equações do 2 grau abaixo pelo método de completar quadrados

a) x² − 4x + 4 = 0

b) x² + 8x + 16 = 0

c) x² − 5x + 6 = 0

d) x² + 6x + 5 = 0

e) x² + 2x − 8 = 0

f) x² − 4x − 5 = 0

g) 4x² − 12x + 9 = 0

h) 3x² + 2x − 8 = 0

i) 4x² − 9x + 2 = 0

Demonstração da Fórmula de Bhaskara

Seja ax² + bx + c = 0, temos que

ax² + bx = – c (multiplicando por 4a ambos os membros temos):

4a²x² + 4abx = – 4ac (somando b² a ambos os membros temos):

4a²x² + 4abx + b² = – 4ac + b² (Note que o primeiro membro é um produto notável (2ab + b)², Logo

(2ax + b)² = b² – 4ac (tirando a raiz quadrada temos:

2ax + b = ±√(b² – 4ac)

x = [- b ±√(b² – 4ac)]/2a

Nesse caso, está demonstrada o Fórmula de Bhaskara

Equação Biquadrada

Uma equação biquadrada é uma equação polinomial de quarto grau, que pode ser escrita na forma:

ax⁴ + bx² + c = 0

Para resolver uma equação biquadrada, você pode seguir os seguintes passos:

Substituição: Faça uma substituição para transformar a equação biquadrada em uma equação quadrática, utilizando uma variável conveniente. Por exemplo, substitua y = x² para obter uma equação quadrática em y.

Resolva a equação quadrática resultante: Após a substituição, você terá uma equação quadrática em uma nova variável (no exemplo acima, y). Resolva essa equação quadrática usando métodos como fatoração, completando o quadrado ou a fórmula de Bhaskara.

Encontre os valores de x: Depois de encontrar os valores de y, substitua de volta na equação original para encontrar os valores de x.

Verifique as soluções: Verifique se todas as soluções obtidas satisfazem a equação original.

Lembre-se de que, como uma equação biquadrada é do quarto grau, ela pode ter até quatro soluções reais ou complexas, dependendo dos coeficientes da equação.

y⁴ – 10y² + 9 = 0 → equação biquadrada

(y²)² – 10y² + 9 = 0 → também pode ser escrita assim.

Substituindo variáveis: y² = x, isso significa que onde for y² iremos colocar x.

x2 – 10x + 9 = 0 → agora resolvemos essa equação do 2º grau encontrando x` e x“

a = 1    b = -10     c = 9

∆ = b2 – 4ac
∆ = (-10)2 – 4 . 1 . 9
∆ = 100 – 36
∆ = 64

x = (-b ±√∆ )/2a

x = (- (- 10) ±√64 )/2.1

x = (10 ± 8 )/6 (nesse momento vamos dividir o calculo em duas partes, proveniente do ±)

x₁ = (10 + 8)/2 = 18/2 = 9

x₂ = (10 – 8)/2 = 2/2 = 1

Essas são as raízes da equação x² – 10x + 9 = 0, para encontrarmos as raízes da equação biquadrada y⁴ – 10y² + 9 = 0 devemos substituir os valores de x’ e x” em y² = x.

Para x = 9
y2 = x
y2 = 9
y = ± √9
y = ± 3

Para x = 1
y2 = x
y2 = 1
y = ± √1
y = ±1

Portanto, a solução da equação biquadrada será:

S = {-3, -1, 1, 3}.

Problemas de equações do segundo grau

1 – Cláudio decidiu construir um depósito retangular. Para facilitar e economizar, optou por aproveitar uma parede existente. Com os tijolos de que dispunha, podia erguer uma parede de 16 metros de comprimento e com altura suficiente para seu depósito, que deveria ter 30 m² de área. Quais as possíveis dimensões do depósito?

Resposta: 3m × 10m ou 5m × 6m

2 – Num retângulo, cuja área é 65 m², a base é 3 metros menor que o dobro de sua altura. Obtenha sua base.

Resposta: 10m

3 – Na equação x² + (k + 2)·x + k + 10 = 0, a soma das raízes é igual ao produto delas. Obtenha essas raízes.

Resposta: 2 e 2

4 – Comprei algumas garrafas de um bom vinho por 540 reais. Por ter obtido um desconto de 15 reais no preço de cada garrafa, consegui comprar 3 garrafas a mais do que previra originalmente. Quantas garrafas de vinho comprei?

Resposta: 12 garrafas

5 – Ao acordar, Bárbara viu que sua mãe lhe deixou um bilhete dizendo para ir ao mercado comprar ovos e refrigerantes. Ela olhou o bilhete e verificou que o resultado da soma do número de ovos com o número de refrigerantes que deveria comprar era 10. Saindo de casa, sua irmã Marcela lhe disse: “Bárbara,
não esqueça que o produto do número de ovos com o número de refrigerantes que você deve comprar é 21! Além disso, não esqueça que você deve comprar mais ovos do que refrigerantes!”. Bárbara agradeceu à sua irmã pelo aviso e voltou para casa com a quantidade certa de ovos e refrigerantes. Quantos ovos e quantos refrigerantes Bárbara comprou?

Resposta: 7 ovos e 3 refrigerantes

6 – Isaias comprou um terreno de forma quadrada com lado medindo 2x metros. Após muito trabalho, decidiu ampliar sua casa e adquiriu um terreno vizinho, de forma retangular, com 10 metros de frente e 2x metros de comprimento. No ano seguinte, quando recebeu seu o carnê do IPTU, nele constava
que a área total do terreno (anterior mais o novo) media 416 m². Qual as dimensões de cada terreno?

Resposta: Terreno 1: 16m × 16m. Terreno 2: 16m × 10m

7 – (FUVEST). A equação do segundo grau ax² − 4x − 16 = 0 tem uma raiz cujo valor é 4. A outra raiz é:
(a) 1

(b) 2

(c) 3

(d) −1

(e) −2

Resposta: (E)

8 – Uma bola é largado do alto de um edifício e cai em direção ao solo. Sua altura h em relação ao solo, t segundos após o lançamento, é dada pela expressão h = −25t² + 625. Após quantos segundos do lançamento a bola atingirá o solo?
(a) 2, 5

(b) 5

(c) 7

(d) 10

(e) 25

Resposta: (B)

9 – (ETF – RJ). A equação x² − (2m − 1)x + m(m − 1) = 0 admite raízes reais para:
(a) m = 0

(b) m = 2

(c) m = 3

(d) qualquer valor de m

(e) (2m − 1)2 + 4m(m − 1) = 0

Resposta: (D)

10 – (FUVEST). Para que valores de a a equação ax² + ax + a = 0 tem duas raízes reais distintas?

(a) somente para a = 0

(b) para todo a > 0

(c) para todo a < 0

(d) para todo a real

(e) para nenhum a real

Resposta: (E)

11 – A soma de todas as raízes de (2x² + 4x − 30) · (3x − 1) = 0 é:
(a) −5/3
(b) 5/3
(c) −3/5
(d) 3/5
(e) 0

Resposta: (A)

12 – (UNIFOR). Um grupo de amigos comprou um presente por R$ 6 300,00. Pretendiam dividir essa quantia entre si, em partes iguais. Como 2 membros do grupo não puderam cumprir o compromisso, cada um dos restantes teve sua parcela aumentada de R$ 360,00. O número de pessoas do grupo era, inicialmente:
(a) 11

(b) 10

(c) 9

(d) 8

(e) 7

Resposta: (E)

13 – (FUVEST). Sejam x₁ e x₂ as raízes da equação 10x² + 33x − 7 = 0. O número inteiro mais próximo do número 5x₁x₂ + 2(x₁ + x₂) é:
(a) −33

(b) −10

(c) −7

(d) 10

(e) 33

Resposta: (B)

14 – (UFMG) Considere a equação (x² − 14x + 38)² = 112. Qual é o número de raízes distintas dessa equação?

Resposta: 3 raízes distintas

15 – (FUVEST) Para a fabricação de bicicletas, uma empresa comprou unidades do produto A, pagando R$ 96,00, e unidades do produto B, pagando R$ 84,00. Sabendo-se que o total de unidades compradas foi de 26 e que o preço unitário do produto A excede em R$ 2,00 o preço unitário do produto B, determine o número de unidades de A que foi comprado.

Resposta: 12 unidades

16 – (CESPE – 03/02/2019 – SEFAZ-RS – Auditor Fiscal da Receita Estadual) A soma das soluções reais da equação (2x² – 20x) / (x² – 6x) = 2x, em que x ≠ 0 , é igual a

A) 7.

B) 2.

C) 5.

D) 7.

E) 10.

17 – (CESPE SEBRAE-AC) Julgue o item seguinte. As raízes da equação x² – 4x + 2 = 0 são números racionais.
( )CORRETO

( x )ERRADO

18 – (CESPE-2015) Considerando a função f(x) = x² – 2x – 35, definida para todos os números reais, julgue o item seguinte As raízes da equação f(x) = 0 são todas positivas.
( )CERTO

( )ERRADO

19 – (PM-ES-2008-CEBRASPE) Considere que as cadeias de um município mantenham 160 albergados igualmente distribuídos em cada uma das celas e que, com a reforma de 20 dessas celas, para manter todos os albergados, tenha sido necessário redistribuir para cada uma das celas restantes 4 albergados. Nessa situação, é correto afirmar que a quantidade total de celas nas cadeias desse município é superior a 45 e que, em cada cela, inicialmente, havia menos de 3 albergados.
( )CERTO

( )ERRADO

20 – (CESPE – 2016 – CPRM – Técnico em Geociências – Hidrologia) Considerando-se os 365 dias de um ano, numerados sequencialmente de 1 a 365, a função y = – 0,1x² +40x, em que x = 1, 2, …, 365, estima-se a quantidade de litros de água desperdiçados no dia x em vazamentos na rede de distribuição de determinada cidade. Nesse caso, o desperdício equivalente a 3m³ ocorreu em um dia do mês de

A) janeiro e um dia do mês de dezembro.

B) janeiro e em um dia do mês de julho.

C) fevereiro e em um dia do mês de setembro.

D) abril e em um dia do mês de novembro.

21 – (ESCRITURÁRIO-BANCO DO BRASCILCESPE/CEBRASPE) Um grupo de amigos saiu para assistir a um filme no cinema do bairro. Lá chegando, constataram que o preço das entradas para todos, refrigerantes e pipoca era de R$ 585,00. Esse valor deveria ser dividido inicialmente entre todos do grupo, mas, por delicadeza, os integrantes do grupo que moravam nesse bairro revolveram dividir entre eles o valor correspondente ao que cabia aos 4 integrantes que não moravam no bairro, o que acrescentou à despesa de cada um dos primeiros a quantia de R$ 20,00. Com base nessa situação hipotética, julgue os itens que se seguem.
No grupo de amigos havia menos de 8 moradores do bairro onde fica o cinema e a cada um deles coube uma despesa superior a R$ 70,00.

( )CORRETO

(x )ERRADO

22 – (UNICAMP) As soluções da equação: 3(x² − 5x + 6) = x² − 4x + 9 são iguais a

A) 1 e 4,5.

B) 1 e 2.

C) 2 e 9. 

D) 4,5 e 9. 

23 – (VUNESP – 2018) A soma das raízes da equação x² – (3a – 2b)x + 2b – 6a = 0 é igual a 8 e seu produto é igual a –20. Desse modo, o resultado da operação a^b : b^a é igual a

A) 2

B)-1

C)4

D)1/2

E) 1

Lista de exercício Equação do Segundo grau em pdf

1 – Lista de exercício Equação do 2° grau em pdf

2 – Lista de exercício Equação do 2° grau em pdf

3 – Lista de exercício Equação do 2° grau em pdf

4 – Lista de exercício Equação do 2° grau em pdf

5 – Lista de exercício Equação do 2° grau em pdf

6 – Lista de exercício Equação do 2° grau em pdf

Mapa Mental Equação do Segundo Grau

Um mapa mental sobre a equação do segundo grau pode ser organizado de várias maneiras, mas aqui está uma estrutura básica de forma eficiente.

Baixe Mapa Mental Equação do 2° Grau em PDF