Introdução
Estatística é a área da matemática que lida com a coleta, análise e interpretação de dados. Ela é usada em diversas áreas para entender informações e tomar decisões. Neste artigo, vamos explorar conceitos básicos de estatística, como média, moda, mediana, variância e desvio padrão, com exemplos simples para facilitar o entendimento.
Média
A média aritmética é um valor que representa a soma de todos os números de um conjunto, dividida pelo total de números. Ela é usada para encontrar um valor “típico” do conjunto.
Fórmula:
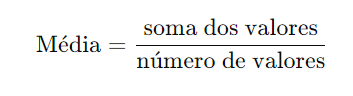
Exemplo 1:
Considere os números: 4, 8, 15, 16, 23.
Passo 1: Some todos os números:
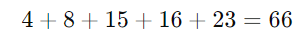
Passo 2: Divida pelo número de valores:
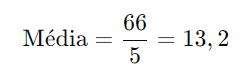
Exemplo 2:
Considere os números: 10, 20, 30, 40, 50.
Passo 1: Some todos os números:
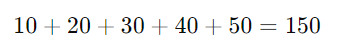
Passo 2: Divida pelo número de valores:
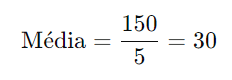
Moda
A moda é o número que aparece com mais frequência em um conjunto de dados. Em alguns conjuntos, pode haver mais de uma moda ou nenhuma.
Exemplo 1:
Considere os números: 2, 4, 4, 6, 8.
O número 4 aparece mais vezes, então a moda é 4.
Exemplo 2:
Considere os números: 1, 2, 2, 3, 3, 4.
Os números 2 e 3 aparecem mais vezes, então este conjunto tem duas modas: 2 e 3.
Mediana
A mediana é o número que fica no meio de um conjunto de dados quando os números estão em ordem crescente. Se o número de valores for par, a mediana é a média dos dois números do meio.
Exemplo 1:
Considere os números: 7, 9, 12, 15, 18.
Como há cinco números, o terceiro valor (12) é a mediana.
Exemplo 2:
Considere os números: 5, 7, 9, 11, 13, 15.
Como há seis números, a mediana é a média dos dois valores centrais:
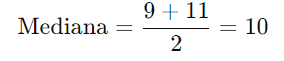
Variância
A variância mede o quão espalhados os números de um conjunto estão em relação à média. Quanto maior a variância, mais espalhados os números estão.
Fórmula:
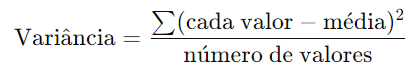
Exemplo 1:
Considere os números: 2, 4, 4, 6, 8.
Passo 1: Calcule a média:
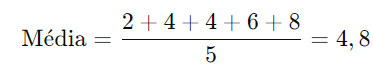
Passo 2: Subtraia a média de cada valor e eleve ao quadrado:
(2 – 4,8)2 = 7,84,
(4 – 4,8)2 = 0,64,
(4 – 4,8)2 = 0,64,
(6 – 4,8)2 = 1,44,
(8 – 4,8)2 = 10,24
Passo 3: Some esses valores e divida pelo número de valores:
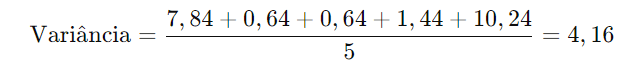
Exemplo 2:
Considere os números: 3, 7, 7, 19, 21.
Passo 1: Calcule a média:
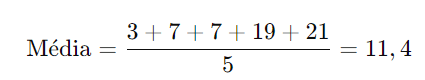
Passo 2: Subtraia a média de cada valor e eleve ao quadrado:
(3 – 11,4)2 = 70,56,
(7 – 11,4)2 = 19,36,
(7 – 11,4)2 = 19,36,
(19 – 11,4)2 = 57,76,
(21 – 11,4)2 = 92,16
Passo 3: Some esses valores e divida pelo número de valores:
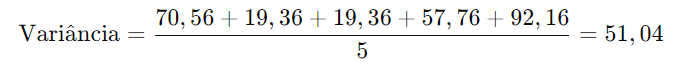
Desvio Padrão
O desvio padrão é a raiz quadrada da variância e mostra o quanto, em média, os valores se desviam da média. Ele é muito usado para medir a dispersão dos dados.
Fórmula:
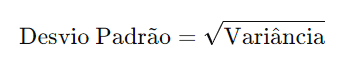
Exemplo 1:
Considerando o exemplo da variância anterior:

Exemplo 2:
Considerando o exemplo da variância anterior:
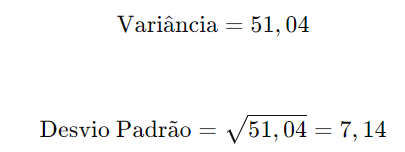
Conclusão
A estatística nos ajuda a entender e interpretar dados de forma clara. Conceitos como média, moda, mediana, variância e desvio padrão são fundamentais para analisar dados no dia a dia. Os exemplos resolvidos mostram como aplicar esses conceitos de maneira simples e prática.
Lista de exercícios Estatística
1 – Considere o conjunto de números: 10, 15, 20, 25, 30. Qual é a média aritmética desse conjunto?
a) 20
b) 22
c) 25
d) 24
e) 18
2 – Qual é a moda do seguinte conjunto de dados: 7, 12, 15, 12, 18, 7, 12?
a) 7
b) 12
c) 15
d) 18
e) Não há moda
3 – Dado o conjunto de valores: 5, 9, 12, 15, 20, 22, 25, qual é a mediana?
a) 12
b) 15
c) 16,5
d) 20
e) 13,5
4 – Considere o conjunto de números: 2, 4, 6, 8, 10. Qual é a variância?
a) 2
b) 5
c) 8
d) 10
e) 12
5 – Com base no conjunto de números: 3, 6, 9, 12, 15, calcule o desvio padrão.
a) 3,74
b) 4,32
c) 4,89
d) 5,14
e) 5,48
6 – Em uma pesquisa, os salários de 10 trabalhadores em uma empresa foram registrados como: R$ 1500, R$ 1800, R$ 2000, R$ 1800, R$ 2200, R$ 1500, R$ 1800, R$ 1800, R$ 2000, R$ 2200. Qual é a moda dos salários?
a) R$ 1500
b) R$ 1800
c) R$ 2000
d) R$ 2200
e) Não há moda
7 – Considere os números: 100, 200, 300, 400, 500. Qual é a diferença entre a média e a mediana?
a) 0
b) 50
c) 100
d) 150
e) 200
8 – Se a variância de um conjunto de dados é 36, qual é o desvio padrão?
a) 4
b) 6
c) 8
d) 9
e) 12
9 – Um aluno fez 5 provas com as seguintes notas: 7,5; 8,0; 6,5; 9,0; 7,0. Qual é a média das notas do aluno?
a) 7,0
b) 7,2
c) 7,6
d) 8,0
e) 8,2
10 – Dado o conjunto de valores: 13, 17, 21, 29, 34, 38, 42, 47, qual é a mediana?
a) 29
b) 31,5
c) 34
d) 36
e) 38
Gabarito
Exercício 1: a) 20
Exercício 2: b) 12
Exercício 3: b) 15
Exercício 4: b) 5
Exercício 5: a) 3,74
Exercício 6: b) R$ 1800
Exercício 7: a) 0
Exercício 8: b) 6
Exercício 9: c) 7,6
Exercício 10: b) 31,5













