A estatística é a ciência que transforma números em informações. Ela desempenha um papel fundamental em diversas áreas do conhecimento, auxiliando na tomada de decisões baseadas em dados concretos. Por meio de métodos que envolvem coleta, organização, análise e interpretação de dados, a estatística fornece as ferramentas necessárias para compreender fenômenos complexos e identificar padrões.

Por que Estudar Estatística?
No mundo atual, onde dados são gerados a todo momento, compreender estatística é mais importante do que nunca. Desde prever tendências econômicas até medir o impacto de políticas públicas, a estatística ajuda a responder perguntas fundamentais, como:
- Qual é o perfil dos clientes de uma empresa?
- Como as notas de uma turma variam em relação à média?
- Qual a probabilidade de um evento ocorrer?
Estatística Descritiva: O Primeiro Passo
A estatística descritiva é uma das principais ramificações dessa ciência. Ela se concentra na organização e apresentação de dados por meio de tabelas, gráficos e cálculos de medidas estatísticas, como média, mediana e desvio padrão. Essas ferramentas simplificam a interpretação dos dados, permitindo que conclusões sejam extraídas de forma rápida e clara.
Exemplo:
Considere uma pesquisa sobre as idades de 30 participantes de um evento. A estatística descritiva permite organizar esses dados em intervalos de idade, criar gráficos ilustrativos e calcular a média para obter um panorama geral.
Com isso, a estatística não apenas organiza o caos dos números, mas também revela informações valiosas, essenciais para a compreensão de qualquer conjunto de dados.
Conceitos Fundamentais da Estatística
População
A população é o conjunto total de elementos que compartilham características em comum e que são o foco de um estudo. Pode incluir pessoas, objetos ou eventos.
Exemplo: A altura de todos os jovens de uma cidade interessados em participar de um programa esportivo.
Amostra
Uma amostra é um subconjunto da população, selecionado para representar suas características de forma adequada. A análise da amostra permite inferências sobre toda a população.
Exemplo: A altura de 35 jovens selecionados aleatoriamente de um total de 200 interessados no programa.
Variáveis
As variáveis são elementos fundamentais na estatística, pois representam as características ou atributos que desejamos estudar em um conjunto de dados. Em um exemplo prático, uma entidade representativa de um bairro realizou uma pesquisa para entender o perfil dos frequentadores de um parque local. Foram coletadas informações sobre características diversas, como sexo, idade, estado civil, frequência semanal no parque e outros aspectos relacionados. Esses elementos que variam de pessoa para pessoa são o que chamamos de variáveis.
Classificação das Variáveis
As variáveis podem ser classificadas em qualitativas e quantitativas, de acordo com o tipo de resposta que oferecem. Vamos entender as diferenças:
- Variáveis Qualitativas
As variáveis qualitativas são aquelas que expressam características ou atributos, sem associação com valores numéricos. Exemplos incluem:- Sexo: Masculino ou Feminino.Estado Civil: Solteiro(a), Casado(a), Separado(a) ou Viúvo(a).Meio de Transporte: Carro, Ônibus ou A pé.
- Variáveis Quantitativas
As variáveis quantitativas são aquelas que expressam quantidades e podem ser representadas numericamente. Dividem-se em dois tipos:- Quantitativas Discretas:
Seus valores são obtidos por contagem e pertencem a um conjunto finito ou enumerável.
Exemplo: A frequência semanal de visitas ao parque. Perceba que para esse valores só podemos ter números naturais como 1, 2, 3, 4, 5, 6 ou 7. - Quantitativas Contínuas:
Seus valores são obtidos por mensuração e pertencem a um intervalo contínuo de números reais.
Exemplos:- Altura: Valores como 1,75; 1,66; ou 1,86 metros.
- Tempo de permanência: Valores como 1 hora e 15 minutos.
- Renda familiar mensal: Valores como 8,9 ou 15,4 salários mínimos.
- Quantitativas Discretas:
Tabela de Dados Coletados no Parque
Para facilitar a compreensão, os dados coletados na pesquisa são apresentados na tabela abaixo, organizada de forma didática e clara:
| Sexo | Idade (anos) | Frequência Semanal | Estado Civil | Meio de Transporte | Tempo de Permanência | Renda Familiar Mensal (em salários mínimos) |
|---|---|---|---|---|---|---|
| Masculino | 26 | 2 | Casado | Carro | 30 min | 13,3 |
| Feminino | 41 | 5 | Viúva | A pé | 2h50min | 8,9 |
| Masculino | 49 | 3 | Separado | A pé | 45 min | 13,9 |
| Feminino | 20 | 4 | Solteira | A pé | 1h20min | 16,0 |
| Masculino | 38 | 3 | Casado | A pé | 2h15min | 9,3 |
| Feminino | 50 | 7 | Casada | A pé | 45 min | 12,4 |
| Masculino | 52 | 2 | Solteiro | A pé | 1h40min | 10,7 |
| Feminino | 41 | 6 | Solteira | Carro | 2h30min | 18,8 |
| Masculino | 31 | 3 | Casado | Ônibus | 2h45min | 7,6 |
Entendendo a Utilidade das Variáveis
As variáveis permitem organizar e analisar os dados de forma estruturada, possibilitando respostas objetivas a questões importantes. Por exemplo:
- Quantas pessoas frequentam o parque mais de 3 vezes por semana?
- Qual é a média de tempo de permanência no parque?
- Qual é o perfil de renda dos frequentadores?
Essas informações, obtidas por meio das variáveis, são a base para realizar análises estatísticas descritivas, como a criação de gráficos e tabelas, e para responder a questões práticas de interesse geral.
Este exemplo prático mostra como as variáveis são essenciais para transformar dados em informações úteis e organizadas.
Exercícios de fixação: Variável Quantitativa e Qualitativa
Exemplo 01: Ao se cadastrar em um site de comércio eletrônico, o usuário deve preencher
um questionário com oito perguntas. Cada uma das questões define uma variável. Classifique-as como qualitativas ou quantitativas.
1) Você tem computador em casa?
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
- Tipo: Qualitativa
- Justificativa: A resposta será categórica, como “Sim” ou “Não”.
[/toggle]
2) Quantas vezes por semana você acessa a Internet?
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
- Tipo: Quantitativa discreta
- Justificativa: O número de vezes é contado e representado por valores inteiros (1, 2, 3, etc.).
[/toggle]
3) Numa escala de zero a 10, qual seu índice de confiança na segurança do comércio eletrônico?
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
- Tipo: Quantitativa discreta
- Justificativa: O índice é representado por valores inteiros entre 0 e 10, obtidos por contagem.
[/toggle]
4) Quantos cartões de crédito você possui?
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
- Tipo: Quantitativa discreta
- Justificativa: O número de cartões é contado e corresponde a valores inteiros.
[/toggle]
5) A residência em que vive é própria ou alugada?
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
- Tipo: Qualitativa
- Justificativa: A resposta será categórica, como “própria” ou “alugada”.
[/toggle]
6) Qual é o provedor que você utiliza para acessar a rede?
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
- Tipo: Qualitativa
- Justificativa: A resposta será categórica, indicando o nome do provedor (ex.: “Vivo”, “Claro”, etc.).
[/toggle]
7) Qual é o tempo médio de acesso à Internet?
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
- Tipo: Quantitativa contínua
- Justificativa: O tempo médio pode assumir valores decimais (ex.: 1,5 horas).
[/toggle]
8) Já comprou algum produto via Internet?
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
- Tipo: Qualitativa
- Justificativa: A resposta será categórica, como “Sim” ou “Não”.
[/toggle]
Exemplo 02: Num cursinho pré-vestibular, os estudantes inscritos responderam a um questionário no qual constavam, entre outras, as seguintes questões:
1 -Qual é a área da carreira universitária pretendida?
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
- Tipo: Qualitativa
- Justificativa: A resposta será categórica, indicando áreas como Saúde, Engenharia, Humanas, etc.
[/toggle]
2 – Você cursou o ensino médio em escola particular ou pública?
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
- Tipo: Qualitativa
- Justificativa: A resposta será categórica, podendo ser “Particular” ou “Pública”.
[/toggle]
3 – Qual é a renda familiar mensal?
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
- Tipo: Quantitativa contínua
- Justificativa: A renda é medida em valores numéricos que podem incluir decimais (ex.: R$ 3.500,50).
[/toggle]
4 – Qual é o grau de escolaridade do chefe da família?
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
- Tipo: Qualitativa
- Justificativa: A resposta será categórica, com níveis como Ensino Fundamental, Médio, Superior, etc.
[/toggle]
5 – Qual é a sua disciplina favorita?
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
- Tipo: Qualitativa
- Justificativa: A resposta será categórica, indicando matérias como Matemática, Português, Física, etc.
[/toggle]
6 – Quantas vezes você já fez cursinho?
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
- Tipo: Quantitativa discreta
- Justificativa: O número de vezes é contado, resultando em valores inteiros (1, 2, 3, etc.).
[/toggle]
7 – Você é usuário da Internet?
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
- Tipo: Qualitativa
- Justificativa: A resposta será categórica, como “Sim” ou “Não”.
[/toggle]
8 – Quanto tempo de estudo diário pretende dedicar ao cursinho?
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
- Tipo: Quantitativa contínua
- Justificativa: O tempo é medido em horas ou minutos, podendo incluir valores decimais (ex.: 2,5 horas).
[/toggle]
Estatística Descritiva
A estatística descritiva é a base para compreender e interpretar conjuntos de dados. Por meio de técnicas que incluem levantamento, organização e representação gráfica, ela transforma dados brutos em informações significativas. Este capítulo explora como organizar e categorizar dados qualitativos e quantitativos, além de definir conceitos fundamentais para a análise estatística.
Levantamento e Organização dos Dados
Antes de qualquer análise estatística, é fundamental realizar o levantamento e a organização dos dados. Isso envolve:
- Definir o objetivo da coleta de dados: Identifique as informações necessárias para responder a uma pergunta ou resolver um problema específico.
- Escolher o método de coleta: Dados podem ser coletados por meio de questionários, entrevistas, experimentos ou registros históricos.
- Classificar os dados: Determine se os dados são qualitativos ou quantitativos, pois isso orientará a forma de organização.
Como Organizar os Dados?
Após a coleta, os dados devem ser organizados em formatos que facilitem sua interpretação. As principais formas de organização incluem:
- Tabelas: Uma tabela resume as informações de forma estruturada, possibilitando a identificação de padrões.
- Gráficos: Representações visuais, como gráficos de barras e setores, tornam os dados mais acessíveis e fáceis de entender.
- Distribuições de Frequência: Agrupar os dados em classes e calcular frequências absolutas e relativas é essencial para analisar grandes conjuntos de dados quantitativos.
Exemplo Prático:
Imagine que um pesquisador queira analisar o perfil de frequentadores de um parque. Após entrevistar 50 pessoas, ele organiza as respostas em uma tabela que classifica variáveis como idade, frequência semanal e meio de transporte. Isso facilita a criação de gráficos e a interpretação dos resultados.
Dados Brutos e Classificação
Os dados brutos são o ponto de partida para a análise estatística. São os valores coletados diretamente de observações ou respostas e que, inicialmente, não possuem organização. Para que esses dados façam sentido, eles precisam ser classificados e organizados.
Definições Importantes:
Dados Brutos: Conjunto de informações coletadas que ainda não foram ordenadas ou organizadas. Exemplo: [8, 5, 12, 7, 5].
Rol: Dados brutos organizados em ordem crescente ou decrescente. Exemplo: [5, 5, 7, 8, 12].
Depois de fazer o Rol, podemos organizar os dados em uma Tabela de Distribuição de Frequência, como no exemplo abaixo para um coleta de dados de 20 pessoas sobre o estado civil.
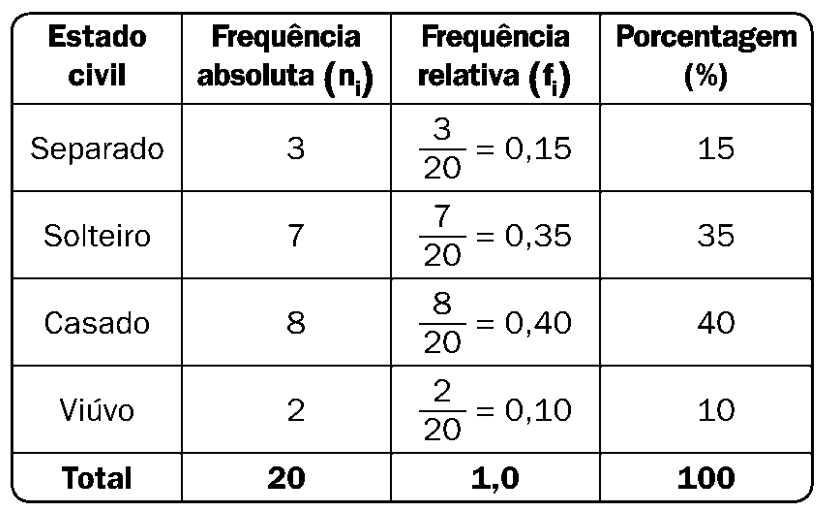
Note que, nesse caso temo uma Variável Quantitativa Discreta, pois temos números inteiros como referência.
Considerando a variável renda mensal familiar, é possível agrupar os dados brutos nas seguintes classes:
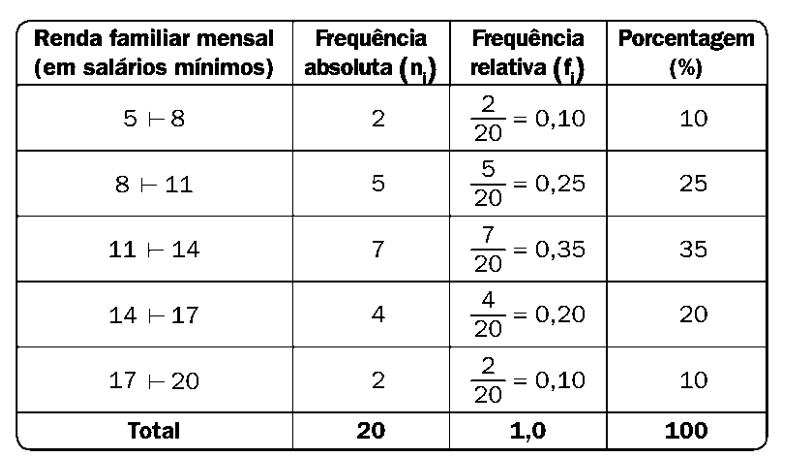
Intervalos de Classes: Divisão dos dados em intervalos, especialmente útil para grandes conjuntos de dados. Cada classe representa um intervalo contínuo.
Exemplo: Para dados da renda familiar, as classes podem ser [5 – 8], [8 – 11], [11 – 14], etc.
Ponto Médio: Valor que representa o centro de cada intervalo de classe. Calculado como a média entre o limite inferior e superior de uma classe.
Fórmula:
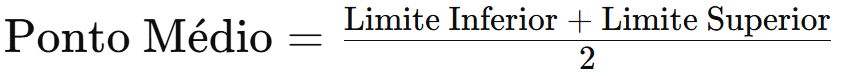
Exemplo: Na classe [5-8], o ponto médio é (5+8)/2 = 6,5
Os intervalos de classe foram definidos considerando:
- Amplitude total dos dados: Variação de 5 a 20 salários mínimos (AT = 20 – 5 = 15).
- Número de classes: Escolheram-se 5 classes para equilibrar detalhamento e simplicidade.
- Amplitude de cada classe: Calculada como AC = AT/número de classes = 15/5 = 3
- Definição dos intervalos: Começam em 5 e somam a amplitude 3, formando:
- [5, 8[, [8, 11[, [11, 14[, etc.
Essa divisão facilita a análise da distribuição de renda, com classes claras e sem sobreposição.
Classificação dos Dados:
Os dados podem ser organizados em:
- Qualitativos: Representam características ou atributos, como gênero ou estado civil.
- Quantitativos: Expressam quantidades e podem ser subdivididos em:
- Discretos: Obtidos por contagem (ex.: número de filhos).
- Contínuos: Obtidos por mensuração (ex.: peso ou altura).
Exemplo Prático:
Suponha que os dados brutos de renda mensal coletados sejam [2500, 3200, 1800, 4000, 2700]. Ao organizá-los em rol: [1800, 2500, 2700, 3200, 4000]. Depois, criamos intervalos de classe: [1000-2000], [2001-3000], etc., calculando o ponto médio de cada intervalo.
A organização e a classificação dos dados são etapas cruciais para tornar a análise estatística eficiente. Essas técnicas são essenciais para identificar padrões, tendências e relações entre variáveis, permitindo decisões baseadas em dados sólidos.
Exemplo 01: Vinte e cinco jovens de até 15 anos foram selecionados para participar de um programa desenvolvido pela Secretaria de Esportes de uma cidade cujo objetivo consiste na formação de futuros jogadores de vôlei. As alturas dos jovens (em metro) são dadas a seguir:
1,82 — 1,77 — 1,79 — 1,74 — 1,73 — 1,81 — 1,82 — 1,69 — 1,71 – 1,78 — 1,78 — 1,88 — 1,72 — 1,65 — 1,75 — 1,78 — 1,73 – 1,82 — 1,84 — 1,74 — 1,76 — 1,79 — 1,83 — 1,76 — 1,70
A partir da menor altura encontrada, agrupe os dados em classes de amplitude 5 cm e faça a tabela de frequência correspondente.
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
O rol (dados organizados em ordem crescente) das alturas dos jovens é:
1.65, 1.69, 1.70, 1.71, 1.72, 1.73, 1.73, 1.74, 1.74, 1.75, 1.76, 1.76, 1.77, 1.78, 1.78, 1.78, 1.79, 1.79, 1.81, 1.82, 1.82, 1.82, 1.83, 1.84, 1.88.
Amplitude total dos dados: 190 − 165 = 25 cm
Número de classes: Escolheu-se 5 classes, resultando em intervalos de mesma amplitude.
Amplitude de cada classe: 25/5 = 5 cm
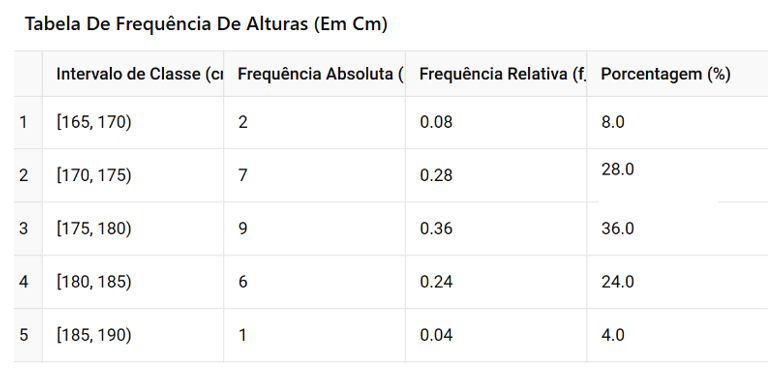
[/toggle]
Frequências Absolutas, Relativas e Acumuladas
Na estatística descritiva, as frequências são fundamentais para organizar, interpretar e visualizar dados. Elas fornecem um resumo claro da distribuição dos valores, permitindo a identificação de padrões e tendências em grandes conjuntos de dados. Neste artigo, abordaremos os conceitos de frequência absoluta, frequência relativa e frequência acumulada, apresentando definições, cálculos e aplicações práticas.
O Que São Frequências na Estatística?
As frequências refletem a distribuição dos dados em termos de contagem, proporção ou acumulação. Essas medidas são usadas para organizar dados em tabelas de frequência, tornando-os mais fáceis de interpretar e analisar.
- Frequência Absoluta (ni): Representa o número de ocorrências de um valor ou intervalo.
- Frequência Relativa (fi): Indica a proporção de uma frequência absoluta em relação ao total de observações.
- Frequência Acumulada (FA): Soma progressiva das frequências absolutas, mostrando quantos valores estão abaixo ou dentro de um determinado limite.
Passos para Construir Frequências
Para ilustrar os conceitos, utilizaremos uma amostra de alturas (em cm) de 35 jovens:
Alturas (cm):
167, 172, 174, 169, 168, 171, 175, 177, 180, 162, 170, 176, 181, 178, 179, 173, 166, 165, 172, 168, 170, 177, 180, 163, 164, 175, 169, 171, 176, 174, 182, 160, 183, 164, 184.
Passo 1: Organizar o Rol
O rol é a organização dos dados em ordem crescente:
Rol (Alturas em ordem crescente):
160, 162, 163, 164, 164, 165, 166, 167, 168, 168, 169, 169, 170, 170, 171, 171, 172, 172, 173, 174, 174, 175, 175, 176, 176, 177, 177, 178, 179, 180, 180, 181, 182, 183, 184.
Passo 2: Determinar a Amplitude Total e Número de Classes
- Amplitude total (AT): Diferença entre o maior e o menor valor: AT = 184−160 = 24 cm
- Número de classes (k): Determinado pela regra de Sturges: k=1+3.3⋅log10(35) ≈ 6
- Amplitude de cada classe (AC): AC = AT/k = 24/6 = 4 cm
Passo 3: Definir os Intervalos de Classe
Os intervalos são definidos a partir do menor valor (160 cm) com amplitude de 4 cm:
- [160, 164)
- [164, 168)
- [168, 172)
- [172, 176)
- [176, 180)
- [180, 184)
Tabela de Frequências
Com os intervalos definidos, calculamos as frequências absolutas (nin_i), relativas (fif_i) e acumuladas (FAFA):
| Intervalo de Classe (cm) | Frequência Absoluta (ni) | Frequência Relativa (fi) | Frequência Acumulada (FA) | Frequência Relativa Acumulada (FRA) |
|---|---|---|---|---|
| [160, 164) | 6 | 6/35 = 0,171 | 6 | 0,171 |
| [164, 168) | 7 | 7/35 = 0,200 | 13 | 0,371 |
| [168, 172) | 8 | 8/35 = 0,229 | 21 | 0,600 |
| [172, 176) | 6 | 6/35 = 0,171 | 27 | 0,771 |
| [176, 180) | 5 | 5/35 = 0,143 | 32 | 0,914 |
| [180, 184) | 3 | 3/35 = 0,086 | 35 | 1,000 |
Explicação das Frequências
- Frequência Absoluta (ni):
É a contagem direta dos dados em cada intervalo. Por exemplo, no intervalo [160, 164), há 6 valores.
- Frequência Relativa (fi):
É a proporção da frequência absoluta em relação ao total de observações (5n = 35).
Exemplo: Para [160, 164):
f1 = 6/35 ≈ 0,171 ou 17,1%
- Frequência Acumulada (FA):
É a soma progressiva das frequências absolutas.
Exemplo: A frequência acumulada até o intervalo [168, 172) é:
FA = 6 + 7 + 8 = 21.
- Frequência Relativa Acumulada (FRA):
É a soma progressiva das frequências relativas. Indica a proporção cumulativa do total de observações.
Exemplo: A frequência relativa acumulada até [168, 172) é:
FRA = 0,171 + 0,200 + 0,229 = 0,600 ou 60%
Gráfico de Barras, Colunas, Setores e Histograma
Os gráficos são ferramentas poderosas para apresentar dados de maneira visual e compreensível. Neste artigo, exploramos quatro tipos de gráficos amplamente utilizados: gráfico de barras, gráfico de colunas, gráfico de setores e pictogramas. Para cada gráfico, apresentamos dados e tabelas correspondentes, destacando suas características e aplicações.
Gráfico de Barras
Definição
O gráfico de barras é usado para representar variáveis qualitativas ou quantitativas discretas. Cada categoria é representada por uma barra cuja altura (ou comprimento) corresponde à frequência ou valor associado.
Exemplo
Uma pesquisa foi realizada em uma escola para identificar a cor preferida dos alunos. Os dados coletados são apresentados na tabela abaixo:
| Cor Preferida | Frequência Absoluta (ni) |
|---|---|
| Azul | 15 |
| Vermelho | 10 |
| Verde | 8 |
| Amarelo | 7 |
| Roxo | 5 |
Descrição dos Dados
- Variável: Cor preferida (qualitativa nominal).
- Frequência Absoluta (ni): Número de alunos que escolheram cada cor como favorita.
Aplicação
No gráfico de barras:
- O eixo horizontal (x) representará as categorias da variável qualitativa (cores preferidas).
- O eixo vertical (y) mostrará as frequências absolutas (ni).
- Cada barra terá uma altura proporcional à frequência da respectiva cor.
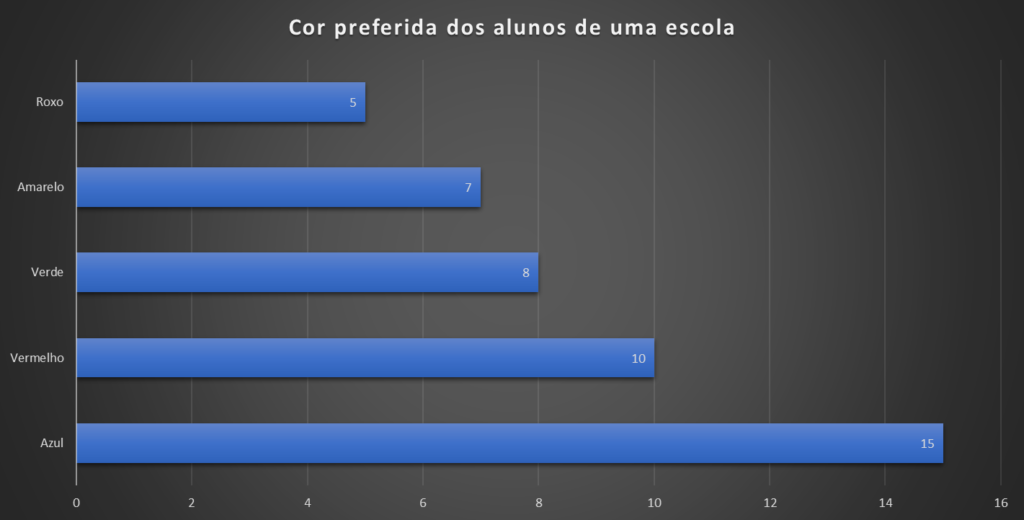
Gráfico de Colunas
Definição
O gráfico de colunas é similar ao de barras, mas as colunas são verticais. É usado para representar dados categóricos ou discretos, facilitando comparações.
Exemplo
Uma empresa realizou uma pesquisa sobre o modo de transporte preferido pelos funcionários para ir ao trabalho. Os resultados são:
| Modo de Transporte | Frequência Absoluta (ni) |
|---|---|
| Carro | 25 |
| Bicicleta | 10 |
| Ônibus | 15 |
| A pé | 8 |
| Moto | 12 |
- Variável: Modo de transporte (qualitativa nominal).
- Aplicação: As categorias (modos de transporte) serão representadas no eixo horizontal, enquanto as frequências correspondentes no eixo vertical.
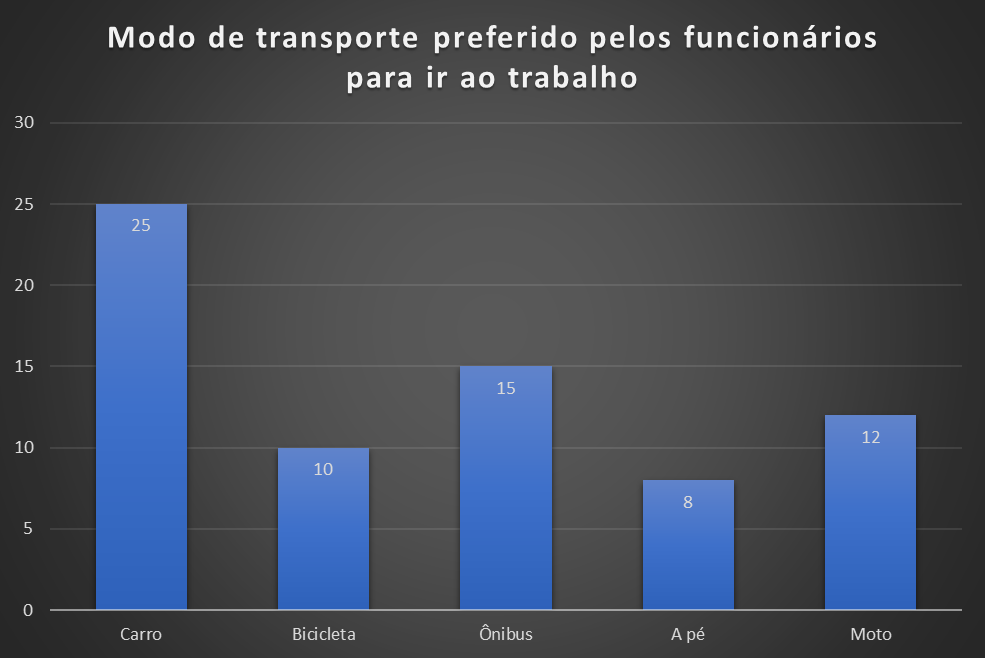
Gráfico de Setores
Definição
O gráfico de setores (ou gráfico de pizza) é usado para representar proporções relativas. Cada segmento do círculo representa uma categoria proporcional ao total.
Exemplo
Um restaurante avaliou a preferência dos clientes pelos tipos de refeição consumidos. Os dados coletados são:
| Tipo de Refeição | Frequência Absoluta (ni) | Frequência Relativa (%) |
|---|---|---|
| Lanches | 40 | 40/120⋅100 = 33,3% |
| Refeições Completas | 50 | 50/120⋅100 = 41,7% |
| Sobremesas | 20 | 20/120⋅100 = 16,7% |
| Bebidas | 10 | 10/120⋅100 = 8,3% |
- Variável: Tipo de refeição (qualitativa nominal).
- Aplicação: O gráfico de setores mostrará as proporções das categorias em relação ao total.
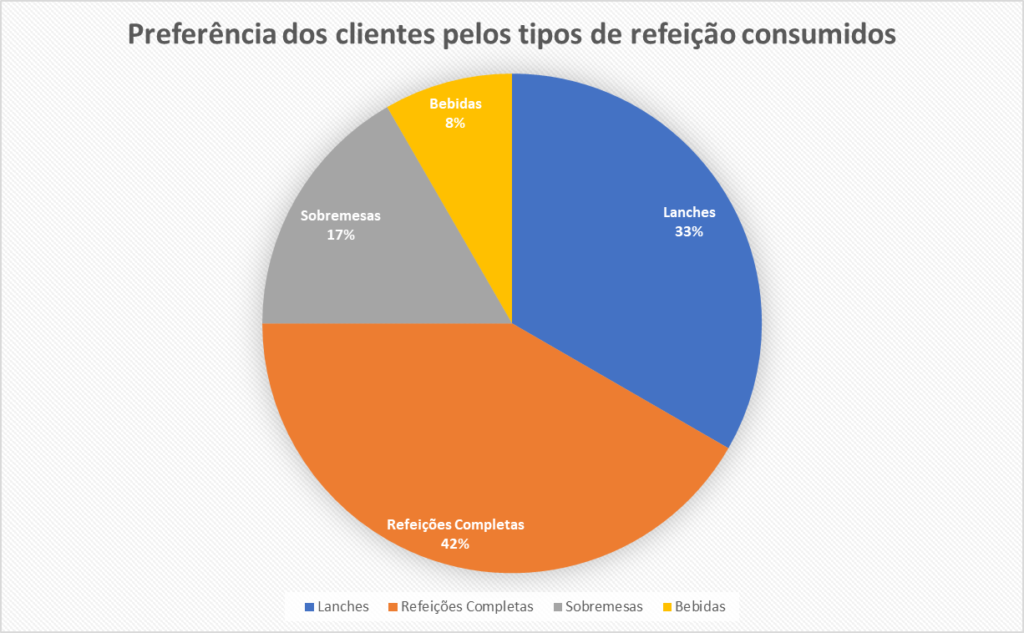
Gráfico Histograma
Um histograma é uma representação gráfica de dados quantitativos que utiliza barras retangulares para ilustrar a frequência de valores ou intervalos em um conjunto de dados. Cada barra do histograma corresponde a um intervalo de classe, e a altura da barra reflete a frequência absoluta, relativa ou percentual dos dados naquele intervalo.
Cenário
Uma pesquisa foi realizada para medir o tempo diário gasto em atividades de lazer por 50 pessoas, em minutos. Os tempos coletados são os seguintes (em minutos):
Dados Brutos (em minutos):
45, 30, 50, 65, 40, 35, 60, 55, 70, 80, 75, 50, 45, 90, 85, 95, 100, 110, 115, 120, 50, 55, 65, 70, 75, 80, 85, 90, 95, 60, 40, 35, 30, 25, 20, 15, 50, 55, 60, 45, 30, 25, 20, 15, 10, 5, 100, 105, 110, 115.
Passo 1: Organizar os Dados em Rol
Os dados organizados em ordem crescente:
Rol:
5, 10, 15, 15, 20, 20, 25, 25, 30, 30, 30, 35, 35, 40, 40, 45, 45, 45, 50, 50, 50, 50, 55, 55, 55, 60, 60, 60, 65, 65, 70, 70, 75, 75, 75, 80, 80, 85, 85, 85, 90, 90, 95, 95, 100, 100, 105, 110, 110, 115.
Passo 2: Determinar a Amplitude Total e Número de Classes
Amplitude Total (AT):
AT = Maior valor − Menor valor = 115 − 5 = 110 minutos
Número de Classes (k):
Usando a regra de Sturges:
k = 1 + 3.3⋅log10(50) ≈ 1 + 3.3⋅1.698 = 6.6
Arredondamos para 7 classes.
Amplitude de Cada Classe (AC):
AC = AT/k = 110/7 ≈ 15,7 minutos
Arredondamos para 16 minutos.
Passo 3: Definir os Intervalos de Classe
Os intervalos são definidos a partir do menor valor (5 minutos) e incrementam pela amplitude de classe (16 minutos):
- [5, 21)
- [21, 37)
- [37, 53)
- [53, 69)
- [69, 85)
- [85, 101)
- [101, 117)
Passo 4: Contar as Frequências Absolutas
A contagem dos dados em cada intervalo:
| Intervalo de Classe (min) | Frequência Absoluta (ni) |
|---|---|
| [5, 21) | 8 |
| [21, 37) | 7 |
| [37, 53) | 9 |
| [53, 69) | 10 |
| [69, 85) | 8 |
| [85, 101) | 5 |
| [101, 117) | 3 |
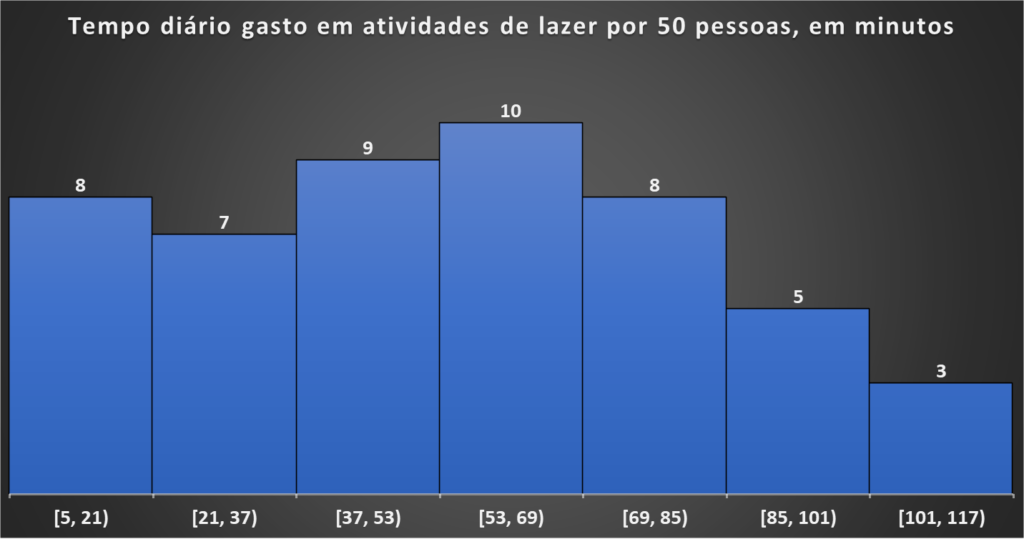
Tabela de Frequências
| Intervalo (min) | Frequência Absoluta (ni) | Frequência Relativa (fi) | Porcentagem (%) |
|---|---|---|---|
| [5, 21) | 8 | 8/50 = 0,16 | 16,0 |
| [21, 37) | 7 | 7/50 = 0,14 | 14,0 |
| [37, 53) | 9 | 9/50 = 0,18 | 18,0 |
| [53, 69) | 10 | 10/50 = 0,20 | 20,0 |
| [69, 85) | 8 | 8/50 = 0,16 | 16,0 |
| [85, 101) | 5 | 5/50 = 0,10 | 10,0 |
| [101, 117) | 3 | 3/50=0,06 | 6,0 |
Estatística: Tendência Central e Dispersão
A estatística descritiva é fundamental para resumir, interpretar e comparar conjuntos de dados. Neste artigo, abordaremos os principais conceitos relacionados às médias, medidas de tendência central (mediana e moda) e medidas de dispersão (amplitude total, desvio médio, variância, desvio padrão e coeficiente de variação).
1. Médias
As médias são medidas de tendência central que fornecem uma visão geral de um conjunto de dados.
1.1. Média Aritmética
A média aritmética é calculada somando todos os valores de um conjunto de dados e dividindo pelo número total de observações (n):
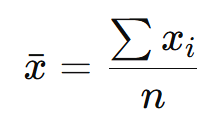
Obs: ∑ é o somatório de todos os valores.
Exemplo:
Os números 5, 7, 8 têm média:
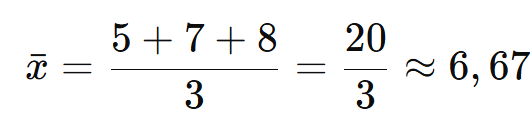
1.2. Média Aritmética de Distribuição de Frequências ou Ponderada
Quando os dados estão organizados em uma tabela de frequências, a média é calculada utilizando:
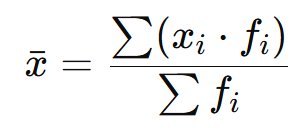
- xi: Valor do intervalo ou ponto médio.
- fi: Frequência absoluta.
Exemplo:
| Valor (xi) | Frequência (fi) | xi⋅fi |
|---|---|---|
| 2 | 3 | 6 |
| 4 | 5 | 20 |
| 6 | 2 | 12 |

1.3. Média Geométrica
A média geométrica é utilizada para conjuntos de dados positivos, sendo definida como a raiz nn-ésima do produto dos valores:
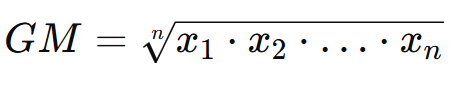
Exemplo:
Para os valores 3, 9 e 27:
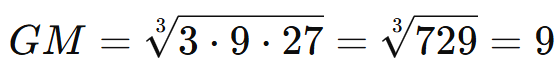
1.4. Média Harmônica
A média harmônica é útil quando os dados são taxas ou razões:
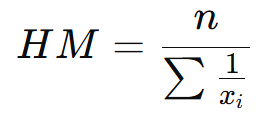
Exemplo:
Para 2, 4 e 6:
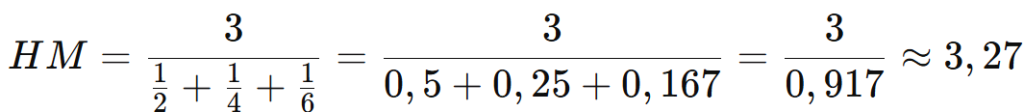
1.5. Média Ponderada
A média ponderada é utilizada quando os valores possuem pesos diferentes (pi):
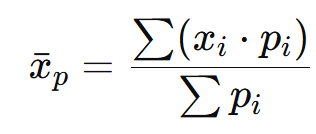
Exemplo:
Notas de 6, 8 e 9 com pesos 2, 3 e 5:
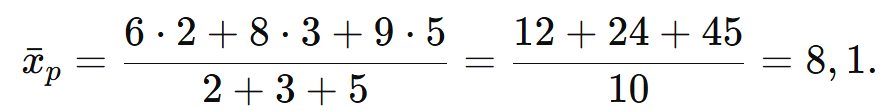
2. Medidas de Tendência Central
2.1. Mediana
A mediana é o valor central de um conjunto de dados ordenados. Se nn for ímpar, a mediana é o valor do meio; se nn for par, é a média dos dois valores centrais.
Exemplo:
Para 3, 5, 7, 9, a mediana é:
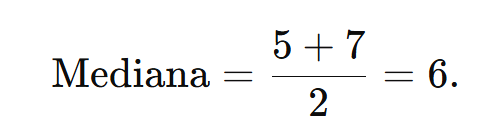
2.2. Moda
A moda é o valor ou intervalo mais frequente em um conjunto de dados.
Exemplo:
No conjunto 2, 3, 3, 4, 5, a moda é 3.
3. Medidas de Dispersão
3.1. Amplitude Total
A amplitude total é a diferença entre o maior e o menor valor do conjunto de dados:
AT = Maior valor − Menor valor
Exemplo:
Para 10, 15, 20:
AT = 20 − 10 = 10
3.2. Desvio Médio
O desvio médio é a média dos desvios absolutos em relação à média aritmética:
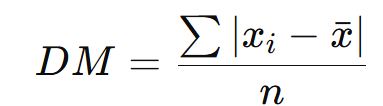
Exemplo:
Para 2, 4, 6
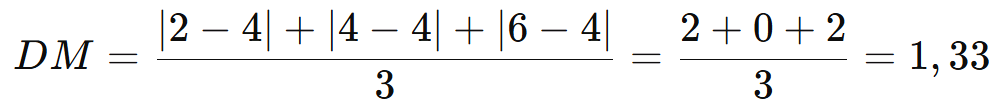
3.3. Variância
A variância mede a dispersão dos dados em relação à média:
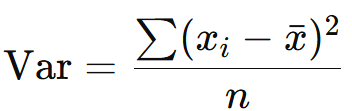
Exemplo:
Para 2, 4, 6 (xˉ=4):
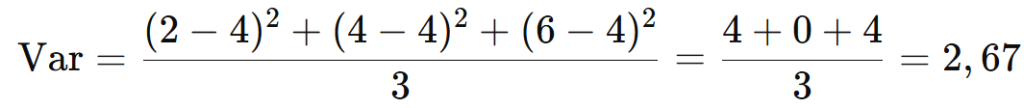
3.4. Desvio Padrão
O desvio padrão é a raiz quadrada da variância:
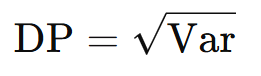
Exemplo:
Para Var=2,67
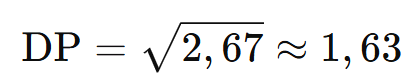
3.5. Coeficiente de Variação
O coeficiente de variação (CV) é dado pela razão entre o desvio padrão e a média, expressa em porcentagem:
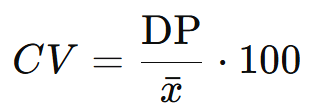
Exemplo:
Com DP = 1,63 e xˉ = 4:
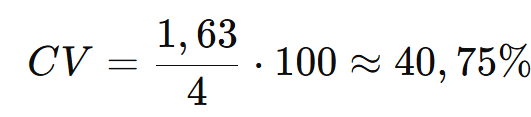
4. Conclusão
As médias, medidas de tendência central e dispersão são ferramentas essenciais para analisar e interpretar conjuntos de dados. Elas ajudam a resumir informações e compreender como os valores se distribuem em relação a uma referência central, possibilitando comparações e tomadas de decisão fundamentadas.

























