Pratique e domine análise combinatória com este exercícios resolvidos passo a passo! Explore conceitos fundamentais da matemática, como permutação, combinação e arranjo, de forma clara e objetiva. Baixe o PDF com exercícios de análise combinatória e tenha uma ferramenta completa para estudar offline e se preparar para provas e concursos.
Questão de Analise Combinatória – Princípio Fundamental da Contagem
As letras em código morse são formadas por sequências de traços (–) e pontos ( ⋅ ), sendo permitidas repetições. Por exemplo: (–; ⋅; –; –; ⋅; ⋅). Quantas letras podem ser representadas:
a) usando exatamente 3 símbolos?
b) usando no máximo 8 símbolos?
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
1 – Análise Combinatória – Princípio Fundamental da Contagem
Este problema utiliza o Princípio Fundamental da Contagem, pois cada símbolo em um código morse pode ser um traço (–) ou um ponto (⋅). Vamos calcular o número de combinações possíveis para as duas condições:
a) usando exatamente 3 símbolos e
b) usando no máximo 8 símbolos.
2 – Entendendo o Enunciado
O enunciado informa:
- Cada símbolo pode ser – ou ⋅ (2 opções).
- Repetições são permitidas.
- Precisamos calcular:
- a) O número de combinações possíveis com 3 símbolos.
- b) O número de combinações possíveis com até 8 símbolos.
3 – Cálculo
a) Usando exatamente 3 símbolos
Cada posição pode ser preenchida com 2 opções (– ou ⋅). Para 3 posições, o número total de combinações é dado por:
Total de combinações = 23
Calculando:
23 = 2×2×2 = 8
Portanto, é possível formar 8 códigos diferentes usando exatamente 3 símbolos.
b) Usando no máximo 8 símbolos
Neste caso, consideramos todas as combinações possíveis com 1, 2, 3, …, até 8 símbolos. O total de combinações para cada número de símbolos é dado por:
Total para n símbolos = 2n
O total acumulado para n = 1 até n = 8 é:
Total geral = 21 + 22 + 23 +⋯+ 28
Essa soma é uma progressão geométrica com razão r = 2, termo inicial a = 21, e 8 termos. A soma de uma PG é dada por:

Substituímos os valores:
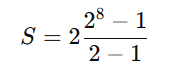
S = 2×(256−1) = 2×255 = 510
Portanto, é possível formar 510 códigos diferentes usando no máximo 8 símbolos.
4 – Resposta
a) É possível formar 8 códigos diferentes usando exatamente 3 símbolos.
b) É possível formar 510 códigos diferentes usando no máximo 8 símbolos.
Gostou dessa questão de? Que tal desafiar ainda mais seus conhecimentos acessando mais uma questão matemática? 📚✨
[/toggle]
📘 Quer dominar a análise combinatória? Adquira agora nosso PDF completo com exercícios resolvidos passo a passo e eleve seu aprendizado!
📚 Quer aprofundar seus conhecimentos em Análise Combinatória e Probabilidade? Confira nossa recomendação dos melhores livros sobre o tema com exercícios resolvidos e dicas práticas. 👉Os melhores livros de Analise Combinatória e Probabilidade

























