A fórmula de permutação é uma das ferramentas mais importantes da análise combinatória, usada para calcular o total de maneiras de organizar elementos distintos ou repetidos. Permutações aparecem frequentemente em problemas de organização, estatística e probabilidade, sendo fundamentais para estudantes e profissionais. Neste artigo, exploraremos as diferentes fórmulas de permutação, exemplos práticos e suas aplicações, no conjunto de todas as fórmulas matemática.
O Que É Permutação?
A permutação é o arranjo de elementos de um conjunto em uma ordem específica. Existem dois tipos principais:
- Permutação Simples: Todos os elementos são distintos.
- Permutação com Repetição: Alguns elementos se repetem dentro do conjunto.
A fórmula utilizada depende do tipo de permutação envolvida.
Fórmula de Permutação Simples
A permutação simples calcula o total de maneiras de organizar nn elementos distintos. A fórmula é:
Pn = n!
Onde:
- Pn é o total de permutações.
- n!(lê-se “n fatorial”) é o produto de todos os números inteiros positivos até n.
Exemplo Prático: Quantas formas diferentes existem para organizar as letras da palavra “CASA” (sem considerar repetições)?
P4 = 4! = 4×3×2×1 = 24
Resposta: Existem 24 organizações diferentes.
Confira também as fórmulas de geometria plana
Fórmula de Permutação com Repetição
Se alguns elementos se repetem, a fórmula é ajustada para levar em conta as repetições:
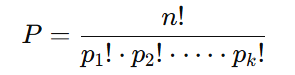
Onde:
- n!: Total de elementos.
- p1!, p2! ,…, pk!: Fatoriais das repetições de cada elemento.
Exemplo Prático: Quantas formas existem de organizar as letras da palavra “BANANA”?
P = 6!/(3!⋅2!) = 720/12 = 60
Resposta: Existem 60 organizações diferentes.
Confira também as formulas geometria espacial
Diferença Entre Permutação e Arranjo
Embora ambas envolvam organização, a permutação utiliza todos os elementos do conjunto, enquanto o arranjo considera apenas uma parte deles. A fórmula do arranjo é:
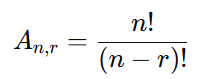
Dicas para Memorizar e Usar a Fórmula de Permutação
- Pratique Regularmente: Resolva questões que envolvam diferentes tipos de permutações.
- Entenda os Conceitos: Distinga claramente entre permutações simples e com repetição.
- Use Representações Visuais: Organize os elementos em diagramas para facilitar a compreensão.
Confira também a fórmula de Bhaskara
Aplicações da Fórmula de Permutação
A fórmula permutação é amplamente usada em diversas áreas, como:
- Concursos e Vestibulares: Questões de organização e combinação de elementos.
- Estatística e Probabilidade: Cálculo de eventos prováveis.
- Computação: Análise de dados e algoritmos.
- Planejamento: Organização de tarefas e criação de cronogramas.
Exercício Prático
Problema: Quantas formas diferentes podem ser organizadas as letras da palavra “CIRCO”?
- Total de letras: n = 5.
- Repetições: A letra “C” aparece 2 vezes.
A fórmula será:
P = 5!/2! = 120/2 = 60
Resposta: Existem 60 organizações diferentes.
Conclusão
A fórmula permutação das fórmulas matemática é essencial para resolver problemas que envolvam organização de elementos, sendo uma ferramenta indispensável em diversas situações acadêmicas e profissionais, veja mais em nosso Canal do WhatsApp. Compreender os conceitos e praticar regularmente é a melhor maneira de dominar essa técnica. Continue explorando e aplicando a matemática para resolver desafios com precisão e confiança!














