Explore uma seleção completa com 18 questões resolvidas sobre funções matemáticas, ideais para o ensino fundamental, médio e preparatórios para concursos.
Nesta coletânea você encontrará problemas com gráficos, tabelas, contextos reais (como velocidade, perímetro, consumo e experiências) e funções afins aplicadas ao dia a dia. Cada questão conta com uma explicação clara, passo a passo e com interpretação de enunciado, facilitando a compreensão de temas como:
- Função do 1º grau e função afim
- Proporcionalidade direta
- Construção de fórmulas
- Interpretação de tabelas e gráficos
- Aplicações em contextos do ENEM e provas institucionais
Ideal para revisar conteúdos, preparar aulas, praticar com estudantes ou reforçar seus estudos com foco em interpretação e raciocínio matemático.
🧠 Mapas Mentais de MatemáticaConteúdo: Função afim aplicada ao cotidiano – Conversão de medidas em numeração
Karina trabalha em um ateliê que confecciona sapatos e usa uma fórmula para calcular a numeração deles, de acordo com a medida de comprimento dos pés dos clientes.🟪 Os profissionais que trabalham na confecção de sapatos sob medida utilizam técnica e criatividade na criação dos modelos.
A fórmula utilizada por Karina é dada por:
$$ y = 1{,}25x + 7 $$
em que \( y \) é a numeração do sapato e \( x \), a medida de comprimento do pé, em centímetro. Quando o resultado não é um número natural, ela o arredonda para o número natural imediatamente maior do que o valor calculado.
a) Determine a numeração do sapato de um cliente de Karina cujo pé mede 27 cm.
b) Considere, agora, sua numeração de sapato e utilize essa fórmula para calcular a medida de comprimento \( x \) correspondente. Depois, use uma régua para medir o comprimento do seu pé e confira se o valor calculado é um valor aproximado da medida verificada. (Resposta pessoal.)
🔍 Ver solução passo a passo
a) Determinar a numeração do sapato para um pé de 27 cm:
A fórmula é:
$$ y = 1{,}25 \cdot 27 + 7 $$
$$ y = 33{,}75 + 7 = 40{,}75 $$
Como não é um número natural, devemos arredondar para o número natural imediatamente superior:
$$ \boxed{41} $$
b) Atividade prática:
Use a fórmula ao contrário: dado um número de sapato (por exemplo, 41), calcule o valor de \( x \) e compare com a medida real do seu pé com uma régua.
Reescrevendo a fórmula:
$$ x = \frac{y – 7}{1{,}25} $$
Se \( y = 41 \):
$$ x = \frac{41 – 7}{1{,}25} = \frac{34}{1{,}25} = 27{,}2 \text{ cm} $$
Compare com sua medida real e veja se é próxima.
✅ Conclusão:
- a) Numeração do sapato para 27 cm: 41
- b) Atividade pessoal: calcular e comparar com medida real do pé
Conteúdo: Função Afim – Identificação, Classificação e Coeficientes
Considere as funções reais definidas a seguir:- I. \( f(x) = 3x^2 – 5x + 4 \)
- II. \( g(x) = -2x + \sqrt{3} \)
- III. \( h(x) = \dfrac{2}{5}x \)
- IV. \( i(x) = 0{,}01 \)
a) Qual(is) dessas leis é(são) de função afim?
b) Classifique as funções afins em função polinomial do 1º grau, função linear e/ou função constante.
c) Para as funções afins, identifique os valores dos coeficientes \( a \) e \( b \).
🔍 Ver solução passo a passo
a) Qual(is) dessas leis é(são) de função afim?
Uma função afim tem a forma geral: $$ f(x) = ax + b $$ ou seja, é uma função polinomial de grau 1. Vamos analisar cada item:
- I. \( f(x) = 3x^2 – 5x + 4 \): não é função afim, pois é do 2º grau.
- II. \( g(x) = -2x + \sqrt{3} \): é função afim, está na forma \( ax + b \).
- III. \( h(x) = \dfrac{2}{5}x \): é função afim, está na forma \( ax \) (com \( b = 0 \)).
- IV. \( i(x) = 0{,}01 \): é função afim, uma constante (com \( a = 0 \)).
Resposta: II, III e IV são funções afins.
b) Classifique as funções afins:
- II. \( g(x) = -2x + \sqrt{3} \) → Função polinomial do 1º grau
- III. \( h(x) = \dfrac{2}{5}x \) → Função linear (sem termo independente)
- IV. \( i(x) = 0{,}01 \) → Função constante (sem variável)
c) Coeficientes \( a \) e \( b \) das funções afins:
- II. \( a = -2 \), \( b = \sqrt{3} \)
- III. \( a = \dfrac{2}{5} \), \( b = 0 \)
- IV. \( a = 0 \), \( b = 0{,}01 \)
✅ Conclusão:
- Funções afins: II, III e IV
- Classificação:
- II → função polinomial do 1º grau
- III → função linear
- IV → função constante
- Coeficientes:
- II: \( a = -2 \), \( b = \sqrt{3} \)
- III: \( a = \dfrac{2}{5} \), \( b = 0 \)
- IV: \( a = 0 \), \( b = 0{,}01 \)
Conteúdo: Função afim – cálculo de imagem e raiz
Dada a função definida por:$$ f(x) = 5x – 2 $$
determine:
a) \( f(2) \)
b) O valor de \( x \) para o qual \( f(x) = 0 \)
🔍 Ver solução passo a passo
a) Calcular \( f(2) \):
Substituímos \( x = 2 \) na expressão da função:
$$ f(2) = 5 \cdot 2 – 2 = 10 – 2 = 8 $$
Resposta: \( \boxed{8} \)
b) Determinar \( x \) para \( f(x) = 0 \):
Igualamos a função a zero:
$$ 5x – 2 = 0 $$
Somamos 2 dos dois lados:
$$ 5x = 2 $$
Dividindo ambos os lados por 5:
$$ x = \frac{2}{5} $$
Resposta: \( \boxed{\frac{2}{5}} \)
✅ Conclusão:
- a) \( f(2) = 8 \)
- b) \( x = \dfrac{2}{5} \)
Conteúdo: Função afim – aplicação prática com taxa fixa e variável
(Enem/MEC) Para concretar a laje de sua residência, uma pessoa contratou uma construtora. Tal empresa informa que o preço \( y \) do concreto bombeado é composto de duas partes: uma fixa, chamada de taxa de bombeamento, e uma variável, que depende do volume \( x \) de concreto utilizado.Sabe-se que a taxa de bombeamento custa R$ 500,00 e que o metro cúbico do concreto bombeado é de R$ 250,00.
A expressão que representa o preço \( y \), em função do volume \( x \), em metro cúbico, é:
-
a) \( y = 250x \)
b) \( y = 500x \)
c) \( y = 750x \)
d) \( y = 250x + 500 \)
e) \( y = 500x + 250 \)
🔍 Ver solução passo a passo
🔎 Entendendo o enunciado:
Temos um valor fixo de R$ 500,00 (taxa de bombeamento) e um valor variável que depende do volume de concreto utilizado: R$ 250,00 por metro cúbico.
1) Montando a função:
O valor total \( y \) pode ser calculado com:
$$ y = 250x + 500 $$
Onde:
- \( 250x \) representa o custo variável conforme o volume \( x \)
- \( 500 \) representa o custo fixo
2) Analisando as alternativas:
A única que representa corretamente essa função é:
Alternativa d) \( y = 250x + 500 \)
✅ Conclusão:
- Expressão correta: \( \boxed{y = 250x + 500} \)
- Alternativa correta: d)
Conteúdo: Função afim – determinar a lei a partir de dois pontos
Considere uma função afim dada por \( y = h(x) \). Sabendo que:- \( h(1) = 4 \)
- \( h(-2) = 10 \)
Escreva a lei da função \( h \) e calcule:
$$ h\left(-\dfrac{1}{2}\right) $$
🔍 Ver solução passo a passo
🔎 Etapa 1 – Modelo da função afim:
Seja \( h(x) = ax + b \). Vamos usar os pontos fornecidos para montar um sistema:
- Se \( h(1) = 4 \), então: $$ a \cdot 1 + b = 4 \Rightarrow a + b = 4 \quad \text{(1)} $$
- Se \( h(-2) = 10 \), então: $$ a \cdot (-2) + b = 10 \Rightarrow -2a + b = 10 \quad \text{(2)} $$
🔎 Etapa 2 – Resolvendo o sistema de equações:
Temos o sistema:
(1) \( a + b = 4 \)
(2) \( -2a + b = 10 \)
Subtraindo a equação (1) da equação (2):
\( (-2a + b) – (a + b) = 10 – 4 \)
\( -2a + b – a – b = 6 \)
\( -3a = 6 \Rightarrow a = -2 \)
Substituindo o valor de \( a \) na equação (1):
\( -2 + b = 4 \Rightarrow b = 6 \)
🔎 Etapa 3 – Encontrando a expressão da função:
Com os valores encontrados, temos:
$$ h(x) = -2x + 6 $$
🔎 Etapa 4 – Cálculo de \( h\left(-\dfrac{1}{2}\right) \):
Substituindo na função:
$$ h\left(-\dfrac{1}{2}\right) = -2 \cdot \left(-\dfrac{1}{2}\right) + 6 $$
$$ h\left(-\dfrac{1}{2}\right) = 1 + 6 = 7 $$
✅ Conclusão:
- Lei da função: \( h(x) = -2x + 6 \)
- Valor de \( h\left(-\dfrac{1}{2}\right) \): \( \boxed{7} \)
Conteúdo: Função do 1º grau – Cálculo proporcional e interpretação de fórmulas
Sofia quer produzir folhetos com a propaganda de sua empresa.Na gráfica A, o valor da impressão desse folheto, por unidade, é R$ 0,30.
Na gráfica B, o valor, também por unidade, é R$ 0,25.
a) Escreva a fórmula que relaciona o valor \( y \) a ser pago pela impressão, em reais, com o número \( x \) de folhetos impressos em cada uma dessas gráficas.
b) Na gráfica A, o valor pago pela impressão é diretamente proporcional ao número de unidades impressas? E na gráfica B? Justifique.
c) Se Sofia encomendar 1000 folhetos na gráfica B, quantos reais gastará?
🔍 Ver solução passo a passo
a) Fórmulas das funções:
- Gráfica A: $$ y_A = 0{,}30x $$
- Gráfica B: $$ y_B = 0{,}25x $$
b) Verificando proporcionalidade direta:
Funções do tipo \( y = ax \) representam proporcionalidade direta entre as variáveis.
- Gráfica A: é diretamente proporcional, pois não possui termo constante.
- Gráfica B: também é diretamente proporcional, pois também está na forma \( y = ax \).
c) Cálculo do custo na gráfica B:
Se Sofia encomendar 1000 folhetos:
$$ y_B = 0{,}25 \cdot 1000 = 250 $$
Resposta: R$ 250,00
✅ Conclusão:
- Fórmulas: \( y_A = 0{,}30x \), \( y_B = 0{,}25x \)
- Ambas são funções diretamente proporcionais
- Valor gasto com 1000 folhetos na gráfica B: R$ 250,00
Conteúdo: Função linear – cálculo por proporcionalidade
Sabendo que \( f \) é uma função linear e que:$$ f(-3) = 4 $$
determine o valor de \( f(6) \).
🔍 Ver solução passo a passo
🔎 Entendendo o conceito:
Uma função linear tem a forma:
$$ f(x) = ax $$
Ou seja, ela passa pela origem e não possui termo constante.
1) Usando a informação \( f(-3) = 4 \):
Substituímos na expressão:
$$ a \cdot (-3) = 4 \Rightarrow a = -\dfrac{4}{3} $$
2) Calculando \( f(6) \):
Agora usamos o valor de \( a \) para calcular:
$$ f(6) = -\dfrac{4}{3} \cdot 6 = -8 $$
✅ Conclusão:
- Coeficiente angular: \( a = -\dfrac{4}{3} \)
- Função: \( f(x) = -\dfrac{4}{3}x \)
- Valor de \( f(6) \): \( \boxed{-8} \)
Conteúdo: Função afim aplicada ao perímetro de figuras planas
Os lados de um retângulo medem \( x \) e \( x+5 \), em metros.a) Escreva a fórmula matemática que relaciona o perímetro \( p \) com a medida \( x \).
b) Reproduza a tabela abaixo e complete os valores de \( p \):
| \( x \) (em metro) | 5 | 10 | 20 | 30 | ? | ? |
|---|---|---|---|---|---|---|
| \( p \) (em metro) | 40 | 60 | 100 | 140 | 162 | 210 |
c) As grandezas \( p \) e \( x \) são diretamente proporcionais? Justifique.
d) Quais devem ser as medidas dos lados desse retângulo para que o perímetro seja de 78 metros?
🔍 Ver solução passo a passo
a) Fórmula do perímetro:
Os lados do retângulo são \( x \) e \( x + 5 \). O perímetro é a soma dos quatro lados:
$$ p = 2x + 2(x + 5) = 2x + 2x + 10 = 4x + 10 $$
b) Completando a tabela:
Usamos a fórmula \( p = 4x + 10 \):
- Para \( x = 5 \): \( p = 4(5) + 10 = 30 \)
- Para \( x = 10 \): \( p = 4(10) + 10 = 50 \)
- Para \( x = 20 \): \( p = 4(20) + 10 = 90 \)
- Para \( x = 30 \): \( p = 4(30) + 10 = 130 \)
- Para \( p = 162 \): $$ 162 = 4x + 10 \Rightarrow 4x = 152 \Rightarrow x = 38 $$
c) As grandezas \( p \) e \( x \) são diretamente proporcionais?
Não. Para que duas grandezas sejam diretamente proporcionais, a razão entre elas deve ser constante:
$$ \frac{p}{x} = \frac{4x + 10}{x} = 4 + \frac{10}{x} $$
Como \( \frac{10}{x} \) varia com \( x \), a razão \( \frac{p}{x} \) não é constante. Logo, não há proporcionalidade direta.
d) Qual deve ser o valor de \( x \) para que o perímetro seja 78 metros?
Resolvemos a equação:
$$ 78 = 4x + 10 \Rightarrow 4x = 68 \Rightarrow x = 17 $$
O outro lado será \( x + 5 = 17 + 5 = 22 \).
Resposta: As medidas dos lados devem ser 17 m e 22 m.
✅ Conclusão:
- Fórmula do perímetro: \( p = 4x + 10 \)
- Valores completos da tabela: \( x = 38 \) para \( p = 162 \), e \( x = 50 \) para \( p = 210 \)
- Proporcionalidade: \( p \) e \( x \) não são diretamente proporcionais
- Para \( p = 78 \): lados de 17 m e 22 m
Conteúdo: Função polinomial do 1º grau – determinação da lei por dois pontos
(FGV-SP) Uma função polinomial \( f \) do 1º grau é tal que:- \( f(3) = 6 \)
- \( f(4) = 8 \)
Portanto, o valor de \( f(10) \) é:
- a) 16
- b) 17
- c) 18
- d) 19
- e) 20
🔍 Ver solução passo a passo
🔎 Etapa 1 – Considerar a forma geral da função:
A função polinomial do 1º grau tem a forma:
$$ f(x) = ax + b $$
🔎 Etapa 2 – Usar os dois pontos fornecidos:
- Se \( f(3) = 6 \), então: $$ 3a + b = 6 \quad \text{(1)} $$
- Se \( f(4) = 8 \), então: $$ 4a + b = 8 \quad \text{(2)} $$
Subtraindo (2) – (1):
$$ (4a + b) – (3a + b) = 8 – 6 \Rightarrow a = 2 $$
Substituindo em (1):
$$ 3 \cdot 2 + b = 6 \Rightarrow 6 + b = 6 \Rightarrow b = 0 $$
🔎 Etapa 3 – Função final e cálculo:
A função é:
$$ f(x) = 2x $$
Logo:
$$ f(10) = 2 \cdot 10 = \boxed{20} $$
✅ Conclusão:
- Função encontrada: \( f(x) = 2x \)
- Valor de \( f(10) \): \( \boxed{20} \)
- Alternativa correta: e)
Conteúdo: Função do 1º grau – movimento uniforme com velocidade constante
Considere que uma pessoa, caminhando a uma velocidade constante, percorra, em média, 80 centímetros a cada 1 segundo.a) Escreva a fórmula que indica a distância percorrida \( d \), em centímetros, em função do tempo \( t \), em segundos.
b) Nessa situação, as grandezas \( d \) e \( t \) são diretamente proporcionais? Justifique sua resposta.
c) Quantos metros essa pessoa percorrerá em 10 segundos? E em 40 segundos?
d) Quantos segundos essa pessoa levará para percorrer 100 metros?
🔍 Ver solução passo a passo
a) Fórmula da função:
Sabemos que a pessoa percorre 80 cm a cada segundo. Logo:
$$ d = 80t $$
b) Proporcionalidade entre \( d \) e \( t \):
A fórmula tem a forma \( d = 80t \), ou seja, é uma função linear do tipo \( y = ax \), com coeficiente fixo e sem termo independente. Logo:
Sim, as grandezas são diretamente proporcionais.
c) Distância percorrida em metros:
- Em 10 segundos: $$ d = 80 \cdot 10 = 800 \text{ cm} = 8 \text{ m} $$
- Em 40 segundos: $$ d = 80 \cdot 40 = 3200 \text{ cm} = 32 \text{ m} $$
d) Tempo necessário para percorrer 100 metros:
100 metros = 10000 cm. Usamos a fórmula \( d = 80t \):
$$ 10000 = 80t \Rightarrow t = \frac{10000}{80} = 125 \text{ s} $$
✅ Conclusão:
- Função: \( d = 80t \)
- As grandezas \( d \) e \( t \) são diretamente proporcionais: Sim
- Distância em 10 segundos: 800 cm = 8 m
- Distância em 40 segundos: 3200 cm = 32 m
- Tempo para percorrer 100 metros: 125 segundos
Conteúdo: Função afim – sistema com condições e equação auxiliar
(UFC-CE) Seja \( f \) uma função real, de variável real, definida por:$$ f(x) = ax + b $$
Sabendo que:
- \( f(1) = -9 \)
- \( b^2 – a^2 = 54 \)
Calcule o valor de \( a – b \).
🔍 Ver solução passo a passo
🔎 Etapa 1 – Substituir \( f(1) = -9 \) na função:
Sabemos que \( f(x) = ax + b \), então:
$$ f(1) = a(1) + b = -9 \Rightarrow a + b = -9 \quad \text{(1)} $$
🔎 Etapa 2 – Usar a equação adicional:
Temos também:
$$ b^2 – a^2 = 54 \quad \text{(2)} $$
Da equação (1): \( b = -9 – a \)
🔎 Etapa 3 – Substituir na equação (2):
Substituímos \( b \) em (2):
$$ (-9 – a)^2 – a^2 = 54 $$
Expansão do quadrado:
$$ (81 + 18a + a^2) – a^2 = 54 $$
Eliminando \( a^2 \):
$$ 81 + 18a = 54 $$
$$ 18a = -27 \Rightarrow a = -\dfrac{3}{2} $$
Substituindo em (1):
$$ b = -9 – (-\dfrac{3}{2}) = -9 + \dfrac{3}{2} = -\dfrac{15}{2} $$
🔎 Etapa 4 – Calcular \( a – b \):
$$ a – b = -\dfrac{3}{2} – (-\dfrac{15}{2}) = \dfrac{12}{2} = \boxed{6} $$
✅ Conclusão:
- Valor de \( a \): \( -\dfrac{3}{2} \)
- Valor de \( b \): \( -\dfrac{15}{2} \)
- Resultado final: \( a – b = \boxed{6} \)
Conteúdo: Função afim determinada por tabela – aplicação experimental
(Enem/MEC) Um experimento consiste em colocar certa quantidade de bolas de vidro idênticas em um copo com água e medir o nível da água. A tabela a seguir mostra os dados obtidos: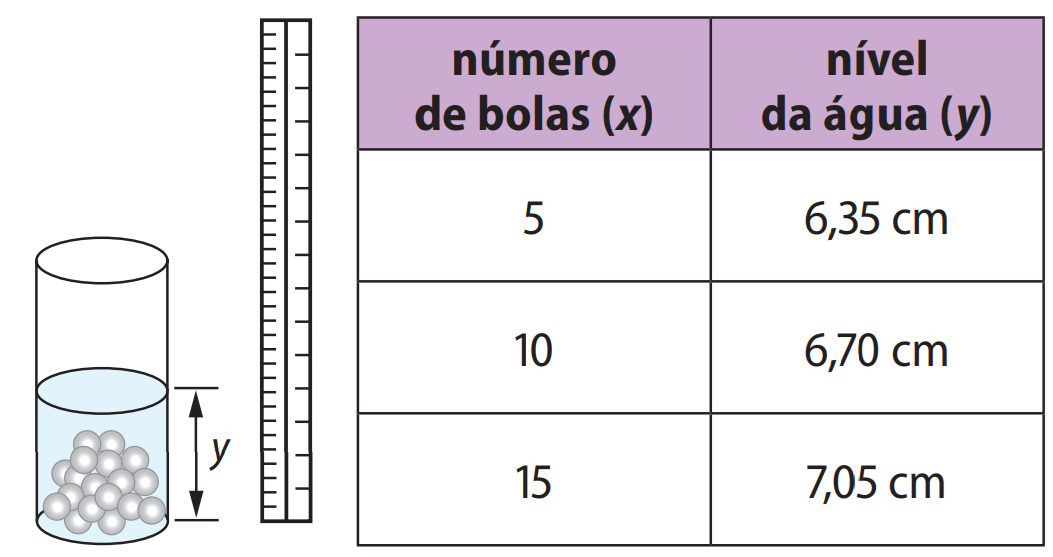
Qual expressão algébrica representa o nível da água \( y \), em função do número de bolas \( x \)?
- a) \( y = 30x \)
- b) \( y = 25x + 20{,}2 \)
- c) \( y = 1{,}2x \)
- d) \( y = 0{,}7x \)
- e) \( y = 0{,}07x + 6 \)
🔍 Ver solução passo a passo
🔎 Etapa 1 – Identificar dois pares ordenados:
- Ponto A: \( (5,\ 6{,}35) \)
- Ponto B: \( (10,\ 6{,}70) \)
🔎 Etapa 2 – Usar a fórmula da função afim:
Seja \( y = ax + b \). Vamos calcular \( a \):
$$ a = \frac{y_2 – y_1}{x_2 – x_1} = \frac{6{,}70 – 6{,}35}{10 – 5} = \frac{0{,}35}{5} = 0{,}07 $$
🔎 Etapa 3 – Substituir em um ponto para encontrar \( b \):
Usando o ponto \( (5,\ 6{,}35) \):
$$ 6{,}35 = 0{,}07 \cdot 5 + b \Rightarrow 6{,}35 = 0{,}35 + b \Rightarrow b = 6 $$
🔎 Etapa 4 – Função final:
$$ y = 0{,}07x + 6 $$
Alternativa correta: e)
✅ Conclusão:
- Coeficiente angular: \( a = 0{,}07 \)
- Coeficiente linear: \( b = 6 \)
- Função: \( y = 0{,}07x + 6 \)
- Alternativa correta: e)























