Função do Segundo Grau ou Quadrática: Um Guia Completo

A função do segundo grau, também conhecida como função quadrática, é um dos conceitos mais fundamentais da matemática. Presente em diversas áreas como física, economia, engenharia e até mesmo em nosso cotidiano, ela desempenha um papel crucial na modelagem de situações em que há uma relação de dependência entre duas variáveis, resultando em uma curva parabólica. Neste artigo, exploraremos em detalhes o que é uma função do segundo grau, sua fórmula geral, suas principais características, e como resolver problemas envolvendo essa função.

O Que é uma Função do Segundo Grau?

Uma função do segundo grau é uma relação matemática expressa pela fórmula:

f(x) = ax² + bx + c

onde:

• a, b e c são coeficientes reais,
• x é a variável independente,
• f(x) é o valor da função para um dado valor de x.

O coeficiente ( a ) é crucial para determinar a forma da parábola, enquanto b e c influenciam a posição da parábola no plano cartesiano.

Características da Função do Segundo Grau

1. Forma da Parábola: A função do segundo grau sempre resulta em um gráfico com a forma de uma parábola. Dependendo do sinal de a, a parábola pode ter uma concavidade voltada para cima se ( a > 0 ) ou para baixo (se a < 0).
2. Vértice: O vértice da parábola é o ponto em que ela atinge seu valor máximo ou mínimo, dependendo do sinal de a. O vértice é dado pelas coordenadas:

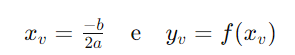
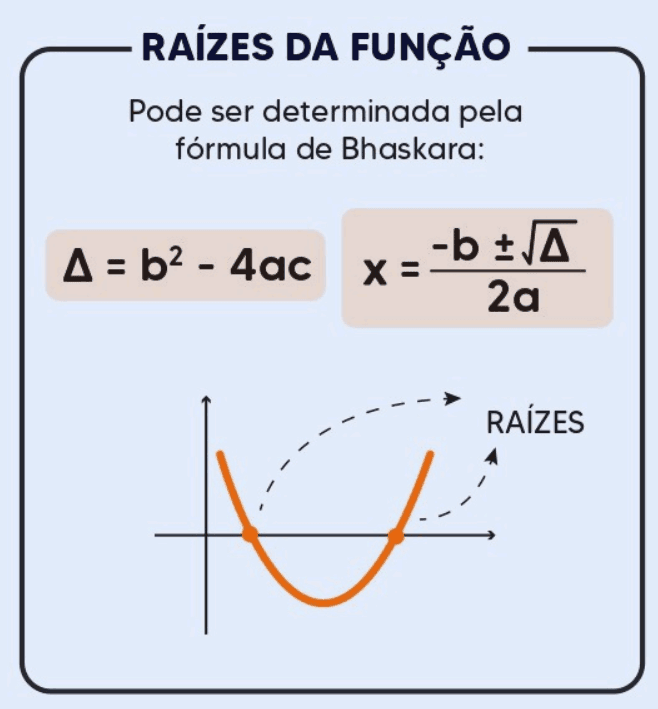
3. Raízes: As raízes da função do segundo grau são os valores de x para os quais f(x) = 0. Elas podem ser encontradas utilizando a fórmula de Bhaskara:

O discriminante ( ∆ = b² – 4ac ) determina a natureza das raízes:

• Se ( ∆ > 0 ), a função tem duas raízes reais e distintas.
• Se ( ∆= 0 ), a função tem uma raiz real dupla (as duas raízes coincidem).
• Se ( ∆ < 0 ), a função não tem raízes reais (as raízes são complexas).

1. Eixo de Simetria: A parábola é simétrica em relação a uma linha vertical que passa pelo vértice, chamada de eixo de simetria. Essa linha tem a equação ( x = x_v ).
2. Interseção com o Eixo y: A função do segundo grau intersecta o eixo y no ponto (0, c).

Leia também: Equação do Segundo grau

Vértice da Função do Segundo Grau

Toda função do segundo grau apresenta uma parábola que pode ter sua concavidade voltada para cima, o que implica em um ponto de mínimo, ou voltada para baixo, resultando em um ponto de máximo. Esse ponto de mínimo ou máximo é conhecido como vértice da parábola.

Seja V o vértice da parábola, com coordenadas (x_v, y_v). As fórmulas para encontrar essas coordenadas são:

Exemplo 1: Considere a função f(x)= 3x² − 6x + 4.

• Primeiro, identificamos os coeficientes: a = 3 , b = −6, c = 4.
• Calculamos x_v​:

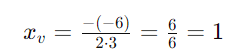
Agora, substituímos x_v=1 na função para encontrar y_v​:

y_v​=3(1)² − 6(1) + 4= 3 − 6 + 4 = 1

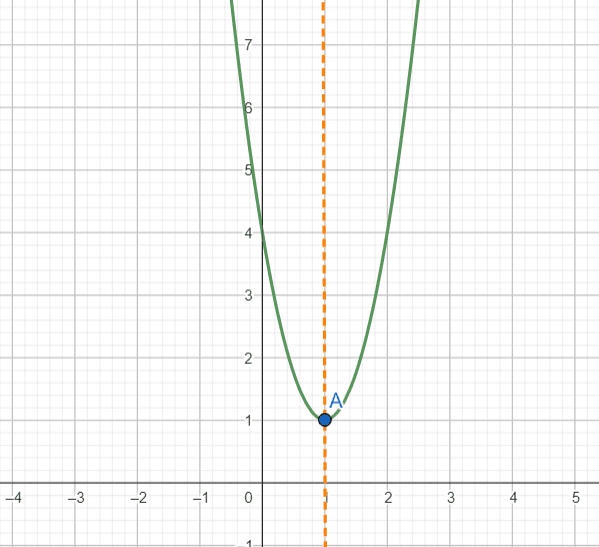
O vértice dessa parábola é V(1, 1).

Observe o eixo de simetria e o vértice na função no gráfico abaixo.

Exemplos de Funções do Segundo Grau

Vamos considerar alguns exemplos de funções do segundo grau para ilustrar esses conceitos.

1. Exemplo 1: Considere a função f(x) = 2x² + 3x – 5.

• Coeficientes: a = 2, b = 3, c = -5.
• Vértice: x_v = -3/2.2 = -3/4 .
• Discriminante: ∆ = 3² – 4.2.(-5) = 9 + 40 = 49.

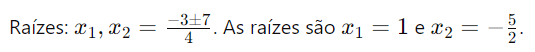
Aplicações da Função do Segundo Grau

As funções do segundo grau são amplamente utilizadas para modelar fenômenos do mundo real. Algumas aplicações incluem:

1. Lançamento de Projéteis: A trajetória de um projétil sob a influência da gravidade, como uma bola arremessada no ar, é descrita por uma parábola. A equação que descreve essa trajetória é uma função do segundo grau.
2. Óptica: Em óptica, as parábolas são usadas para descrever a forma de espelhos parabólicos, que têm a propriedade de refletir a luz em direção a um ponto focal.
3. Economia: As funções do segundo grau também aparecem em economia, como no caso das curvas de lucro, que descrevem a relação entre o lucro e o nível de produção ou investimento.
4. Engenharia: Na engenharia, as funções quadráticas são usadas para modelar uma variedade de sistemas, incluindo o comportamento de estruturas e materiais sob carga.

Resolução de Problemas Envolvendo Funções do Segundo Grau

Resolver problemas que envolvem funções do segundo grau geralmente envolve a identificação dos coeficientes a, b e c, o cálculo do discriminante ∆, e a aplicação da fórmula de Bhaskara para encontrar as raízes. Além disso, a interpretação do gráfico da função pode ajudar a entender melhor o comportamento da função em diferentes contextos.

Exemplo de Problema Resolvido

Problema: Uma empresa fabrica e vende um determinado produto, e o lucro L obtido pela venda de x unidades é dado pela função L(x) = -2x² + 12x – 16. Qual é o número de unidades que a empresa deve vender para maximizar o lucro, e qual é esse lucro máximo?

Solução:

Primeiro, identificamos os coeficientes: a = -2, b = 12, c = -16.

O vértice da parábola, que dá o valor de x que maximiza o lucro, é encontrado por

x_v = -12/2.(-2) = -12/-4 = 3.

Para encontrar o lucro máximo, substituímos x = 3 na função L(x):

L(3) = -2(3)² + 12(3) – 16
L(3) = -18 + 36 – 16 = 2

Portanto, a empresa deve vender 3 unidades para obter um lucro máximo de 2 unidades monetárias.

Análise do Delta (Δ): Discriminante da função do segundo grau

O discriminante Δ, também conhecido como delta, é uma parte fundamental da fórmula de Bhaskara e desempenha um papel crucial na determinação das raízes de uma função do segundo grau. O discriminante é calculado a partir dos coeficientes da função quadrática:

Δ= b₂ – 4ac

onde a, b e c são os coeficientes da função quadrática f(x) = ax² + bx + c. O valor de Δ nos dá informações importantes sobre a natureza das raízes da equação quadrática.

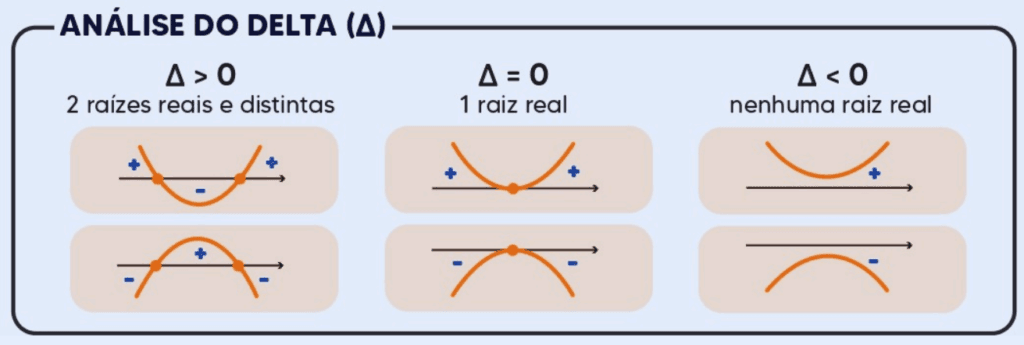
Análise do Delta e Suas Implicações

1. Delta Positivo Δ> 0:

• Natureza das Raízes: Quando Δ é maior que zero, a equação quadrática possui duas raízes reais e distintas. Isso significa que a parábola intercepta o eixo x em dois pontos diferentes.
• Interpretação Gráfica: O gráfico da função mostra uma parábola que cruza o eixo x em dois pontos diferentes. Este cenário ocorre quando o discriminante é positivo e resulta em dois valores distintos de x.
• Exemplo: Para a função f(x) = x² – 5x + 6, temos:
  Δ= (-5)² – 4.1.6 = 25 – 24 = 1
  Δ = 1, a função possui duas raízes reais e distintas.

1. Delta Igual a Zero Δ = 0:

• Natureza das Raízes: Quando Δ é igual a zero, a equação quadrática possui uma única raiz real dupla. Isso significa que a parábola toca o eixo x em exatamente um ponto, e a raiz é chamada de raiz dupla ou repetida.
• Interpretação Gráfica: O gráfico da função mostra uma parábola que é tangente ao eixo x, ou seja, toca o eixo em um único ponto sem cruzá-lo. Exemplo: Para a função f(x) = x² – 4x + 4, temos:
  Δ = (-4)² – 4.1.4 = 16 – 16 = 0
  Como Δ = 0, a função possui uma raiz real dupla.

1. Delta Negativo Δ < 0:

• Natureza das Raízes: Quando Δ é menor que zero, a equação quadrática não possui raízes reais. Em vez disso, as raízes são números complexos conjugados, indicando que a parábola não intercepta o eixo x.
• Interpretação Gráfica: O gráfico da função mostra uma parábola que não cruza o eixo x. Isso acontece porque não há valores de x para os quais f(x) = 0 dentro do conjunto dos números reais.
• Exemplo: Para a função f(x) = x² + 2x + 5, temos:
  Δ = 2² – 4.1.5 = 4 – 20 = -16
  Como Δ = -16, a função não possui raízes reais, apenas raízes complexas.

Importância do Delta

O valor de Δ é fundamental na análise de funções quadráticas, pois determina a natureza das soluções da equação e a forma do gráfico da função. Essa análise é importante em diversas áreas, como na física, onde a solução de uma equação quadrática pode representar o tempo de voo de um projétil, ou na engenharia, onde pode indicar os pontos de tensão máxima em uma estrutura.

A análise do delta é um passo essencial para compreender completamente as raízes de uma função do segundo grau. Com base no valor de Δ, podemos prever se a função terá duas raízes reais e distintas, uma raiz real dupla, ou se as raízes serão complexas. Isso não só ajuda na resolução de equações quadráticas, mas também oferece uma visão mais profunda sobre o comportamento gráfico e a aplicabilidade da função em diferentes contextos.

Representação Gráfica de uma Função do 2º Grau

Para realizar o esboço do gráfico de uma função do 2º grau, é essencial identificar três elementos chave: as raízes ou zeros da função, o vértice, e o ponto de interseção da função com o eixo y. Esses elementos nos fornecem as coordenadas necessárias para desenhar a parábola que representa a função no plano cartesiano. Vamos explorar esse processo passo a passo usando um exemplo prático.

Exemplo:

Considere a função quadrática f(x) = x² – 6x + 8.

1º Passo: Determinar as Raízes da Função

As raízes da função são os pontos onde a parábola intercepta o eixo x, ou seja, os valores de x para os quais f(x) = 0. Esses pontos têm a forma

(x’, 0) e (x”, 0).

Para encontrar as raízes, devemos resolver a equação quadrática:

x² – 6x + 8 = 0

Identificamos os coeficientes:

• a = 1
• b = -6
• c = 8

Agora, aplicamos a fórmula de Bhaskara para encontrar as raízes:

Δ = b^2 – 4ac
Δ = (-6)² – 4.1.8 = 36 – 32 = 4

Com Δ = 4, as raízes podem ser calculadas como:

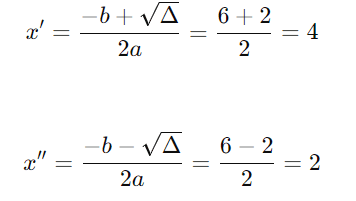
Portanto, as raízes da função são x’ = 4 e x” = 2, correspondendo aos pontos (4, 0) e (2, 0).

2º Passo: Encontrar o Vértice da Parábola

O vértice é o ponto da parábola onde ocorre o valor máximo ou mínimo da função, dependendo da concavidade. As coordenadas do vértice V(x_v, y_v) podem ser encontradas usando as fórmulas:

Para encontrar a coordenada y_v, substituímos x_v = 3 na função original:

y_v = f(3) = (3)² – 6(3) + 8 = 9 – 18 + 8 = -1

Assim, o vértice da parábola é o ponto V(3, -1).

3º Passo: Interseção com o Eixo ( y )

A interseção da parábola com o eixo y ocorre quando x = 0. Para encontrar este ponto, simplesmente avaliamos f(0):

f(0) = (0)² – 6(0) + 8 = 8

Portanto, o ponto de interseção com o eixo y é (0, 8).

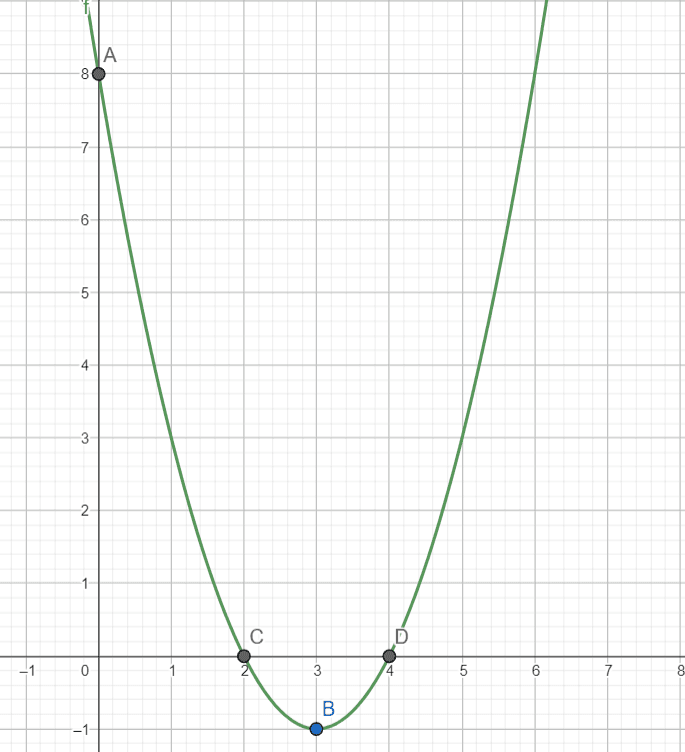
Esboço do Gráfico

Com os elementos que identificamos:

• As raízes são 4 e 2 logo, passando pelos pontos (4, 0) ) e (2, 0),
• O vértice (3, -1),
• E a interseção com o eixo y no ponto (0, 8),

podemos esboçar o gráfico da função f(x) = x² – 6x + 8. A parábola terá uma concavidade voltada para cima, passará pelos pontos (4, 0) e (2, 0), e tocará seu ponto mínimo no vértice (3, -1). O ponto (0, 8) indica onde a parábola cruza o eixo y, proporcionando uma visão clara de como a função se comporta graficamente.

Considerações Finais

As funções do segundo grau são uma ferramenta poderosa na matemática, com aplicações que vão desde a física até a economia. Compreender suas propriedades e aprender a resolvê-las é essencial para quem deseja dominar a matemática em níveis mais avançados. Esperamos que este artigo tenha proporcionado uma visão abrangente sobre o assunto, ajudando tanto aqueles que estão começando a aprender sobre funções quadráticas quanto aqueles que procuram revisar e aprofundar seus conhecimentos.

Se você tem interesse em explorar mais sobre funções matemáticas, não hesite em continuar suas leituras e exercícios. A matemática é uma jornada contínua de aprendizado, e cada conceito dominado abre novas portas para aplicações mais complexas e fascinantes.