Introdução
A porcentagem é uma ferramenta da matemática básica essencial que usamos em diversas situações do cotidiano, seja para calcular descontos, juros, aumentos salariais, ou até mesmo para entender dados estatísticos. Este artigo explora o conceito de porcentagem, apresenta as fórmulas mais utilizadas, e oferece exemplos práticos para ajudar você a dominar o assunto.
O Que é Porcentagem?
Porcentagem é uma forma de expressar uma fração com denominador 100. A palavra “porcentagem” vem do latim “per centum”, que significa “por cento”. Em termos simples, uma porcentagem representa uma parte de um todo dividido em 100 partes iguais. Por exemplo, 25% significa 25 partes de um total de 100.
Fórmula Básica da Porcentagem
A fórmula básica para calcular a porcentagem é:
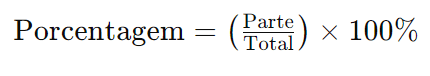
Onde:
- Parte é o valor que você deseja expressar em relação ao total.
- Total é o valor total de referência.
Exemplo 1: Calcular a Porcentagem de um Valor
Imagine que você tem um caderno com 200 páginas e já leu 50 páginas. Qual a porcentagem do caderno que você já leu?
Vamos aplicar a fórmula:

Conclusão: Você já leu 25% do caderno.
Exemplo 2: Calcular um Valor a partir de uma Porcentagem
Agora, suponha que em uma loja, um produto que custa R$ 150,00 está com 20% de desconto. Quanto será descontado e qual o preço final do produto?
Primeiro, calcule o valor do desconto:
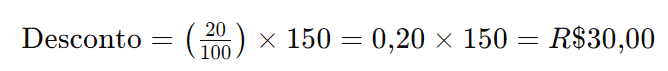
Agora, subtraia o desconto do preço original para encontrar o preço final:
Preço Final = 150 – 30 = R$ 120,00
Conclusão: O produto custará R$ 120,00 após o desconto.
Lista de Exercício Porcentagem
Aumento ou Redução Percentual
Outra aplicação comum da porcentagem é o cálculo de aumentos ou reduções percentuais. Quando um valor é aumentado ou reduzido por uma certa porcentagem, utilizamos a fórmula:
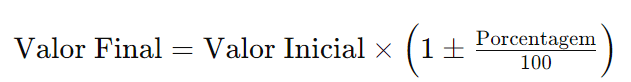
O sinal “+” é usado para aumentos, enquanto o sinal “–” é usado para reduções.
Exemplo 3: Calcular um Aumento Percentual
Você recebeu um aumento salarial de 10%, e seu salário inicial era de R$ 2.500,00. Qual será o seu novo salário?
Aplicando a fórmula:
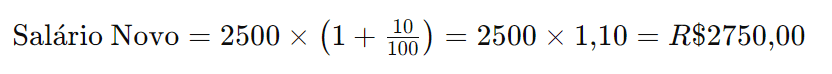
Conclusão: Após o aumento, seu novo salário será R$ 2.750,00.
Exemplo 4: Calcular uma Redução Percentual
Imagine que o preço de uma mercadoria foi reduzido em 15%, e o preço original era R$ 80,00. Qual é o novo preço?
Aplicando a fórmula:

Conclusão: O novo preço da mercadoria será R$ 68,00.
Porcentagem Acumulada
Porcentagem acumulada refere-se ao efeito de múltiplos aumentos ou reduções percentuais aplicados em sequência. Para calcular, multiplicamos os fatores de aumento ou redução.
Exemplo 5: Porcentagem Acumulada em Dois Aumentos
Suponha que um produto teve um aumento de 20% e, em seguida, mais 10%. Se o preço original era R$ 100,00, qual é o preço final após os dois aumentos?
Primeiro, aplique o primeiro aumento:
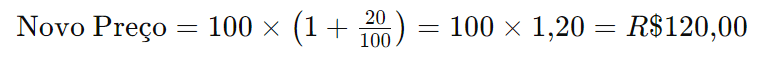
Agora, aplique o segundo aumento ao novo preço:
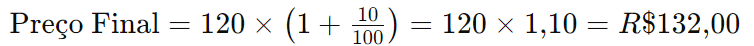
Conclusão: O preço final do produto será R$ 132,00 após os dois aumentos.
Aumento Sucessivo
O aumento sucessivo ocorre quando aplicamos uma série de aumentos percentuais sobre um valor inicial, um após o outro. Cada aumento é calculado sobre o valor resultante do aumento anterior.
Fórmula:
Para dois aumentos sucessivos de a% e b% sobre um valor inicial ( Vi ), o valor final ( Vf ) é:
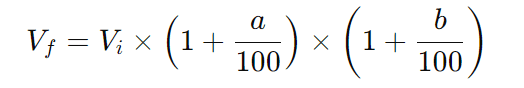
Exemplo:
Um produto custa R$ 100,00 e recebe aumentos de 10% e 20%. O valor final será:
- Primeiro aumento: 100 x 1,10 = R$ 110,00
- Segundo aumento: 110 x 1,20 = R$ 132,00
Resultado: O produto custará R$ 132,00 após os aumentos.
Desconto Sucessivo
O desconto sucessivo funciona de maneira similar, mas em vez de aumentar, reduz o valor inicial. Cada desconto é aplicado sobre o valor resultante do desconto anterior.
Fórmula:
Para dois descontos sucessivos de a% e b%, o valor final ( Vf ) é:
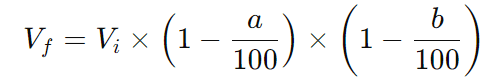
Exemplo:
Um produto custa R$ 100,00 e recebe descontos de 10% e 20%. O valor final será:
- Primeiro desconto: 100 x 0,90 = R$ 90,00
Resultado: O produto custará R$ 72,00 após os descontos.
Resumo:
- Aumento Sucessivo: Aumenta o valor, aplicando cada aumento sobre o resultado anterior.
- Desconto Sucessivo: Reduz o valor, aplicando cada desconto sobre o resultado anterior.
Aumento e Desconto Simultâneos
Quando um valor é submetido a um aumento e, em seguida, a um desconto (ou vice-versa), o cálculo não é simplesmente a soma ou subtração direta das porcentagens. Cada operação é aplicada sucessivamente sobre o valor resultante da operação anterior.
Fórmula Geral
Para um valor inicial Vi, com um aumento de a% seguido por um desconto de b% (ou na ordem inversa), o valor final Vf é calculado como:
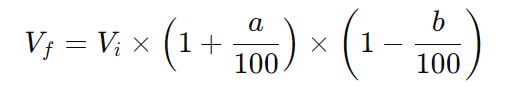
Exemplo 1: Aumento Seguido de Desconto
Suponha que um produto custa R$ 200,00. Ele recebe primeiro um aumento de 15% e depois um desconto de 10%. O cálculo seria:
- Aumento de 15%: V1 = 200 × 1,15 = R$230,00
- Desconto de 10% sobre o Novo Valor: Vf = 230 × 0,90 = R$207,00
Resultado: Após o aumento e o desconto, o valor final será R$ 207,00.
Exemplo 2: Desconto Seguido de Aumento
Agora, considere o mesmo produto de R$ 200,00, mas desta vez aplicamos primeiro um desconto de 10% e depois um aumento de 15%. O cálculo seria:
- Desconto de 10%: V1 = 200 × 0,90 = R$180,00
- Aumento de 15% sobre o Novo Valor: Vf = 180 × 1,15 = R$207,00
Resultado: Neste caso, o valor final também será R$ 207,00.
Conclusão
Entender o conceito de porcentagem e saber aplicá-lo é fundamental para diversas áreas da vida cotidiana e profissional. Desde calcular descontos em compras até determinar aumentos salariais, a porcentagem é uma ferramenta poderosa e versátil. Esperamos que os exemplos resolvidos neste artigo tenham facilitado sua compreensão e que você se sinta mais confiante ao lidar com cálculos percentuais no futuro.
Se você ainda tiver dúvidas ou desejar aprender mais, continue praticando com diferentes tipos de problemas, pois a prática é a chave para a maestria em matemática!
Lista de Exercícios sobre Porcentagem, Aumento, e Desconto
Exercício 1
Um produto custa R$ 150,00. Se ele sofrer um aumento de 10%, qual será o novo preço?
a) R$ 155,00
b) R$ 160,00
c) R$ 165,00
d) R$ 150,00
Exercício 2
Um celular estava sendo vendido por R$ 1.200,00 e sofreu um desconto de 15%. Qual o preço após o desconto?
a) R$ 1.020,00
b) R$ 1.100,00
c) R$ 1.180,00
d) R$ 1.140,00
Exercício 3
Se um valor de R$ 500,00 recebe dois aumentos sucessivos de 10% e 5%, qual será o valor final?
a) R$ 577,50
b) R$ 550,00
c) R$ 555,00
d) R$ 562,50
Exercício 4
Um desconto sucessivo de 20% e 10% foi aplicado a um produto que custa R$ 250,00. Qual é o preço final?
a) R$ 175,00
b) R$ 180,00
c) R$ 200,00
d) R$ 225,00
Exercício 5
Se um produto que custa R$ 80,00 tem um desconto de 20% e, em seguida, um aumento de 25%, qual será o preço final?
a) R$ 75,00
b) R$ 80,00
c) R$ 85,00
d) R$ 90,00
Exercício 6
O preço de uma televisão aumentou 20% e agora custa R$ 1.800,00. Qual era o preço original?
a) R$ 1.500,00
b) R$ 1.550,00
c) R$ 1.600,00
d) R$ 1.650,00
Exercício 7
Um salário de R$ 2.000,00 teve um aumento de 12%. Qual é o novo salário?
a) R$ 2.120,00
b) R$ 2.220,00
c) R$ 2.240,00
d) R$ 2.250,00
Exercício 8
Um produto de R$ 200,00 recebeu um desconto de 25%. Quanto foi descontado?
a) R$ 40,00
b) R$ 50,00
c) R$ 60,00
d) R$ 70,00
Exercício 9
Se um bem que custa R$ 1.000,00 tem seu preço aumentado em 15% e depois sofre um desconto de 10%, qual será o preço final?
a) R$ 1.045,00
b) R$ 1.050,00
c) R$ 1.055,00
d) R$ 1.060,00
Exercício 10
Uma loja oferece um desconto de 20% em um produto que custa R$ 500,00 e, depois, aplica um aumento de 10% sobre o novo preço. Qual é o valor final do produto?
a) R$ 432,00
b) R$ 435,00
c) R$ 440,00
d) R$ 450,00
Exercício 11
Um computador custa R$ 2.500,00 e foi oferecido um desconto de 12%. Qual é o preço do computador com o desconto?
a) R$ 2.200,00
b) R$ 2.250,00
c) R$ 2.300,00
d) R$ 2.350,00
Exercício 12
O preço de um item foi reduzido de R$ 400,00 para R$ 320,00. Qual foi o percentual de desconto?
a) 15%
b) 20%
c) 25%
d) 30%
Exercício 13
Uma ação valorizou-se em 25% em um mês e, no mês seguinte, desvalorizou-se em 20%. Se o preço inicial da ação era R$ 100,00, qual é o preço após os dois meses?
a) R$ 100,00
b) R$ 102,00
c) R$ 105,00
d) R$ 108,00
Exercício 14
Um produto foi vendido com um aumento de 15% e, posteriormente, foi dado um desconto de 10%. Se o preço inicial era R$ 300,00, qual foi o preço final?
a) R$ 297,00
b) R$ 305,00
c) R$ 310,50
d) R$ 315,00
Exercício 15
Um produto custa R$ 80,00. Se ele sofrer um aumento de 15% e depois um desconto de 10%, qual será o valor final?
a) R$ 82,80
b) R$ 84,00
c) R$ 86,40
d) R$ 88,00
Exercício 16
Se um produto de R$ 150,00 recebeu um desconto de 30% e depois um aumento de 20%, qual é o preço final?
a) R$ 120,00
b) R$ 126,00
c) R$ 132,00
d) R$ 135,00
Exercício 17
Um imóvel teve seu valor aumentado em 10% e, logo depois, foi aplicado um desconto de 15%. Se o valor inicial do imóvel era R$ 200.000,00, qual será o valor final?
a) R$ 186.000,00
b) R$ 190.000,00
c) R$ 195.500,00
d) R$ 198.000,00
Exercício 18
Uma loja aplica um desconto de 25% em um produto que custa R$ 400,00. Em seguida, aumenta o preço em 10%. Qual é o valor final do produto?
a) R$ 315,00
b) R$ 320,00
c) R$ 325,00
d) R$ 330,00
Exercício 19
Um veículo foi anunciado com um preço de R$ 50.000,00. Após um aumento de 8% e um desconto de 5%, qual é o preço final do veículo?
a) R$ 51.800,00
b) R$ 52.000,00
c) R$ 52.300,00
d) R$ 52.500,00
Exercício 20
Se um produto custa R$ 1.000,00 e recebeu dois descontos sucessivos de 15% e 10%, qual será o preço final?
a) R$ 765,00
b) R$ 765,50
c) R$ 770,00
d) R$ 775,00
Gabarito
- c) R$ 165,00
- a) R$ 1.020,00
- d) R$ 562,50
- b) R$ 180,00
- c) R$ 85,00
- c) R$ 1.500,00
- c) R$ 2.240,00
- c) R$ 50,00
- a) R$ 1.045,00
- d) R$ 450,00
- c) R$ 2.200,00
- b) 20%
- b) R$ 102,00
- a) R$ 297,00
- a) R$ 82,80
- b) R$ 126,00
- a) R$ 186.000,00
- c) R$ 325,00
- d) R$ 52.300,00
- b) R$ 765,50