O que é uma inequação do segundo grau?
Uma inequação do segundo grau na matemática tem a seguinte forma geral:
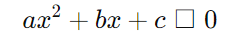
Onde:
- ( a ), ( b ) e ( c ) são coeficientes reais com ( a ≠ 0 );
- O símbolo ( ▢) pode ser (maior que), < (menor que), ≥ (maior ou igual a), ≤ (menor ou igual a).
O objetivo é encontrar os valores de ( x ) que tornam a inequação verdadeira. Para isso, é necessário analisar o sinal da função quadrática ( ax2 + bx + c ), que é um polinômio de segundo grau.
Passos para resolver uma inequação do segundo grau
Igualar a inequação a zero: A primeira etapa é transformar a inequação em uma equação quadrática. Exemplo:
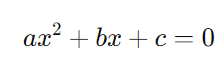
Calcular o discriminante (Δ): Utilizando a fórmula do discriminante ( Δ = b2 – 4ac ), determinamos as raízes da equação associada.
Encontrar as raízes da equação quadrática: Com o discriminante, utilizamos a fórmula de Bhaskara para encontrar as soluções da equação:
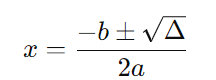
Analisar o sinal da função quadrática: Dependendo do valor de ( Δ ) e do sinal de ( a ), o gráfico da função ( f(x) = ax2 + bx + c ) será uma parábola voltada para cima ( a > 0 ) ou para baixo ( a < 0 ). Isso ajuda a definir os intervalos em que a função é positiva ou negativa.
Resolver a inequação: Com as raízes da equação e a análise do sinal, determinamos os intervalos em que a inequação é verdadeira.
Exemplos Resolvidos
Exemplo 1: Resolva a inequação ( x2 – 3x + 2 > 0 ).
Passo 1: Igualar a inequação a zero:
x2 – 3x + 2 = 0
Passo 2: Calcular o discriminante:
Δ = (-3)2 – 4(1)(2) = 9 – 8 = 1
Passo 3: Encontrar as raízes da equação:
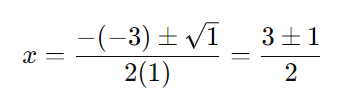
Portanto, as raízes são:
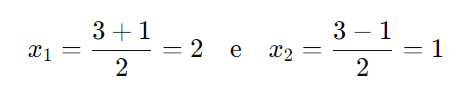
Passo 4: Analisar o sinal da função quadrática:
Como ( a = 1 > 0 ), a parábola é voltada para cima. As raízes são ( x1 = 2 ) e ( x2 = 1 ). Portanto, o gráfico da função é negativo entre as raízes e positivo fora delas. Assim, a inequação ( x2 – 3x + 2 > 0 ) é satisfeita nos intervalos (−∞,1) ∪ (2,+∞).

Resposta: (−∞,1) ∪ (2,+∞).
Exemplo 2: Resolva a inequação ( 2x2 – 5x ≤ 3 ).
Passo 1: Colocar a inequação na forma padrão:
2x2 – 5x – 3 ≤ 0
Passo 2: Calcular o discriminante:
= (-5)2 – 4(2)(-3) = 25 + 24 = 49
Passo 3: Encontrar as raízes da equação:
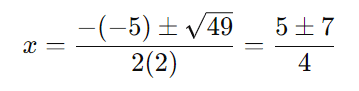
As raízes são:
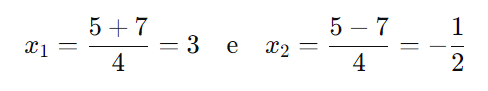
Passo 4: Analisar o sinal da função quadrática:
Como ( a = 2 > 0 ), a parábola é voltada para cima. A função ( 2x2 – 5x – 3 ) é negativa entre as raízes ( x2 = -1/2) e ( x1 = 3 ), e positiva fora desse intervalo.
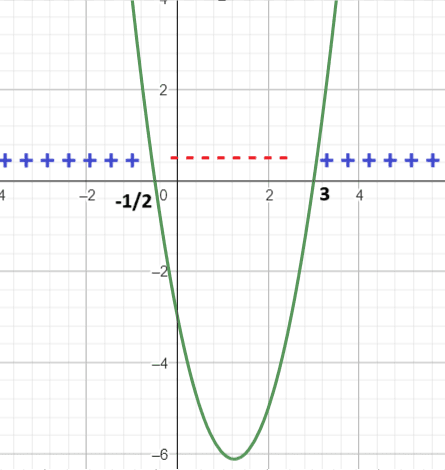
Passo 5: Resolver a inequação ( 2x2 – 5x – 3 ≤ 0 ):
A inequação é satisfeita no intervalo fechado entre as raízes, ou seja:
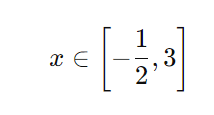
Resposta: x ∈ [−1/2,3]
.
Exemplo 3: Resolva a inequação ( -x2 + 4x – 3 < 0 ).
Passo 1: Igualar a inequação a zero:
-x2 + 4x – 3 = 0
Passo 2: Calcular o discriminante:
Δ = (4)2 – 4(-1)(-3) = 16 – 12 = 4
Passo 3: Encontrar as raízes da equação:
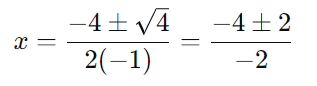
As raízes são:
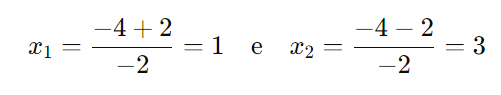
Passo 4: Analisar o sinal da função quadrática:
Como ( a = -1 < 0 ), a parábola é voltada para baixo. Portanto, a função ( -x2 + 4x – 3 ) é negativa fora das raízes e positiva entre as raízes.
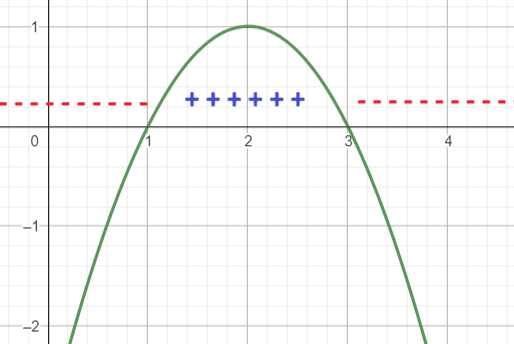
Passo 5: Resolver a inequação ( -x2 + 4x – 3 < 0 ):
A inequação é satisfeita nos intervalos fora das raízes, ou seja:
x∈(−∞,1) ∪ (3,+∞)
Resposta: x∈(−∞,1) ∪ (3,+∞).
Conclusão
As inequações do segundo grau podem ser resolvidas por meio de uma análise cuidadosa do discriminante e das raízes da equação associada. É importante observar o comportamento da função quadrática (se a parábola está voltada para cima ou para baixo) para determinar corretamente os intervalos onde a inequação é satisfeita. A prática com diferentes tipos de inequações ajuda a solidificar a compreensão dos conceitos e técnicas envolvidas.













