(CESPE / CEBRASPE 2024 – Prefeitura de Camaçari – BA – Assistente Administrativo)
Uma empresa verificou que só haverá lucro na venda de 100 unidades de determinado produto se o seu preço p satisfizer à desigualdade -10p2 + 480p – 4.320 > 0. Nesse caso, para que a empresa registre lucro na venda do produto, é necessário que
A) R$ 12,00 < p < R$ 36,00.
B) p = R$ 1.440,00.
C) p > 0.
D) p > R$ 36,00.
E) 0 < p < R$ 12,00.
Vamos resolver a desigualdade dada para encontrar o intervalo de preços ( p ) em que a empresa terá lucro.
Passo a Passo:
- Análise da desigualdade: A desigualdade dada é: [
-10p2 + 480p – 4320 > 0
Essa é uma inequação do segundo grau da forma ( ax2 + bx + c > 0 ), onde:
- ( a = -10 )
- ( b = 480 )
- ( c = -4320 )
Verifique a alternativa correta: A empresa terá lucro na venda do produto se o preço ( p ) estiver no intervalo: A) R$ 12,00 < p < R$ 36,00.
Calcule as raízes da equação quadrática associada: Para resolver a inequação, precisamos encontrar as raízes da equação quadrática correspondente:
-10p2 + 480p – 4320 = 0
Podemos usar a fórmula de Bhaskara:
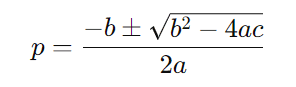
Substituindo os valores de ( a ), ( b ), e ( c ):
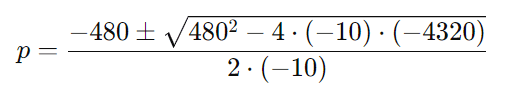
Calcule o discriminante (Δ):

Agora, calcule as raízes:

Então, temos duas raízes:
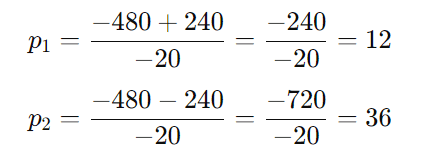
Determine o intervalo da solução: As raízes da equação são ( p1 = 12 ) e ( p2 = 36 ). Como o coeficiente de ( p2 ) é negativo (-10), a parábola abre para baixo. Assim, a desigualdade ( -10p2 + 480p – 4320 > 0 é satisfeita entre as raízes. Portanto, a solução é o intervalo:
12 < p < 36
Verifique a alternativa correta:
A empresa terá lucro na venda do produto se o preço ppp estiver no intervalo:
A) R$ 12,00 < p < R$ 36,00.
Outra maneira de resolver:
Vamos dividir a inequação dada por 10 para simplificar e resolver o problema.
Passo a Passo:
Divida a inequação por 10: A inequação original é:
-10p2 + 480p – 4320 > 0
Dividindo todos os termos por 10:
-p2 + 48p – 432 > 0
Multiplique por -1 para inverter a desigualdade: Para facilitar, multiplique toda a inequação por -1. Lembre-se de inverter o sinal da desigualdade:
p2 – 48p + 432 < 0
Calcule as raízes da equação quadrática associada: Agora, vamos encontrar as raízes da equação quadrática:
p2 – 48p + 432 = 0
Para isso, usamos a fórmula de Bhaskara:
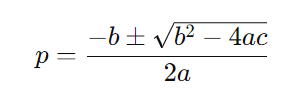
Aqui, (a = 1), (b = -48), e (c = 432). Vamos calcular o discriminante (Δ):

Calcule as raízes:

Determine o intervalo da solução: As raízes da equação são (p1 = 12) e (p2 = 36). Como o coeficiente de (p2) é positivo (1), a parábola abre para cima. A desigualdade (p2 – 48p + 432 < 0) é satisfeita entre as raízes. Portanto, a solução da inequação é o intervalo:
12 < p < 36
Verifique a alternativa correta: A empresa terá lucro na venda do produto se o preço (p) estiver no intervalo: A) R$ 12,00 < p < R$ 36,00.













