Inequação do Segundo Grau – Correios CONSULPLAN – Concurso Público

Vamos resolver essa questão para encontrar o valor de m de modo que o trinômio (m – 2)x² – (m – 1)x + (m – 1) seja sempre positivo utilizando os conhecimentos das inequações do 2° grau.

Para que um trinômio quadrático ( ax² + bx + c ) seja sempre positivo, é necessário que:

1. O coeficiente de ( x² ) seja positivo, ou seja, ( a > 0 ).
2. O discriminante ( ∆ ) da equação quadrática seja negativo, ou seja, ( ∆ < 0 ), para que não haja raízes reais.

Passo 1: Identificar os coeficientes do trinômio

Comparando (m – 2)x² – (m – 1)x + (m – 1) com a equação geral ( ax² + bx + c ), temos:

• a = m – 2
• b = -(m – 1)
• c = m – 1

Passo 2: Garantir que ( a > 0 )

Para que o trinômio seja sempre positivo, o coeficiente de ( ^x2 ), que é ( m – 2 ), deve ser positivo:

m – 2 > 0

m > 2

Passo 3: Calcular o discriminante e garantir que ( ∆ < 0 )

O discriminante ( \Delta ) da equação quadrática é dado por:

∆ = b^2 – 4ac

Substituindo os valores de ( a ), ( b ), e ( c ):

∆ = (-(m – 1))² – 4(m – 2)(m – 1)

Calculando:

∆ = (m – 1)² – 4(m – 2)(m – 1)

Expandindo os termos:

∆ = (m² – 2m + 1) – 4(m² – 3m + 2)

∆ = m² – 2m + 1 – 4(m²) + 12m – 8

∆ = m² – 2m + 1 – 4m² + 12m – 8

Simplificando:

∆ = -3m² + 10m – 7

Para que não haja raízes reais, é necessário que ( ∆ < 0 ):

-3m² + 10m – 7 < 0

Multiplicando a equação por ( -1 ) (lembrando que isso inverte o sinal da desigualdade):

3m² – 10m + 7 > 0

Agora, precisamos resolver a equação quadrática ( 3m² – 10m + 7 = 0 ) para encontrar as raízes.

Passo 4: Encontrar as raízes da equação

Usamos a fórmula de Bhaskara:

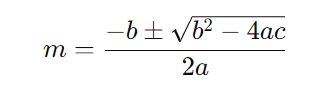
Com ( a = 3 ), ( b = -10 ), e ( c = 7 ):

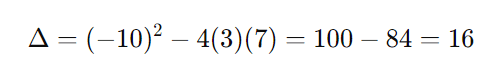
As raízes são:

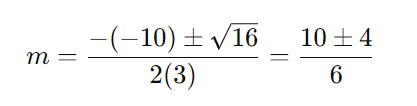
As duas soluções são:

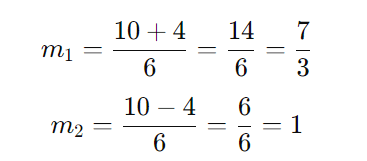
Passo 5: Analisar o sinal da equação

A inequação ( 3m² – 10m + 7 > 0 ) é satisfeita para valores de ( m ) fora do intervalo entre as raízes ( 7/3) e ( 1 ). Portanto, a solução é:

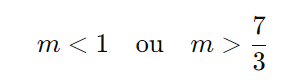
Passo 6: Verificar as opções

A alternativa correta que garante que o trinômio seja sempre positivo é m > 7/3.

A resposta correta é E) m > 2(1/3).