A Lei Binomial da Probabilidade é aplicada em experimentos chamados de Ensaios de Bernoulli, onde há uma sequência de tentativas independentes com dois possíveis resultados: sucesso (S) e fracasso (F). Essa lei permite calcular a probabilidade de ocorrência de um número específico de sucessos em várias tentativas.
Ensaios de Bernoulli
Um ensaio de Bernoulli possui as seguintes características:
- Apenas dois resultados possíveis: sucesso (S) ou fracasso (F).
- A probabilidade de sucesso (p) é constante em todos os ensaios.
- A probabilidade de fracasso é q = 1 – p.
- Os ensaios são independentes, ou seja, o resultado de um ensaio não afeta os outros.
Fórmula da Probabilidade Binomial
Seja n o número total de ensaios e K o número de sucessos desejados. A probabilidade de exatamente K sucessos é dada por:
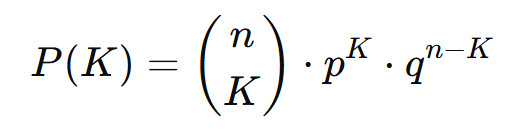
Onde:
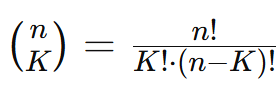
- Número de combinações de n elementos tomados KK a KK.
- p: Probabilidade de sucesso.
- q: Probabilidade de fracasso (q = 1 – p).
- n: Número total de ensaios.
- K: Número de sucessos desejados.
Exemplo 1: Extração de Bolas em uma Urna
Problema:
Uma urna contém 4 bolas vermelhas e 6 bolas brancas. Uma bola é extraída, observada e devolvida à urna. O experimento é repetido 5 vezes. Qual é a probabilidade de observar exatamente 3 bolas vermelhas?
Solução:
Definir os parâmetros:
- Sucesso: Extrair uma bola vermelha (p= 4/10 = 0,4).
- Fracasso: Extrair uma bola branca (q = 6/10 = 0,6).
- Número de ensaios (n = 5).
- Número de sucessos desejados (K = 3).
Cálculo:
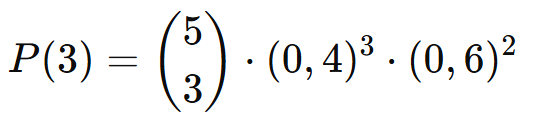
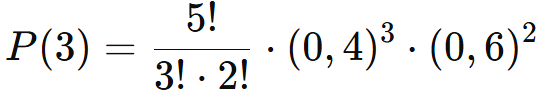
P(3) = 10⋅(0,064)⋅(0,36) = 10⋅0,02304 = 0,2304
Interpretação:
A probabilidade de extrair exatamente 3 bolas vermelhas em 5 ensaios é 23,04%.
Exemplo 2: Pessoas com Carro de Marca A
Problema:
Em uma cidade, 10% das pessoas possuem um carro da marca A. Se 30 pessoas são selecionadas ao acaso, qual é a probabilidade de exatamente 5 delas terem um carro da marca A?
Solução:
Definir os parâmetros:
- Sucesso: Pessoa tem carro da marca A (p = 0,1).
- Fracasso: Pessoa não tem carro da marca A (q = 1 – 0,1 = 0,9).
- Número de ensaios (n = 30).
- Número de sucessos desejados (K = 5).
Cálculo:
Usando aproximações:
P(5) ≈ 142506⋅0,00001⋅0,072 ≈ 0,102
Interpretação:
A probabilidade de que exatamente 5 pessoas tenham carros da marca A é 10,2%.
Distribuição Binomial
Os exemplos acima seguem a distribuição binomial, que descreve a probabilidade de KK sucessos em nn ensaios de Bernoulli. A fórmula geral é:
Essa distribuição é amplamente utilizada em situações práticas, como:
- Lançamento de moedas.
- Lançamento de dados.
- Pesquisas com respostas “sim” ou “não”.
Resumo das Características
- Ensaios independentes: O resultado de um ensaio não interfere nos demais.
- Dois resultados possíveis: Sucesso (S) ou fracasso (F).
- Probabilidades constantes: p e q = 1 – p.
- Fórmula do termo binomial: A probabilidade depende do número de combinações, n, K, p, e q.
Conclusão
A Lei Binomial da Probabilidade é uma ferramenta essencial para calcular probabilidades em experimentos que seguem os princípios dos ensaios de Bernoulli. Com a fórmula binomial, é possível determinar com precisão a probabilidade de obter um número específico de sucessos em situações práticas, tornando-a uma das ferramentas mais úteis na probabilidade.
