As razões trigonométricas são fundamentais para o estudo dos triângulos retângulos e têm ampla aplicação em diversas áreas da matemática e física. Neste artigo, exploramos as três principais razões trigonométricas — seno, cosseno e tangente — que relacionam os ângulos de um triângulo retângulo com seus lados. Cada conceito é acompanhado por uma lista de exercícios resolvidos, garantindo que você compreenda como aplicar essas relações em diferentes situações.
Os exercícios propostos cobrem desde cálculos simples até problemas mais complexos, com foco na identificação e resolução de ângulos e lados desconhecidos em triângulos retângulos. Você encontrará explicações detalhadas que o guiarão em cada etapa, reforçando sua compreensão e habilidade em trigonometria.
Exercícios 01 – Um avião está a 7000 m de altura e inicia a aterrissagem, em aeroporto ao nível do mar. O ângulo de descida é 6º. A que distância da pista está o avião? Qual é a distância que o avião vai percorrer? Dados: sen 6º = 0,10459, cos 6º = 0.99452 e tg 6º = 0,10510
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
Essa questão envolve o uso de trigonometria para determinar duas distâncias: a distância horizontal da pista (que pode ser chamada de d) e a distância total percorrida pelo avião ao descer (que pode ser chamada de s).
1. Cálculo da distância horizontal ( d ) da pista:
O avião forma um triângulo retângulo com a altura h = 7000m e o ângulo de descida θ=6∘. Nesse triângulo, podemos usar a tangente, pois a tangente é a razão entre o cateto oposto (altura) e o cateto adjacente (distância da pista):
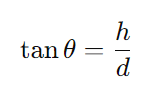
Substituindo os valores:
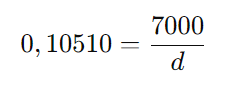
Agora, isolando ( d ):
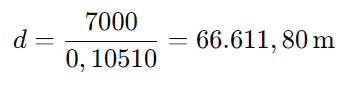
Portanto, a distância horizontal da pista é de aproximadamente 66.611,80 metros.
2. Cálculo da distância total ( s ) que o avião vai percorrer:
A distância total percorrida pelo avião é a hipotenusa do triângulo retângulo. Podemos usar o seno do ângulo de descida, que é a razão entre a altura e a hipotenusa:
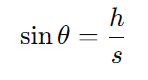
Substituindo os valores:
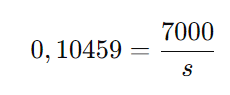
Agora, isolando ( s ):
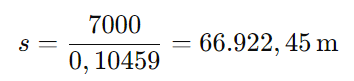
Portanto, a distância total que o avião vai percorrer é de aproximadamente 66.922,45 metros.
Resumo:
- A distância horizontal até a pista é 66.611,80 metros.
- A distância total percorrida pelo avião é 66.922,45 metros.
[/toggle]
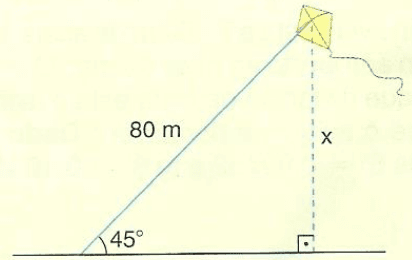
Exercícios 02 – Uma pipa é presa a um fio esticado que forma um ângulo de 45º com o solo. O comprimento do fio é 80 m. determine a altura da pipa em relação ao solo. Dado
√2= 1,41
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
Para resolver este problema, podemos usar trigonometria, já que temos um triângulo retângulo.
Sabemos que:
- O comprimento do fio (hipotenusa) é 80 metros.
- O ângulo formado com o solo é 45°.
- Queremos encontrar a altura (x) da pipa em relação ao solo.
Em um triângulo retângulo com um ângulo de 45°, as duas pernas são iguais, o que significa que a altura (x) é igual à base (x). Podemos usar a função seno ou cosseno de 45° para calcular a altura:
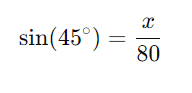
Sabemos que:
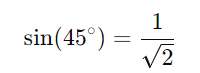
Então, temos a equação:
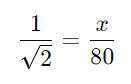
Multiplicando ambos os lados por 80:
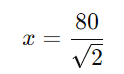
Agora, racionalizando o denominador (multiplicando o numerador e o denominador por √2:
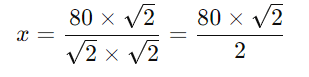
Agora vamos calcular o valor de (x).
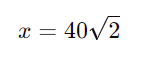
x = 40 x 1,41 = 65,74
A altura da pipa em relação ao solo é aproximadamente 56,74 metros.
[/toggle]
Exercícios 03 – Um barco atravessa um rio, num trecho onde a largura é 100 m, seguindo uma direção que forma 45º com uma das margens. Calcule a distância percorrida pelo
barco para atravessar o rio. Dado √2 = 1,41

[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
Nesse caso, como estamos lidando com a largura do rio (cateto oposto) e queremos calcular a distância percorrida pelo barco (hipotenusa), o correto seria usar a função seno. Vamos refazer o raciocínio utilizando o seno de 45°.
Sabemos que:

Como sin(45∘)=1/√2, a equação se torna:
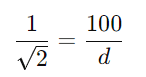
Multiplicando ambos os lados por d e depois por √2:
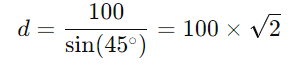
Agora, substituímos o valor de √2=1,41, e o resultado será o mesmo, pois a relação trigonométrica leva ao mesmo valor de hipotenusa. Ou seja:
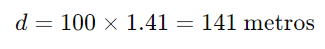
Assim, a distância percorrida pelo barco continua sendo 141 metros.
[/toggle]
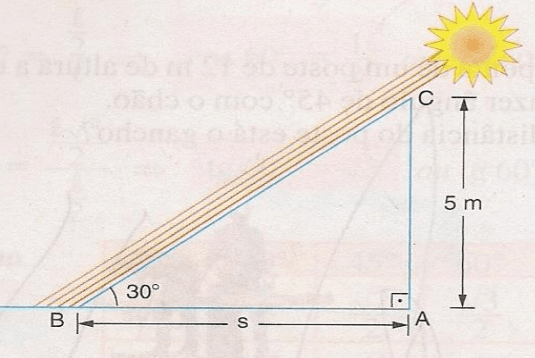
Exercícios 04 – Qual é o comprimento da sombra de uma árvore de 5 m de altura quando o sol está 30º acima do horizonte? Dado √3 = 1,73
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
Neste problema, temos uma árvore de 5 metros de altura e o ângulo de elevação do sol é 30°. Precisamos calcular o comprimento da sombra (s), que é o cateto adjacente em relação ao ângulo de 30° no triângulo retângulo formado.
Usaremos a função tangente, que é a razão entre o cateto oposto (altura da árvore) e o cateto adjacente (comprimento da sombra):

Sabemos que:
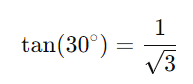
Agora, substituímos os valores:
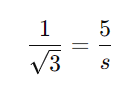
Multiplicando ambos os lados por (s) e depois por √3:
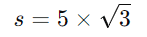
Agora, substituímos o valor de √3 = 1,73 para encontrar o comprimento da sombra:
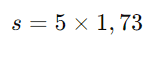
Vamos calcular.
O comprimento da sombra da árvore é aproximadamente 8,65 metros.
[/toggle]
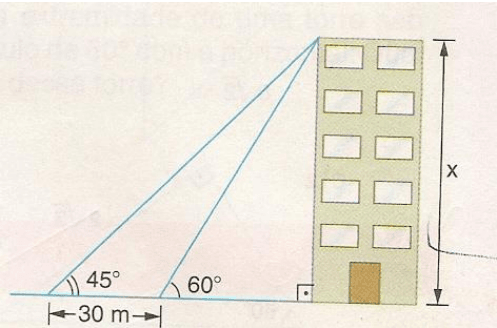
Exercícios 05 – Um observador vê um edifício, construído em terreno plano, sob um ângulo de 60º. Se ele se afastar do edifício mais 30 m, passará a vê – lo sob ângulo de 45º. Calcule a altura do edifício.
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
Vamos resolver o problema passo a passo usando as relações trigonométricas para obter a altura do edifício (x).
Passo 1: Definir as equações trigonométricas
Com base na imagem e nos dados fornecidos, podemos usar as tangentes dos ângulos para definir as relações trigonométricas:
Para o primeiro triângulo com ângulo de 60°:
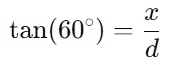
onde (x) é a altura do edifício e (d) é a distância inicial do observador ao prédio. Sabemos que tan(60°) = √3, então temos:
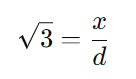
ou
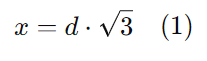
Para o segundo triângulo com ângulo de (45°):
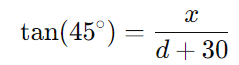
Como tan(45°) = 1, temos:
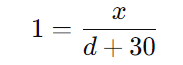
ou
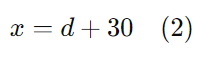
Passo 2: Igualar as equações
Agora, podemos igualar as duas expressões para (x):
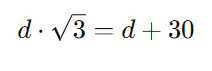
Passo 3: Resolver para (d)
Isolando (d):
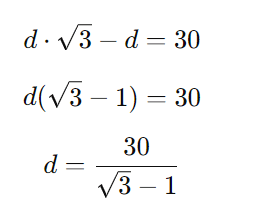
Passo 4: Racionalizar o denominador
Multiplicando numerador e denominador por √3 + 1:
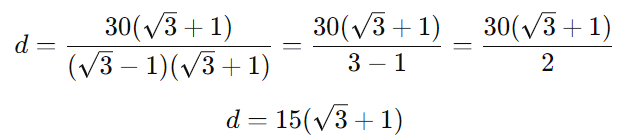
Passo 5: Substituir (d) em (x = d + 30)
Agora, substituímos (d) na equação (2):
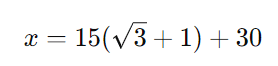
Passo 6: Aproximar valores
Sabemos que √3 = 1,732… , então:
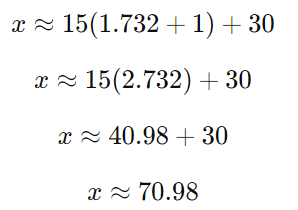
Resposta:
A altura do edifício é aproximadamente 71m.
[/toggle]
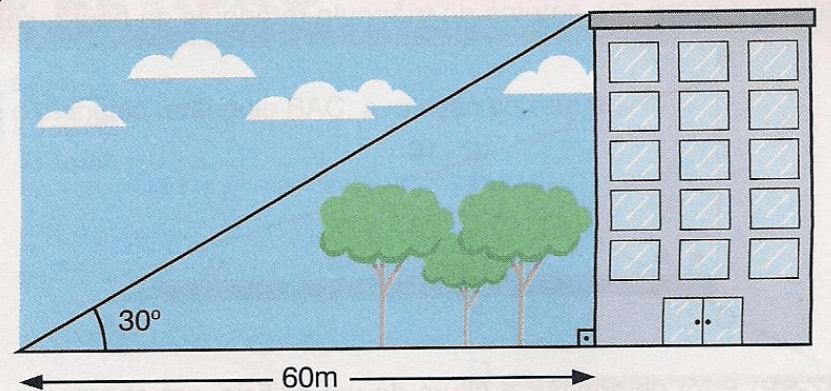
Exercícios 06 – Determine a altura do prédio da figura seguinte:
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
Vamos resolver o exercício usando a relação trigonométrica apropriada.
Dados fornecidos:
- Ângulo de elevação: (30°)
- Distância do observador ao prédio: (60m)
- Altura do prédio: (x) (a ser determinada)
Passo 1: Usar a tangente do ângulo
A tangente do ângulo de (30°) é dada pela razão entre a altura do prédio (x) e a distância ao prédio (60m):
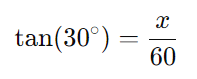
Sabemos que tan(30°) = 1/√3, então temos:
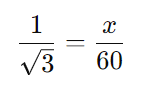
Passo 2: Resolver para (x)
Multiplicando ambos os lados da equação por 60:
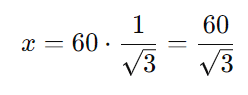
Racionalizando o denominador:
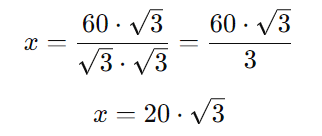
Passo 3: Aproximar o valor numérico
Sabemos que √3 = 1,732…, então:
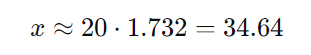
Resposta:
A altura do prédio é aproximadamente 34,64m.
[/toggle]
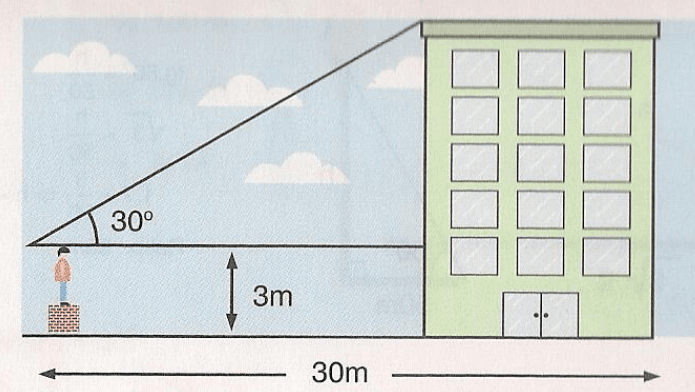
Exercícios 07 –Para determinar a altura de um edifício, um observador coloca – se a 30 m de distância e assim o observa segundo um ângulo de 30º, conforme mostra a figura. Calcule a altura do edifício medida a partir do solo horizontal. Dado √3 = 1,73
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
Vamos resolver este exercício passo a passo utilizando as razões trigonométricas.
Dados fornecidos:
- Distância do observador até o edifício: 30m
- Ângulo de elevação: 30°
- Altura da pessoa sobre o muro: 3 m
- Valor aproximado de √3 = 1,73
- Altura do edifício: (h) (a ser determinada)
Passo 1: Aplicar a tangente do ângulo
A tangente do ângulo de 30° é a relação entre a altura (x) do edifício (descontando os 3 m do muro) e a distância horizontal de 30m:
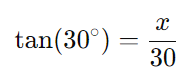
Sabemos que tan(30°) = 1/√3, então:
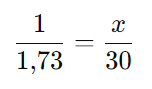
Passo 2: Resolver para (x)
Multiplicando ambos os lados da equação por 30:
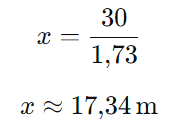
Passo 3: Somar a altura do muro
Agora, para encontrar a altura total do edifício (h), devemos somar a altura do muro de 3m:
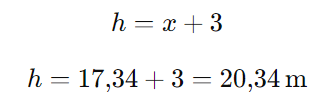
Resposta:
A altura do edifício é aproximadamente 20,34m.
[/toggle]
Exercícios 08 –Observe a figura e determine:
a) Qual é o comprimento da rampa?
b) Qual é a distância do inicio da rampa ao barranco?
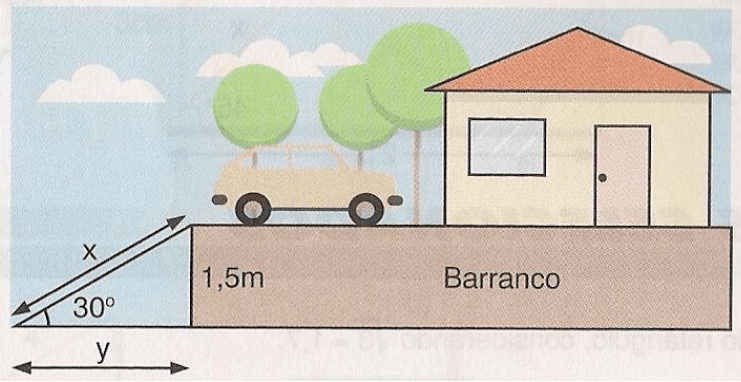
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
[/toggle]
Exercícios 09 – Determine qual era a altura do pinheiro da figura, considerando √3= 1,73
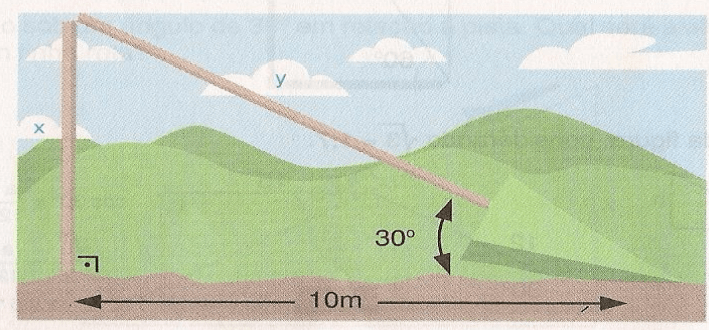
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
[/toggle]
Exercícios 10 – No triângulo retângulo determine as medidas x e y indicadas.(Use: sen 65º =
0,91; cos 65º = 0,42 e tg 65º = 2,14)
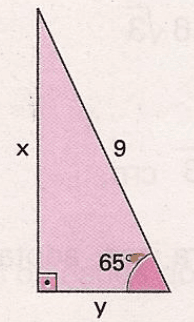
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
[/toggle]
Exercícios 11 – Determine no triângulo retângulo ABC as medidas a e c indicadas
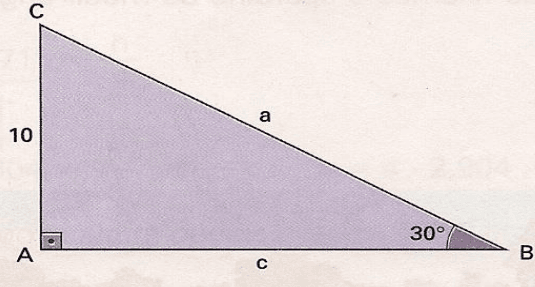
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
[/toggle]
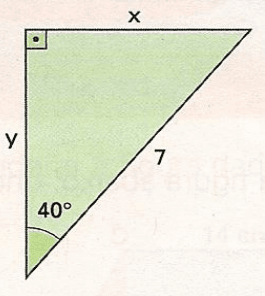
Exercícios 12 – Sabendo que sen 40º = 0,64; cos 40º = 0,77 e tg 40º = 0,84, determine as
medidas x e y indicadas no triângulo retângulo.
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
[/toggle]
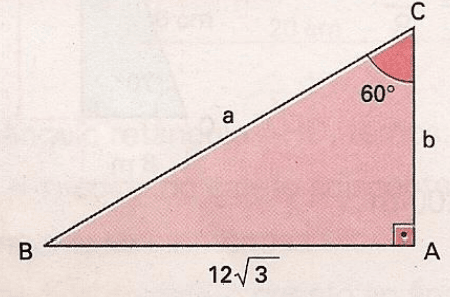
Exercícios 13 – Considerando o triângulo retângulo ABC, determine as medidas a e b indicadas.
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
[/toggle]
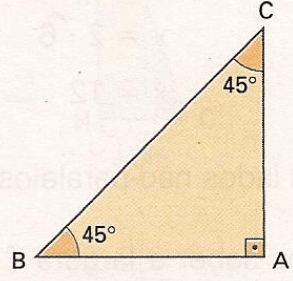
Exercícios 14 – Em um triângulo retângulo isósceles, cada cateto mede 30 cm. Determine a
medida da hipotenusa desse triângulo.
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
[/toggle]
Exercícios 15 – Sabe – se que, num triângulo isósceles, cada lado congruente mede 40 cm. Se cada ângulo da base desse triângulo mede 62º, determine:
a) a medida x da base;
b) a medida h da altura.
(Use: sen 62º = 0,88; cos 62º = 0,47; tg 62º = 1,88)
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
[/toggle]
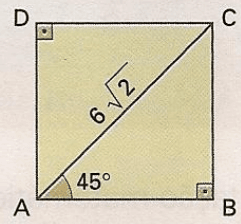
Exercícios 16 – A diagonal de um quadrado mede 6√2cm, conforme nos mostra a figura. Nessas condições, qual é o perímetro desse desse quadrado?
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
[/toggle]
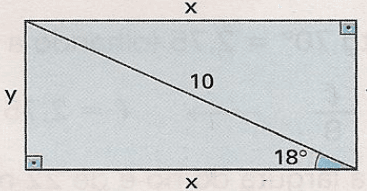
Exercícios 17 – A diagonal de um retângulo forma com o maior lado desse retângulo um ângulo de 18º, conforme mostra a figura. Se a diagonal mede 10 cm, determine as medidas x e y dos lados do retângulo, bem como o seu perímetro. (Use: sen 18º = 0,32; cos 18º = 0,95; tg 18º = 0,32.)
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
[/toggle]
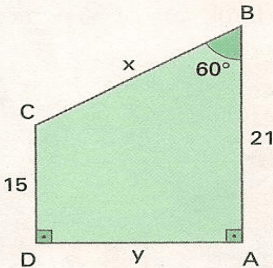
Exercícios 18 – A figura seguinte é um trapézio retângulo, sendo x e y as medidas dos lados não paralelos desse trapézio. Nessas condições, determine x e y.
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
[/toggle]
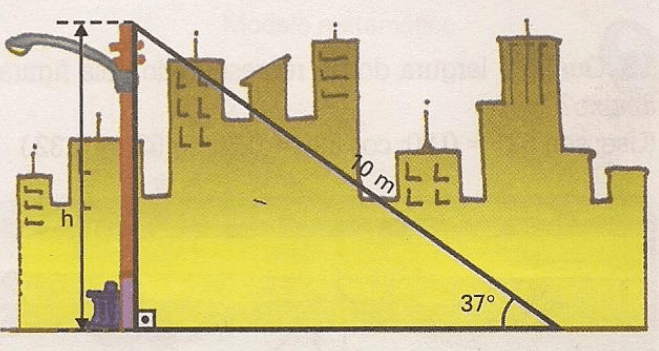
Exercícios 19 – Qual é a altura h do poste representado pela figura abaixo?
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
[/toggle]
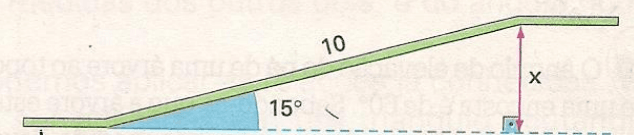
Exercícios 20 – Uma rampa lisa com 10 m de comprimento faz ângulo de 15º com o plano horizontal. Uma pessoa que sobe a rampa inteira eleva – se verticalmente a quantos metros?(Use: sen 15º = 0,26; cos 15º = 0,97; tg 15º = 0,27.)
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
[/toggle]
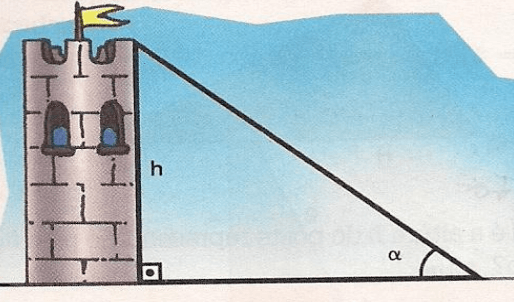
Exercícios 21 – A uma distância de 40 m, uma torre é vista sob um ângulo ∝, como nos mostra afigura. Determine a altura h da torre se:
a) ∝= 20º
b) ∝= 40º
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
[/toggle]
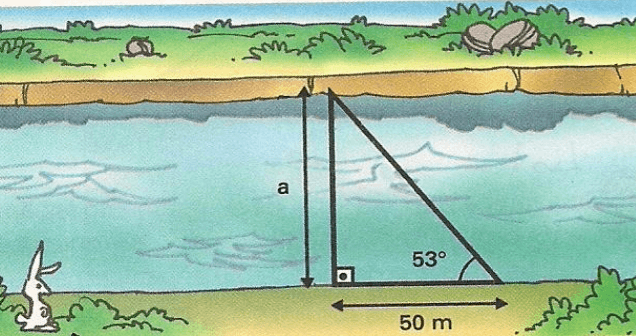
Exercícios 22 – Qual é a largura do rio representado pela figura abaixo?(Use: sen 53º = 0,80; cos 53º = 0,60; tg 53º = 1,32.)
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
[/toggle]
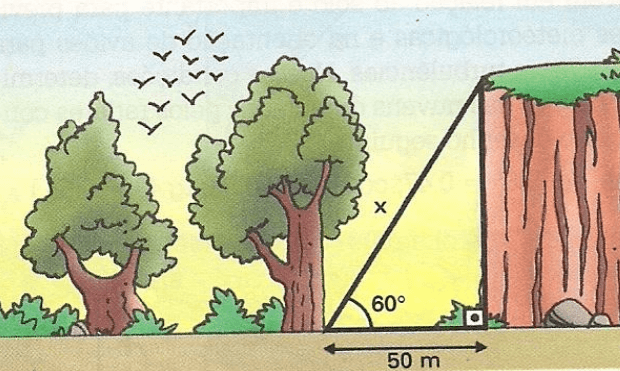
Exercícios 23 – O ângulo de elevação do pé de uma árvore ao topo de uma encosta é de 60º. Sabendo – se que a árvore está distante 50 m da base da encosta, que medida deve ter um cabo de aço para ligar a base da árvore ao topo da encosta?
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
[/toggle]













