Logaritmos: Propriedades, Exemplos Resolvidos e Aplicações

Logaritmos: Um Guia Didático Completo

Introdução ao Logaritmo

O conceito de logaritmo é um dos pilares fundamentais da matemática, com aplicações que vão desde a ciência e engenharia até a economia e a biologia. Em termos simples, um logaritmo é o inverso de uma exponenciação. Se você sabe que 2³ = 8, então você também sabe que o logaritmo de 8 na base 2 é 3, pois 2 elevado a 3 resulta em 8.

Definição Formal

Para um número real positivo a, um número real positivo b e um número real x, a equação:

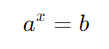
pode ser reescrita em termos de logaritmos como:

Aqui, a é a base do logaritmo, b é o número cujo logaritmo está sendo tomado, e x é o valor do logaritmo. Em palavras, log⁡_a(b) significa “o expoente ao qual a base a deve ser elevada para obter b.

O logaritmo é a inversa da exponencial

Bases Comuns

Existem duas bases de logaritmos amplamente utilizadas:

1. Logaritmo na base 10 (Logaritmo Decimal): Também chamado de logaritmo comum, é frequentemente usado em cálculos científicos e de engenharia. É denotado por log_⁡10(x) ou simplesmente log⁡(x).
2. Logaritmo na base eee (Logaritmo Natural): A base e (onde e ≈ 2.71828) é um número irracional, e o logaritmo natural é amplamente utilizado em matemática pura, cálculo e ciências. É denotado por log_⁡e(x).

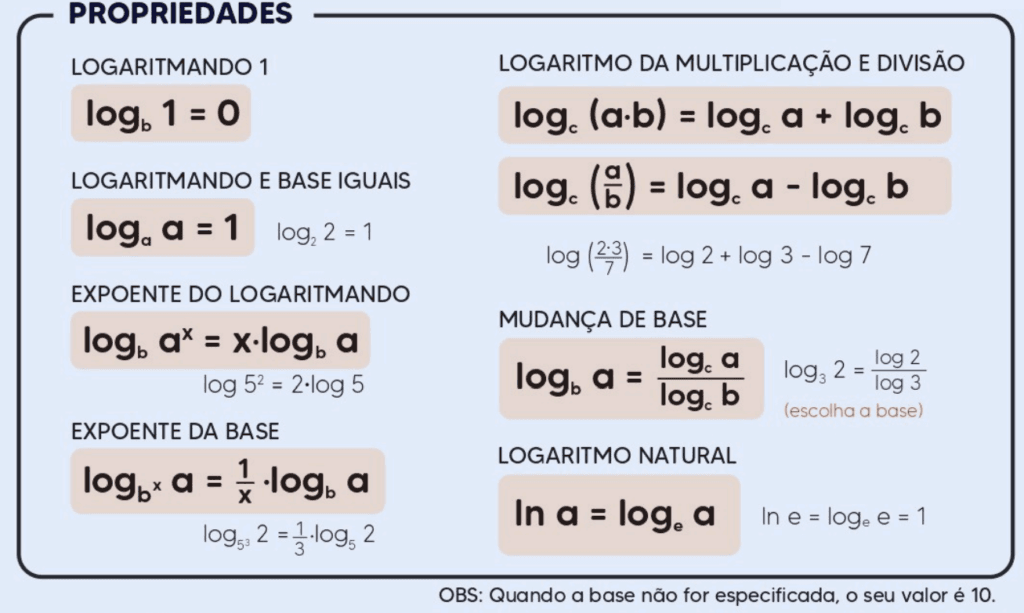
Propriedades dos Logaritmos

Os logaritmos possuem diversas propriedades importantes que facilitam a simplificação e resolução de problemas matemáticos. As principais propriedades são:

1. Propriedade do Produto: A propriedade do produto dos logaritmos estabelece que o logaritmo de um produto de dois números é igual à soma dos logaritmos desses números, ambos com a mesma base. Em outras palavras, para uma base a, a propriedade pode ser expressa como:

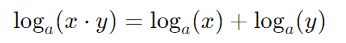
Essa propriedade é útil quando precisamos calcular logaritmos em uma base para a qual não temos uma tabela ou calculadora disponível.

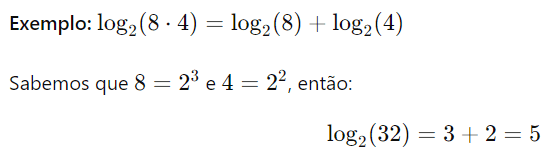
• Propriedade do Quociente: A propriedade do quociente dos logaritmos afirma que o logaritmo de um quociente entre dois números é igual à diferença entre os logaritmos desses números, ambos com a mesma base. Formalmente, para uma base aaa, essa propriedade é expressa como:

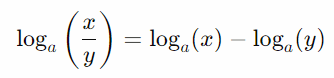
Essa propriedade é útil para simplificar expressões logarítmicas e resolver equações envolvendo divisões.

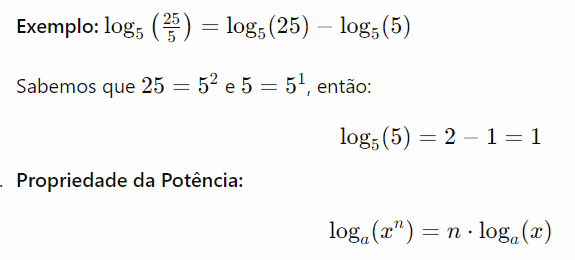
Propriedade da Potência: A propriedade da potência dos logaritmos estabelece que o logaritmo de um número elevado a um expoente é igual ao produto do expoente pelo logaritmo do número, ambos com a mesma base. Em termos formais, para uma base a, essa propriedade é dada por:

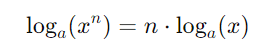
Essa propriedade facilita o processo de simplificação de expressões logarítmicas, especialmente quando lidamos com potências.

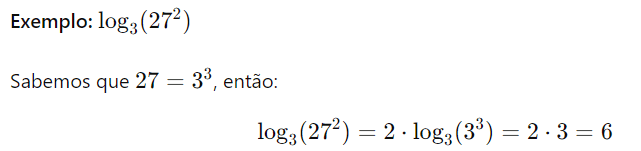
• Propriedade da Raiz: A propriedade da raiz dos logaritmos afirma que o logaritmo de uma raiz n-ésima de um número é igual ao logaritmo desse número dividido por n, ambos com a mesma base. Formalmente, para uma base a, essa propriedade pode ser expressa como:

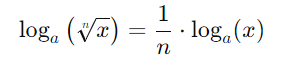
Essa propriedade é útil para simplificar expressões logarítmicas que envolvem raízes.

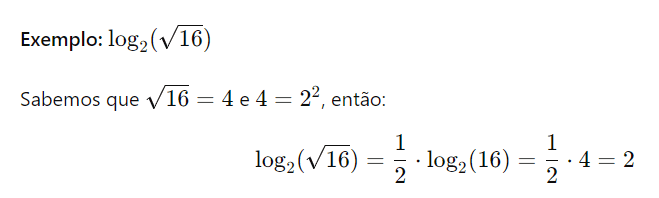
• Mudança de Base: A propriedade da mudança de base dos logaritmos permite calcular o logaritmo de um número em uma base diferente da original. Ela afirma que o logaritmo de um número x na base a pode ser expresso como a razão entre o logaritmo de x e o logaritmo de a em uma nova base b. Formalmente, a propriedade é dada por:

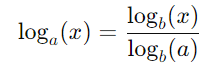
Essa propriedade é útil quando precisamos calcular logaritmos em uma base para a qual não temos uma tabela ou calculadora disponível.

Exercícios Propostos

Para fixar o conteúdo, seguem alguns exercícios com as soluções:

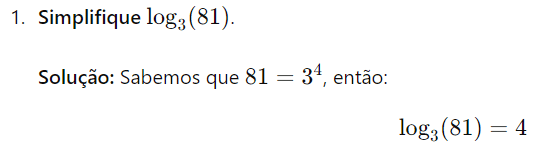
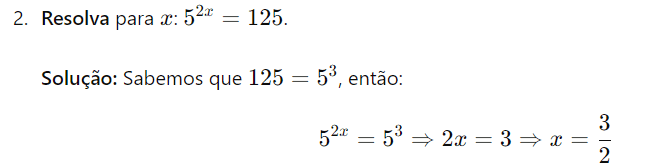
Logaritmos e a Escala Logarítmica

Além das propriedades algébricas, os logaritmos são cruciais para a compreensão de escalas logarítmicas, que são usadas quando precisamos lidar com números que variam em largas ordens de magnitude. Exemplos de escalas logarítmicas incluem:

• Escala Richter: Mede a magnitude dos terremotos.
• Escala de pH: Mede a acidez ou basicidade de uma solução.
• Decibéis: Usado para medir a intensidade do som.

Em uma escala logarítmica, um pequeno aumento no valor representa uma mudança significativa no fenômeno medido. Por exemplo, um aumento de 1 unidade na escala Richter corresponde a um terremoto com 10 vezes mais intensidade.

Lista de Exercícios: Logaritmos

Exercícios de Aplicação das Propriedades

1 – Simplifique a expressão log⁡₃(9⋅27)

2 – Calcule log⁡₅(125/25).

3 – Simplifique a expressão log⁡₂(16³).

4 – Calcule log⁡₇(∛343).

5 – Use a mudança de base para calcular log⁡₂(64), utilizando logaritmos na base 10.

Exercícios Práticos

6 – Determine o valor de x na equação 5^2x=125.

7 – Encontre o logaritmo de 32 na base 4.

8 – Resolva a equação log⁡₄(x)+log⁡₄(8)=5.

9 – Determine o valor de x na equação log⁡₉(81) = x.

10 – Simplifique a expressão 1/2⋅log⁡₆(36).

Desafios

11 – Encontre x na equação: 3^log_⁡3(x)=81.

12 – Resolva para x na equação log⁡₂(3x+5)=log⁡₂(32).

13 – Calcule y na equação log_⁡10(100y)=3+log⁡₁₀(y).

14 – Encontre o valor de x na expressão log_⁡x(64)=2.

15 – Determine o valor de n na expressão: n⋅log⁡₃(9)=log⁡3(81).

Logaritmos: Problemas Práticos e Soluções Detalhadas

1 – Crescimento Populacional:

Problema: A população de uma cidade cresce a uma taxa de 3% ao ano. Se a população atual é de 50.000 habitantes, em quantos anos a população dobrará?

Solução:

2 – Decaimento Radioativo:

Problema: Um material radioativo tem uma meia-vida de 20 anos. Se a quantidade inicial do material é de 100 gramas, quanto tempo levará para que restem apenas 25 gramas?

Solução:

3 – pH de uma Solução:

Problema: O pH de uma solução é dado por pH=−log⁡₁₀([H⁺]), onde [H⁺] é a concentração de íons de hidrogênio. Se uma solução tem uma concentração de íons de hidrogênio de 1×10⁻⁴¹ moles por litro, qual é o pH dessa solução?

Solução:

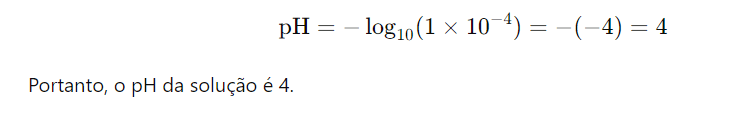
4 – Escala Richter:

Problema: A magnitude de um terremoto na escala Richter é dada por M=log_⁡10(A/A₀), onde A é a amplitude do movimento do solo e A₀​ é uma amplitude de referência. Se a amplitude de um terremoto foi 100.000100.000100.000 vezes maior que a referência, qual foi a magnitude do terremoto na escala Richter?

Solução:

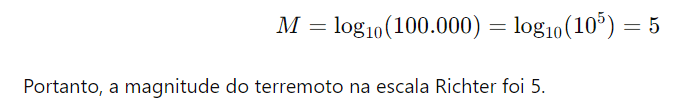
5 – Cálculo de Juros Compostos:

Problema: Um investimento de R$ 2.000,00 é feito a uma taxa de juros compostos de 5% ao ano. Quantos anos são necessários para que o investimento triplique de valor?

Solução:

6 – Efeito de Som no Ouvido:

Problema: O nível de intensidade sonora L em decibéis (dB) é dado por L=10⋅log⁡₁₀(I/I₀), onde III é a intensidade do som e I_0​ é a intensidade de referência. Se a intensidade de um som é 100010001000 vezes maior que a referência, qual é o nível de intensidade sonora em decibéis?

Solução:

7 – Depreciação de um Equipamento:

Problema: O valor de um equipamento deprecia a uma taxa de 10% ao ano. Se o valor inicial do equipamento é de R$ 10.000,00, em quantos anos o valor do equipamento será reduzido a R$ 2.500,00?

Solução:

8 – Difusão de Informação:

Problema: A difusão de uma informação em uma rede social segue o modelo N(t)=N₀⋅e^kt, onde N(t) é o número de pessoas que sabem da informação após t horas, N₀ é o número inicial de pessoas que sabiam da informação, e k é a constante de difusão. Se inicialmente 50 pessoas sabiam da informação e após 3 horas 200 pessoas ficaram sabendo, determine o valor de k.

Solução:

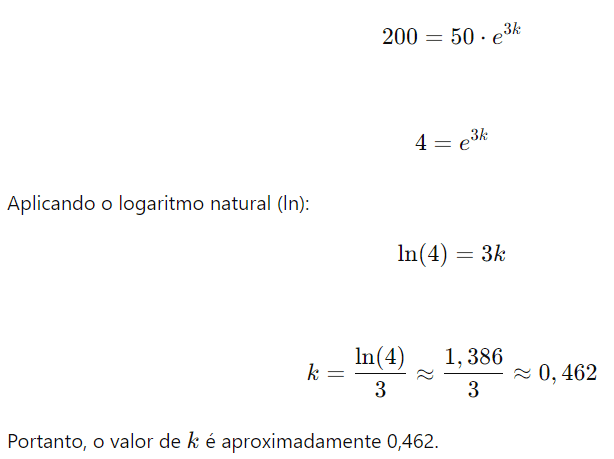
9 – Equilíbrio Químico:

Problema: Em uma reação química em equilíbrio, a constante de equilíbrio K é dada pela equação K=e^−G/RTK , onde GGG é a variação de energia livre, R é a constante universal dos gases e T é a temperatura. Se G=−5000 J/mol, R=8,314 J/mol K, e T=298 K, qual é o valor de K?

Solução:

10 – Escala de Magnitude Estelar:

Problema: A magnitude aparente de uma estrela é dada por m=−2,5⋅log⁡₁₀(I/I₀), onde I é a intensidade luminosa da estrela e I₀​ é uma intensidade de referência. Se a intensidade luminosa de uma estrela é 10⁶ vezes maior que a intensidade de referência, qual é a magnitude aparente dessa estrela?

Solução:

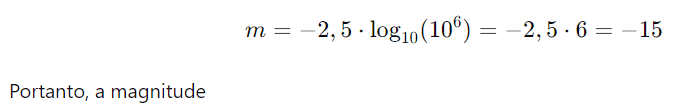
História dos Logaritmos

Os logaritmos foram uma das inovações matemáticas mais significativas do século XVII, revolucionando a maneira como cálculos complexos eram realizados. A criação dos logaritmos está intimamente ligada ao desenvolvimento de técnicas para simplificar cálculos aritméticos, especialmente aqueles relacionados à multiplicação e divisão de números grandes, essenciais para a navegação, astronomia e outras ciências.

Origens e Motivação

Antes da invenção dos logaritmos, cálculos que envolviam multiplicação, divisão e a extração de raízes eram feitos manualmente e eram extremamente demorados e sujeitos a erros. A motivação para simplificar esses cálculos levou ao desenvolvimento de várias técnicas ao longo do tempo, mas a solução definitiva veio com os logaritmos.

John Napier: O Pai dos Logaritmos

O crédito pela invenção dos logaritmos geralmente é dado ao matemático escocês John Napier (1550-1617), que publicou sua obra monumental “Mirifici Logarithmorum Canonis Descriptio” em 1614. Nesta obra, Napier introduziu o conceito de logaritmos como uma maneira de transformar multiplicações em somas e divisões em subtrações. Embora os logaritmos de Napier fossem diferentes dos que usamos hoje (os logaritmos naturais baseados em (e)), sua ideia fundamental foi o ponto de partida para o desenvolvimento posterior.

Napier definiu seus logaritmos em um contexto geométrico e não aritmético, utilizando progressões aritméticas e geométricas. Seu trabalho teve um impacto imediato na comunidade científica da época, facilitando cálculos em astronomia e navegação.

Henry Briggs e a Base 10

Pouco depois da publicação de Napier, o matemático inglês Henry Briggs (1561-1630) reconheceu o valor do trabalho de Napier e sugeriu uma modificação importante: a utilização da base 10, que se mostrou muito mais prática para os cálculos. Briggs trabalhou para calcular tabelas de logaritmos na base 10, que ficaram conhecidas como logaritmos comuns ou logaritmos decimais.

Em 1617, Briggs publicou a primeira tabela de logaritmos decimais, facilitando ainda mais os cálculos. As tabelas de Briggs foram utilizadas amplamente até o advento das calculadoras eletrônicas no século XX.

O Papel de Euler

No século XVIII, o matemático suíço Leonhard Euler (1707-1783) contribuiu significativamente para a teoria dos logaritmos. Euler foi o responsável por formalizar a definição de logaritmos naturais, baseados na constante (e ≂ 2,71828), que são fundamentais em muitas áreas da matemática moderna, como cálculo e análise.

Euler também ajudou a conectar os logaritmos a outras áreas da matemática, como as funções exponenciais e as séries infinitas, expandindo ainda mais o uso dos logaritmos em diversas disciplinas científicas.

A Evolução dos Logaritmos

Após as contribuições de Napier, Briggs e Euler, os logaritmos se tornaram uma ferramenta essencial em diversas áreas da ciência e da engenharia. Até meados do século XX, tabelas de logaritmos e réguas de cálculo (que utilizavam o princípio dos logaritmos) eram ferramentas indispensáveis para engenheiros, cientistas e navegadores.

Com o surgimento das calculadoras eletrônicas e, posteriormente, dos computadores, o uso de tabelas de logaritmos tornou-se obsoleto, mas o conceito matemático de logaritmos continua a ser fundamental em áreas como a análise matemática, a teoria da informação e a computação.

Conclusão

A história dos logaritmos é um testemunho do poder da inovação matemática para transformar a ciência e a tecnologia. A invenção dos logaritmos por John Napier, o refinamento por Henry Briggs e as contribuições teóricas de Leonhard Euler demonstram como ideias matemáticas podem evoluir e ter um impacto duradouro em diversas áreas do conhecimento humano. Hoje, os logaritmos são uma parte essencial da matemática, com aplicações que vão desde o cálculo de juros compostos até a modelagem de fenômenos naturais complexos.