Matemática Banca IBFC: Equação de 2º Grau – Questão Comentada

Confira questões resolvidas de Matemática da banca IBFC, organizadas e explicadas passo a passo. Ideal para quem busca praticar e entender os padrões dessa banca em concursos. Aperfeiçoe seus estudos com questões de matemática IBFC e melhore seu desempenho!

👉Livro Indicado Matemática para Concurso

(IBFC – 2023 – Equação de 2º Grau) Bhaskara Akaria (1114-1185) foi um matemático indiano que ficou conhecido por desenvolver a fórmula de Bhaskara, método utilizado na resolução de equações do segundo grau na forma  ax² +bx +c = 0 com a ≠ 0. Assim, dada a equação:

x² − x + 3√3− 5 = 0

Assinale a alternativa que apresenta o conjunto solução dessa equação.

A) S = {3 − √3, 1 − √3}

B) S = {−1 + 2√3,−√3}

C) S = {1 + √2, 2 − √2}

D) S = {−1 + √3, 2− √3}

Ver Solução

Para resolver a equação x² − x + 3√3− 5 = 0 e encontrar o conjunto solução, vamos aplicar a fórmula de Bhaskara:

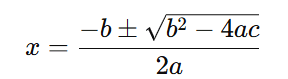
onde, para a equação ( ax² + bx + c = 0 ):

• ( a = 1 )
• ( b = -1 )
• ( c = 3√3− 5 )

Passo 1: Calcular o discriminante (Δ)

O discriminante Δ é dado por:

Δ = b² – 4ac

Substituindo os valores:

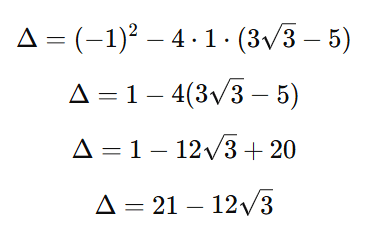
Passo 2: Substituir na fórmula de Bhaskara

Agora, usando a fórmula de Bhaskara:

Confira a Simplificação de:

Aqui

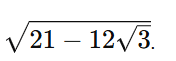
Substituindo os valores

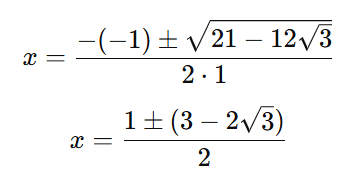
Agora, vamos separar as duas soluções:

Primeira solução

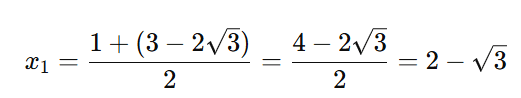
Segunda solução

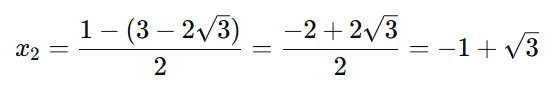
Conjunto solução

O conjunto solução é:

Resposta

Alternativa correta: D)

Gostou da explicação? Continue praticando com mais questões matemática IBFC, e confira um Livro de Matemática indicado.

🟣Questões de Matemática IBFC (Nível Fundamental) – PDF Exclusivo para Concursos

🟠Questões de Matemática IBFC (Nível Médio) – PDF Exclusivo para Concursos

🔴Questões de Matemática IBFC (Nível Superior) – PDF Exclusivo para Concursos

🟢Mapas Mentais de Matemática para Concurso

👉Entre no nosso canal do WhatsApp

📘 Todas as fórmulas de matemática em um só lugar! Baixe agora nosso eBook gratuito