Confira questões resolvidas de Matemática da banca IBFC, organizadas e explicadas passo a passo. Ideal para quem busca praticar e entender os padrões dessa banca em concursos. Aperfeiçoe seus estudos com questões de matemática IBFC e melhore seu desempenho!
👉Livro Indicado Matemática para Concurso
(IBFC – 2023 – Função Exponencial) A equação geral da reta que passa pelos pontos A e B, sendo considerado a função ƒ(x) = 2x, é igual a:
A) 2x – 3y – 2 = 0
B) 2y – 3x – 2 = 0
C) -2x + 3y + 2 = 0
D) 3y – 3x + 4 = 0
E) 2x – 3y – 7 = 0
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
Peço desculpas pelo engano! Vamos revisar a solução com atenção aos sinais e à forma correta.
Passo 1: Identificar as coordenadas dos pontos ( A ) e ( B )
Como vimos antes, os pontos ( A ) e ( B ) são:
- ( A = (0, 1) )
- ( B = (2, 4) ) ⇨ ƒ(x) = 2x ⇨ ƒ(2) = 22 = 4
Passo 2: Calcular o coeficiente angular ( m )
O coeficiente angular ( m ) é:
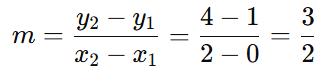
Passo 3: Determinar a equação da reta
Usando o ponto ( A(0, 1) ) na forma ponto-inclinação y – y1 = m(x – x1):
y – 1 = 3/2x
Multiplicando todos os termos por 2 para eliminar o denominador:
2y – 2 = 3x
Colocando na forma geral:
2y – 3x – 2 = 0
Conclusão
A equação correta da reta que passa pelos pontos ( A ) e ( B ) é:
A correta é: 2y – 3x – 2 = 0
Logo Letra B
Gostou da explicação? Continue praticando com mais questões matemática IBFC, e confira um Livro de Matemática indicado.
[/toggle]
🟣Questões de Matemática IBFC (Nível Fundamental) – PDF Exclusivo para Concursos
🟠Questões de Matemática IBFC (Nível Médio) – PDF Exclusivo para Concursos
🔴Questões de Matemática IBFC (Nível Superior) – PDF Exclusivo para Concursos
🟢Mapas Mentais de Matemática para Concurso