Matemática Banca IBFC: Polinômios – Questão Comentada

Confira questões resolvidas de Matemática da banca IBFC, organizadas e explicadas passo a passo. Ideal para quem busca praticar e entender os padrões dessa banca em concursos. Aperfeiçoe seus estudos com questões de matemática IBFC e melhore seu desempenho!

👉Livro Indicado Matemática para Concurso

(Banca IBFC – 2021 – Polinômios) Considere a igualdade polinomial dada por 

∀x ∈ ℂ − {−1,0, 1}, assinale a alternativa que apresenta o valor numérico de a + b + c.

A) 2

B) -1

C) 1

D) 0

[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]

Para resolver completamente essa questão, vamos desenvolver o processo de igualar os coeficientes de forma detalhada.

A igualdade polinomial dada é:

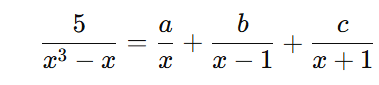
Primeiro, fatoramos o denominador do lado esquerdo:

x³ – x = x(x – 1)(x + 1)

Assim, a equação se torna:

Para igualar os denominadores, precisamos escrever o lado direito como uma única fração com o mesmo denominador x(x – 1)(x + 1):

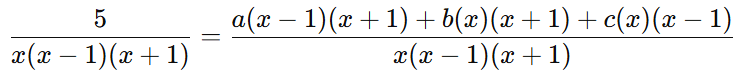
Igualando os numeradores:

5 = a(x – 1)(x + 1) + b(x)(x + 1) + c(x)(x – 1)

Agora, expandimos cada termo do lado direito:

1. Expansão de a(x – 1)(x + 1):
   
   a(x – 1)(x + 1) = a(x² – 1) = ax² – a
   
2. Expansão de b(x)(x + 1):
   
   b(x)(x + 1) = b(x² + x) = bx² + bx
   
3. Expansão de ( c(x)(x – 1) ):
   
   c(x)(x – 1) = c(x² – x) = cx² – cx
   

Somando todos os termos, temos:

5 = (a + b + c)x² + (b – c)x – a

Agora, comparamos os coeficientes de cada termo com o lado esquerdo, que é 5 = 0 ⋅ x² + 0 ⋅ x + 5 . Assim, obtemos o seguinte sistema de equações:

1. Coeficiente de ( x² ): a + b + c = 0
2. Coeficiente de ( x ): b – c = 0
3. Termo constante: -a = 5

Resolvendo o sistema:

1. Da terceira equação, temos a = -5.
2. Substituindo a = -5 na primeira equação:
   
   -5 + b + c = 0 ⇒ b + c = 5
   
3. Da segunda equação, temos b = c .

Substituindo b = c na equação b + c = 5:

2b = 5 ⇒ b = 5/2

Como b = c, então c = 5/2.

Portanto, encontramos a = -5, b = 5/2, e c = 5/2.

Agora, somamos a + b + c:

A resposta final é:

D) 0

Gostou da explicação? Continue praticando com mais questões matemática IBFC, e confira um Livro de Matemática indicado.

[/toggle]

🟣Questões de Matemática IBFC (Nível Fundamental) – PDF Exclusivo para Concursos

🟠Questões de Matemática IBFC (Nível Médio) – PDF Exclusivo para Concursos

🔴Questões de Matemática IBFC (Nível Superior) – PDF Exclusivo para Concursos

🟢Mapas Mentais de Matemática para Concurso