Matemática Banca IBFC: Probabilidade – Questão Comentada

Para resolver esse problema, precisamos calcular a probabilidade de que, em uma mesa escolhida aleatoriamente, existam exatamente 2 pessoas alérgicas a glúten. Vamos analisar as informações fornecidas:

• Total de convidados: 40
• Número de alérgicos a glúten: 16
• Número de mesas: 8
• Distribuição dos convidados: Cada mesa possui 40/8 = 5 pessoas.

Podemos resolver essa questão usando o conceito de distribuição binomial, pois estamos interessados na probabilidade de um certo número de sucessos (pessoas alérgicas) em um número fixo de tentativas (lugares na mesa).

Parâmetros da distribuição binomial

Para a distribuição binomial, temos:

• ( n = 5 ): número de pessoas na mesa
• ( x = 2 ): queremos exatamente 2 pessoas alérgicas
• ( p ): probabilidade de uma pessoa ser alérgica a glúten
• ( q = 1 – p ): probabilidade de uma pessoa não ser alérgica a glúten

A probabilidade ( p ) de uma pessoa ser alérgica é dada por:

e, portanto, ( q = 1 – 0,4 = 0,6 ).

Cálculo da Probabilidade

A fórmula para a probabilidade binomial é:

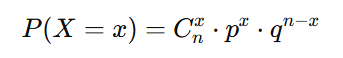
onde

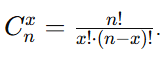
Substituindo os valores:

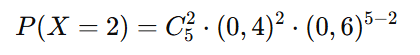
Coeficiente binomial: C(5,2) = 10

Probabilidade binomial: 10 × (0,4)² × (0,6)³ = 0,3456

Convertendo para percentual: 0,3456 × 100 = 34,56%

Agora, vamos calcular esse valor.

A probabilidade de escolhermos uma mesa com exatamente 2 pessoas alérgicas a glúten é de 34,56%.

Portanto, a alternativa correta é:

B) 34,56%

Gostou da explicação? Continue praticando com mais questões matemática IBFC, e confira um Livro de Matemática indicado.