A matemática é um dos pilares dos concursos públicos e, para o concurso dos Correios, não é diferente. Dominar os conteúdos de matemática pode ser o diferencial entre o sucesso e a reprovação, especialmente quando se trata de resolver questões que exigem agilidade, precisão e entendimento dos conceitos fundamentais. Este material foi desenvolvido especialmente para candidatos que desejam se preparar de maneira eficaz e objetiva para o concurso dos Correios. Com uma abordagem prática e detalhada, apresentamos uma seleção de questões comentadas que abrangem os tópicos mais recorrentes, explicando passo a passo as soluções para que o candidato compreenda tanto o raciocínio quanto as técnicas de resolução. Além de fortalecer o conhecimento matemático, este material ajuda a aprimorar as habilidades de resolução de problemas, oferecendo uma preparação completa e direcionada para enfrentar a prova com confiança e clareza.
01 – (CESPE – Correios – 2011) O piso de uma sala retangular, medindo 3,52 m × 4,16 m, será revestido com ladrilhos quadrados, de mesma dimensão, inteiros, de forma que não fique espaço vazio entre ladrilhos vizinhos. Os ladrilhos serão escolhidos de modo que tenham a maior dimensão possível.
Se, para assentar os ladrilhos, são utilizados 2 kg de argamassa por m2 e se a argamassa é vendida em sacos de 3 kg, então a quantidade necessária de sacos de argamassa para completar o serviço é igual a
A) 9.
B) 10.
C) 6.
D) 7.
E) 8.
Ver Solução
- Determinar o lado dos ladrilhos:
- A sala mede 3,52 m × 4,16 m. Convertendo para centímetros: 352 cm × 416 cm.
- Calculamos o MDC de 352 e 416, que é 32 cm. Assim, o lado do ladrilho quadrado será de 0,32 m.
- MDC(352, 416) = 32 cm ⇒ lado do ladrilho = 0,32 m
- Calcular a quantidade de ladrilhos necessários:
- Área da sala:
3,52×4,16 = 14,6432 m2 - Área de um ladrilho:
0,32×0,32 = 0,1024 m2 - Número de ladrilhos:
14,6432/0,1024 = 143,04⇒arredondando, são necessários 144 ladrilhos
- Calcular a quantidade de argamassa necessária:
- Cada metro quadrado precisa de 2 kg de argamassa:
14,6432×2 = 29,2864 kg - A argamassa é vendida em sacos de 3 kg, então:
29,2864/3 = 9,762 ⇒ arredondando, são necessários 10 sacos
Resposta: B) 10
02 – (CESPE – Correios – 2011) O piso de uma sala retangular, medindo 3,52 m × 4,16 m, será revestido com ladrilhos quadrados, de mesma dimensão, inteiros, de forma que não fique espaço vazio entre ladrilhos vizinhos. Os ladrilhos serão escolhidos de modo que tenham a maior dimensão possível.
Na situação apresentada, o lado do ladrilho deverá medir
A) mais de 30 cm.
B) menos de 15 cm.
C) mais de 15 cm e menos de 20 cm.
D) mais de 20 cm e menos de 25 cm.
E) mais de 25 cm e menos de 30 cm.
Ver Solução
Para resolver essa questão, precisamos encontrar o maior valor possível para o lado dos ladrilhos quadrados, de forma que eles se encaixem perfeitamente na sala. O lado do ladrilho será o Máximo Divisor Comum (MDC) das dimensões da sala em centímetros.
Passo 1: Converter as medidas para centímetros
As medidas da sala são:
- 3,52 m = 352 cm
- 4,16 m = 416 cm
Passo 2: Calcular o MDC de 352 e 416
Usamos o MDC para encontrar o maior tamanho possível dos ladrilhos que se encaixem perfeitamente nessas dimensões.
- Decompondo 352 em fatores primos: 352=25×11
- Decompondo 416 em fatores primos: 416=25×13
O maior divisor comum entre 352 e 416 é 25=32 Portanto, o lado do ladrilho deverá ser 32 cm.
Passo 3: Analisar a alternativa correta
Sabemos que o lado do ladrilho será 32 cm, o que corresponde à opção:
Alternativa correta: A) mais de 30 cm.
03 – (CESPE – Correios – 2011) Em 2/3/2011, Steve Jobs, executivo-chefe da Apple, apresentou em São Francisco o iPad2, o segundo modelo do seu tablet iPad. Lançado em abril de 2010, o iPad tornou-se o mais bem-sucedido produto eletrônico de consumo da história, com 14,8 milhões de unidades vendidas em apenas um ano. Entre as inovações presentes no iPad2, destaca-se a redução de sua espessura, que passou de 13,4 mm para 8,8 mm. O impacto do lançamento do iPad2 fez que as ações da Apple na Nasdaq, a bolsa de tecnologia de Nova York, subissem 1% no dia do lançamento, tendo alcançado 352 dólares.
Veja, 9/3/2011, p. 74-5 (com adaptações).
Se em 1.º/3/2011, 1 dólar valia R$ 1,64, então, nessa data, de acordo com o texto, uma ação da Apple valia
A) mais de R$ 500,00 e menos de R$ 600,00.
B) mais de R$ 600,00 e menos de R$ 700,00.
C) mais de R$ 700,00 e menos de R$ 800,00.
D) mais de R$ 800,00.
E) menos de R$ 500,00.
Ver Solução
Para resolver essa questão, basta converter o valor da ação da Apple em dólares para reais usando a taxa de câmbio dada.
Passo 1: Valor da ação em dólares
De acordo com o texto, no dia do lançamento do iPad2, o valor de uma ação da Apple na Nasdaq era de 352 dólares.
Passo 2: Taxa de câmbio
No dia 1.º de março de 2011, 1 dólar valia R$ 1,64.
Passo 3: Calcular o valor da ação em reais
Multiplicamos o valor da ação em dólares pela taxa de câmbio para obter o valor em reais:
352 x 1,64 = 577,28
Passo 4: Analisar a alternativa correta
O valor de uma ação da Apple em reais era de R$ 577,28, que se enquadra na faixa de mais de R$ 500,00 e menos de R$ 600,00.
Alternativa correta: A) mais de R$ 500,00 e menos de R$ 600,00.
04 – (CESPE – Correios – 2011) Em 2/3/2011, Steve Jobs, executivo-chefe da Apple, apresentou em São Francisco o iPad2, o segundo modelo do seu tablet iPad. Lançado em abril de 2010, o iPad tornou-se o mais bem-sucedido produto eletrônico de consumo da história, com 14,8 milhões de unidades vendidas em apenas um ano. Entre as inovações presentes no iPad2, destaca-se a redução de sua espessura, que passou de 13,4 mm para 8,8 mm. O impacto do lançamento do iPad2 fez que as ações da Apple na Nasdaq, a bolsa de tecnologia de Nova York, subissem 1% no dia do lançamento, tendo alcançado 352 dólares.
Veja, 9/3/2011, p. 74-5 (com adaptações).
De acordo com as informações do texto, a espessura do iPad2, em relação à espessura do iPad lançado em 2010, foi reduzida em
A) mais de 1/4 e menos de 1/3 .
B) mais de 1/3 e menos de 1/2 .
C) mais de 1/2.
D) menos de 1/5.
E) mais de 1/5 e menos de 1/4.
Ver Solução
Para calcular a redução da espessura do iPad2 em relação ao modelo anterior, usaremos a diferença entre as espessuras e depois encontraremos a proporção dessa redução em relação à espessura inicial.
Passo 1: Determinar a diferença de espessura
A espessura do modelo original do iPad era de 13,4 mm, e a do iPad2 é de 8,8 mm. A redução na espessura é:
13,4 mm − 8,8 mm = 4,6 mm
Passo 2: Calcular a proporção da redução em relação à espessura inicial
Para encontrar a fração correspondente à redução, dividimos a diferença pela espessura inicial:
4,6/13,4 ≈ 0,3433
Passo 3: Converter o valor decimal para fração aproximada
O valor decimal 0,3433 é equivalente a aproximadamente 34,33%, ou seja, mais de 1/3 (33,33%) e menos de 1/2 (50%).
Análise da alternativa correta
A redução na espessura do iPad2 foi, portanto, mais de 1/3 e menos de 1/2.
Alternativa correta: B) mais de 1/3 e menos de 1/2.
05 – (CESPE – Correios – 2011) Em 10/01/2011, os Correios lançaram selo comemorativo de data histórica, com tiragem de 900.000 unidades. Do dia 1. o ao dia 10 de janeiro, foram vendidas 210.630 unidades desses selos, das quais 1.958 foram vendidas apenas no dia 4, primeiro dia de comercialização do selo via Internet. O prazo de comercialização desse selo pelos Correios vigorará até 31/12/2014.
Com base nas informações do texto acima e considerando-se que o ritmo de venda do selo tenha sido mantido ao longo do mês de janeiro de 2011, é correto afirmar que a quantidade de selos vendidos, em milhares de unidades, até o dia 30 do referido mês, foi
A) superior a 640.
B) inferior a 610.
C) superior a 610 e inferior a 620.
D) superior a 620 e inferior a 630.
E) superior a 630 e inferior a 640.
Ver Solução
Para resolver essa questão, vamos estimar o total de selos vendidos até o dia 30 de janeiro, assumindo que o ritmo de venda se manteve constante ao longo do mês.
Passo 1: Determinar a média de vendas diárias
Entre os dias 1 e 10 de janeiro, foram vendidas 210.630 unidades. Portanto, a média de vendas diárias nesses 10 dias foi:
210.630/10 = 21.063 selos por dia
Passo 2: Estimar as vendas até o dia 30 de janeiro
Se o ritmo de venda de 21.063 selos por dia foi mantido, então o total de selos vendidos até o dia 30 (30 dias) seria:
21.063 x 30 = 631.890 selos
Passo 3: Analisar a alternativa correta
A quantidade de selos vendidos até o dia 30 de janeiro foi de aproximadamente 631.890, o que está entre 630 mil e 640 mil.
Alternativa correta: E) superior a 630 e inferior a 640.
06 – (CESPE – Correios – 2011) Nos Correios, são utilizados vários tipos de caixas para o envio de encomendas, entre elas, a caixa do tipo 4B, um paralelepípedo retângulo, em papel ondulado, com arestas medindo 360 mm, 270 mm e 180 mm.
O volume dessa caixa, em dm3 , é
A) superior a 18 e inferior a 21.
B) superior a 21 e inferior a 24.
C) superior a 24.
D) inferior a 15.
E) superior a 15 e inferior a 18.
Ver Solução
Para calcular o volume de uma caixa do tipo 4B, que é um paralelepípedo retângulo, utilizamos a fórmula do volume:
V = a × b × c
onde (a), (b) e (c) são as dimensões da caixa.
Passo 1: Determinar as dimensões
As dimensões da caixa são:
- (a = 360 mm)
- (b = 270 mm)
- (c = 180 mm)
Passo 2: Calcular o volume em mm³
Substituindo os valores na fórmula:
V = 360 × 270 × 180
Calculando:
- 360 × 270 = 97.200mm2
- 7.200 × 180 = 17.556.000mm3
Passo 3: Converter mm³ para dm³
Sabemos que 1dm3=1.000.000mm3. Portanto, para converter o volume de mm³ para dm³, dividimos por 1.000.000:
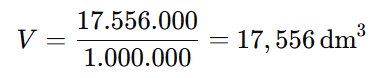
Passo 4: Analisar a alternativa correta
O volume da caixa é aproximadamente 17,556 dm³, que está entre 15 e 18.
Alternativa correta: E) superior a 15 e inferior a 18.
07 – (CESPE – Correios – 2011) Em 2008, nos 200 anos do Banco do Brasil, os Correios lançaram um selo comemorativo com uma tiragem de 1.020.000 unidades. No selo, cujo formato é de um retângulo medindo 40 mm × 30 mm, a estampa ocupa um retângulo que mede 35 mm × 25 mm.
Dadas essas condições, é correto afirmar que a área do retângulo da estampa é
A) superior a 90% da área do retângulo do selo.
B) inferior a 75% da área do retângulo do selo.
C) superior a 75% e inferior a 80% da área do retângulo do selo.
D) superior a 80% e inferior a 85% da área do retângulo do selo.
E) superior a 85% e inferior a 90% da área do retângulo do selo.
Ver Solução
Para resolver essa questão, precisamos calcular a área do retângulo do selo e a área do retângulo da estampa, e depois determinar a porcentagem que a área da estampa representa em relação à área do selo.
Passo 1: Calcular a área do selo
As dimensões do selo são:
- Comprimento: 40 mm
- Largura: 30 mm
A área (As) do selo é dada por:
Passo 2: Calcular a área da estampa
As dimensões da estampa são:
- Comprimento: 35 mm
- Largura: 25 mm
A área (Ae) da estampa é dada por:
Passo 3: Calcular a porcentagem da área da estampa em relação à área do selo
Para encontrar a porcentagem que a área da estampa representa em relação à área do selo, usamos a seguinte fórmula:
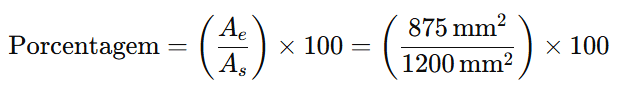
Calculando:
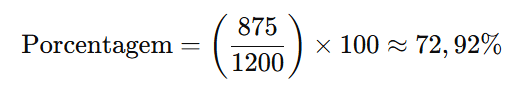
Passo 4: Analisar a alternativa correta
A área da estampa representa aproximadamente 72,92% da área do selo, que é inferior a 75%.
Alternativa correta: B) inferior a 75% da área do retângulo do selo.
08 – (CESPE – Correios – 2011) Além da missão de entregar correspondências, os carteiros são também responsáveis pela difusão de importantes campanhas de conscientização da população e promoção da cidadania. Um exemplo de ação de caráter social que envolve os carteiros e que tem tido grande receptividade é o projeto Papai Noel dos Correios. Em 2009, foram adotados 21% das 1.981.000 cartas recebidas pelos Correios. O projeto contou com o apoio e a participação de 3.818 voluntários internos, 669 voluntários externos e 462 parcerias.
Se, em 2010, o projeto Papai Noel dos Correios contou com 22.435 voluntários, e se foi mantida a mesma proporção de voluntários externos e internos verificada em 2009, então a quantidade de voluntários internos em 2010 foi
A) superior a 19.050 e inferior a 19.100.
B) superior a 19.100 e inferior a 19.150.
C) superior a 19.150.
D) inferior a 19.000.
E) superior a 19.000 e inferior a 19.050.
Ver Solução
Para calcular a quantidade de voluntários internos em 2010 com base na proporção de voluntários internos e externos de 2009, vamos seguir os passos abaixo.
Passo 1: Calcular a quantidade total de voluntários em 2009
Em 2009, o projeto teve:
- Voluntários internos: 3.818
- Voluntários externos: 669
A quantidade total de voluntários em 2009 é:
Total de voluntários em 2009 = 3.818 + 669 = 4.487
Passo 2: Determinar a proporção de voluntários internos e externos
Agora, vamos calcular a proporção de voluntários internos em relação ao total de voluntários em 2009:
A proporção de voluntários externos é:
Passo 3: Aplicar a mesma proporção em 2010
Em 2010, o projeto contou com 22.435 voluntários. Vamos agora calcular a quantidade de voluntários internos para esse total, usando a proporção encontrada:
Quantidade de voluntários internos em 2010 = 0,8514 × 22.435 ≈ 19.078
Passo 4: Analisar a alternativa correta
A quantidade de voluntários internos em 2010 foi de aproximadamente 19.078, que está superior a 19.050 e inferior a 19.100.
Alternativa correta: A) superior a 19.050 e inferior a 19.100.
09 – (CESPE – Correios – 2011) Além da missão de entregar correspondências, os carteiros são também responsáveis pela difusão de importantes campanhas de conscientização da população e promoção da cidadania. Um exemplo de ação de caráter social que envolve os carteiros e que tem tido grande receptividade é o projeto Papai Noel dos Correios. Em 2009, foram adotados 21% das 1.981.000 cartas recebidas pelos Correios. O projeto contou com o apoio e a participação de 3.818 voluntários internos, 669 voluntários externos e 462 parcerias.
Com base no texto, é correto afirmar que, em 2009, a quantidade de cartas que não foram adotadas pelo projeto Papai Noel dos Correios foi
A) superior a 1,2 milhão e inferior a 1,3 milhão.
B) superior a 1,3 milhão e inferior a 1,4 milhão.
C) superior a 1,4 milhão e inferior a 1,5 milhão.
D) superior a 1,5 milhão.
E) inferior a 1,2 milhão.
Ver Solução
Para determinar a quantidade de cartas que não foram adotadas pelo projeto Papai Noel dos Correios em 2009, vamos seguir os passos abaixo.
Passo 1: Calcular a quantidade de cartas adotadas
O texto afirma que foram adotados 21% das 1.981.000 cartas. Vamos calcular a quantidade de cartas adotadas:
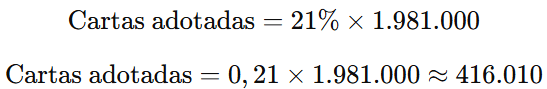
Passo 2: Calcular a quantidade de cartas que não foram adotadas
Agora, subtraímos a quantidade de cartas adotadas do total de cartas recebidas:
Passo 3: Analisar as alternativas
Agora, analisamos a quantidade de cartas não adotadas:
- A) superior a 1,2 milhão e inferior a 1,3 milhão. (FALSO)
- B) superior a 1,3 milhão e inferior a 1,4 milhão. (FALSO)
- C) superior a 1,4 milhão e inferior a 1,5 milhão. (FALSO)
- D) superior a 1,5 milhão. (VERDADEIRO)
- E) inferior a 1,2 milhão. (FALSO)
Conclusão
A quantidade de cartas que não foram adotadas pelo projeto Papai Noel dos Correios em 2009 foi superior a 1,5 milhão. Portanto, a alternativa correta é:
D) superior a 1,5 milhão.
10 – Um número mais sua metade mais sua quarta parte é igual a 63. Esse número é
A) 30
B) 36
C) 32
D) 38
E) 34
Ver Solução
Um número mais sua metade mais sua quarta parte é igual a 63. Vamos resolver a equação:
Passo a Passo:
Definimos o número como ( x ).
Montamos a equação:
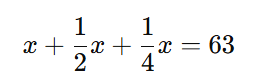
Somamos os termos semelhantes:
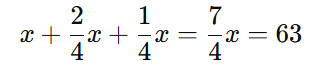
Isolamos ( x ):
Conclusão
O número é 36. Portanto, a alternativa correta é B) 36.
Lista Para o Concurso dos Correios 1
Lista Para o Concurso dos Correios 1
Lista Para o Concurso dos Correios 1
