Confira a resolução detalhada de uma questão típica da banca VUNESP. Entenda o método e prepare-se para suas provas com confiança.
(Banca VUNESP – Nível Médio – 2023 – Geometria Plana) O terreno A, cuja forma é uma composição de retângulos, e o terreno B, cuja forma é um triângulo retângulo, apresentam as medidas apresentadas nas figuras que estão expressas fora de escala.
Sabe-se que a área do terreno B supera em 20% a área do terreno A. Desse modo, é correto determinar que o valor da medida y, em metros, é um número entre
A) 19 e 20.
B) 20 e 21.
C) 21 e 22.
D) 22 e 23.
E) 23 e 24.
Ver Solução
Figura A: Área do Terreno
A área do terreno AA é formada por dois retângulos:
- Retângulo 1: 5×11=55 m2
- Retângulo 2: 4×4=16 m2
Somando as áreas:
Área de A = 55 + 16 = 71 m2
Figura B: Cálculo da Área
A área do terreno BB é 20% maior que a área do terreno A. Calculamos:
Área de B = 71 × 1,2 = 85,2 m2
Determinar a base y do triângulo BB
A fórmula da área do triângulo é:
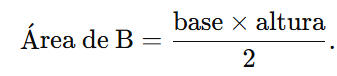
Substituímos os valores conhecidos:
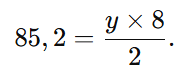
Multiplicamos ambos os lados por 2:
170,4 = 8y
Dividimos por 8:
y = 170,4/8 = 21,3 m
Conclusão
A medida de y está entre 21 e 22.
Resposta correta: C) 21 e 22.
Gostou desta questão? Confira outras questões resolvidas de Matemática VUNESP aqui.
👉Entre no nosso canal do WhatsApp
Questões Vunesp – Matemática PDF: Prepare-se com Qualidade
🟡Questões Resolvidas de Matemática em PDF da Banca VUNESP – Nível Fundamental
🔵Questões Resolvidas de Matemática em PDF da Banca VUNESP – Nível Médio
🟠Questões Resolvidas de Matemática em PDF da Banca VUNESP – Nível Superior
Raciocínio Lógico Lista em PDF Vunesp
🟣Raciocínio Lógico – Lista de Exercícios Vunesp (Nível Médio)
🟢Raciocínio Lógico – Lista de Exercícios Vunesp (Nível Superior)
🟢Mapas Mentais de Matemática para Concurso
