Os números naturais são os primeiros conceitos que aprendemos na matemática. Eles surgiram da necessidade de contar objetos e organizar informações. A simplicidade e a aplicação prática dos números naturais os tornam essenciais em diversas áreas do conhecimento.
Definição de Números Naturais
Os números naturais são os números inteiros não-negativos usados para contar e ordenar. São representados pelo conjunto N e são definidos como:
N = {0, 1, 2, 3, 4, 5, 6, 7, }
Em algumas definições, o número 0 não é considerado um número natural, e o conjunto seria representado como N*, que contém somente os números a partir de 1:
N* = {1, 2, 3, 4, 5, 6, 7, …}
Esses números são infinitos, ou seja, sempre podemos adicionar 1 ao maior número e obter outro número natural.
História dos Números Naturais
A origem dos números naturais remonta às primeiras civilizações, quando as pessoas começaram a sentir a necessidade de contar. Os primeiros registros de números vêm de cerca de 4.000 a.C., com os egípcios e babilônios. Eles usavam símbolos para representar quantidades e desenvolveram sistemas de numeração que eventualmente evoluíram para o que usamos hoje.
Ao longo do tempo, os números naturais se tornaram a base da aritmética, sendo amplamente utilizados para representar quantidades e realizar operações como adição, subtração, multiplicação e divisão.
Propriedades dos Números Naturais
Os números naturais possuem diversas propriedades importantes:
1. Infinidade
O conjunto dos números naturais é infinito. Não importa quão grande seja um número natural, sempre podemos adicionar 1 e obter outro número natural maior.
2. Ordenação
Os números naturais estão dispostos em ordem crescente. Isso significa que, se tivermos dois números naturais ( a ) e ( b ), com ( a < b ), então ( b ) é maior que ( a ).
3. Paridade
Os números naturais podem ser classificados como pares ou ímpares:
- Números pares: São divisíveis por 2, como 0, 2, 4, 6, 8, etc.
- Números ímpares: Não são divisíveis por 2, como 1, 3, 5, 7, 9, etc.
4. Fechamento
O conjunto dos números naturais é fechado sob as operações de adição e multiplicação. Isso significa que a soma ou o produto de dois números naturais sempre resulta em outro número natural.
- Exemplo de soma: ( 3 + 5 = 8 )
- Exemplo de multiplicação: ( 4 x 6 = 24 )
Contudo, o mesmo não ocorre para a subtração e a divisão, pois a subtração pode resultar em números negativos, e a divisão pode não ser exata:
- Exemplo de subtração: ( 5 – 7 = -2 ) (que não é um número natural)
- Exemplo de divisão: ( 5 / 2 = 2,5 ) (que também não é um número natural)
Operações com Números Naturais
1. Adição
A adição é a operação mais simples com números naturais, e pode ser entendida como a união de conjuntos disjuntos.
- Exemplo: ( 3 + 4 = 7 )
2. Subtração
A subtração de dois números naturais só resulta em outro número natural se o primeiro número for maior ou igual ao segundo.
- Exemplo: ( 8 – 3 = 5 )
3. Multiplicação
A multiplicação pode ser vista como uma soma repetida de um número natural.
- Exemplo: ( 3 x 4 = 12 ) (que é o mesmo que ( 3 + 3 + 3 + 3 ))
4. Divisão
A divisão entre dois números naturais nem sempre resulta em outro número natural, exceto quando o divisor é um divisor exato do dividendo.
- Exemplo: ( 12 / 4 = 3 ) (divisão exata)
- Exemplo: ( 7 / 2 = 3,5 ) (não é um número natural)
Relação com Outros Conjuntos Numéricos
Os números naturais são a base para outros conjuntos numéricos, como os inteiros Z, os racionais Q, e os reais R. Cada um desses conjuntos expande os números naturais para incluir novos elementos:
- Os inteiros Z incluem os números negativos: {… ,−3 ,−2, −1, 0, 1, 2, 3, …}.
- Os racionais Q incluem frações: a/b com a, b ∈ Z e b ≠ 0.
- Os reais R incluem números com parte decimal, como √2 e π.
Importância dos Números Naturais
Os números naturais são fundamentais para a matemática e suas aplicações. Usamos números naturais para contar, medir, organizar e resolver problemas do cotidiano. Desde contagem de dinheiro até a classificação de dados, os números naturais estão presentes em quase todas as atividades humanas.
Na matemática avançada, os números naturais desempenham um papel crucial em áreas como a teoria dos números, combinatória, álgebra e análise.
Exemplos e Aplicações
Os números naturais são utilizados em diversas situações práticas, como:
- Contagem de objetos: Quantos alunos há na sala? (Resposta: 25, um número natural)
- Medidas de tempo: Quantos dias há no mês? (Resposta: 30, um número natural)
- Classificação de dados: Quantas vendas foram realizadas hoje? (Resposta: 50, um número natural)
Conclusão
Os números naturais são o ponto de partida para o desenvolvimento da matemática. Embora simples, eles são essenciais para a contagem, organização e solução de problemas. Desde sua origem em antigas civilizações até seu uso moderno, os números naturais formam a base de muitos dos conceitos matemáticos que usamos diariamente.
Através de suas propriedades e operações, os números naturais continuam a ser um campo de estudo fundamental e uma ferramenta valiosa para compreender o mundo ao nosso redor.
Exercício Prático
Resolva os seguintes problemas sobre números naturais:
- Qual é a soma dos seis primeiros números naturais?
- O produto dos três primeiros números naturais pares é quanto?
- Qual é o maior número natural entre 0 e 10?
Esses exercícios ajudam a reforçar o entendimento sobre números naturais e suas aplicações.
Conjuntos Numéricos: Exercícios com Soluções Detalhadas
Números Naturais: Lista de Exercícios com Soluções Detalhadas
Exercício 01 – Responda às perguntas.
a) 15 e XV representam quantidades diferentes?
b) 15 e XV são numerais diferentes?
Ver Solução

Exercício 02 – Sobre o número 478 194 235, responda:
a) Que algarismo ocupa a posição da centena de milhar?
b) Em que ordem está o algarismo 7?
c) Esse número é múltiplo de 2, de 3 ou de 5?
Ver Solução

Exercício 03 – Sobre os números naturais de 1 a 1 000,
responda:
a) Quantos têm o algarismo 5 na ordem das dezenas?
b) Quantos têm o algarismo 5 na ordem das unidades?
Ver Solução


Exercício 04 – Responda:
a) Quais são e como são chamados os números naturais múltiplos de 2?
b) Quais são os dez primeiros números naturais ímpares?
Ver Solução
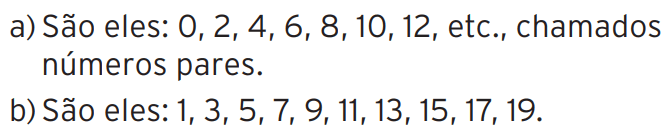
Exercício 05 – Responda:
a) O que é um número natural primo?
b) Quais são os dez primeiros números naturais primos?
Ver Solução

Exercício 06 – Sobre o número 2 020, responda:
a) Sem considerar a ordem dos fatores, de quantos modos podemos obter o resultado 2 020 multiplicando dois números naturais?
b) E multiplicando três números naturais?
Ver Solução

Exercício 07 – Considerando que dois números naturais são equivalentes se a soma dos divisores de um deles coincide com a soma dos divisores do outro, responda:
a) Os números 6 e 9 são equivalentes?
b) Os números 16 e 25 são equivalentes?
c) Existe algum número natural equivalente a 10? Qual?
Ver Solução

Exercício 08 – O que são dois números primos entre si? Dê um exemplo.
Ver Solução
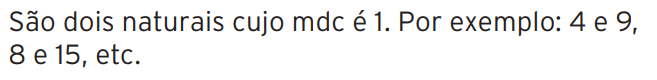
Exercício 09 – Sabemos que um número natural é divisível por 6 quando é divisível por 2 e por 3. Isso ocorre porque 2 e 3 são números primos entre si e 6 5 2 3.
a) Como podemos saber se um número natural é divisível por 12, sem efetuar a divisão?
b) E por 15?
c) Dos números da lista abaixo quais são divisíveis por 12? E por 15?

Ver Solução

Exercício 10 – Quantos são os múltiplos de 4 que possuem apenas dois algarismos?
Ver Solução

Exercício 11 – Considere a sucessão numérica abaixo.
7, 14, 21, 28, 35, 42, ….
Qual é o último número dessa sucessão que podemos representar com três algarismos?
Ver Solução

Exercício 12 – Na sequência de Fibonacci os dois primeiros números são 1 e 1. A partir daí, cada número é igual à soma dos dois anteriores:
1, 1, 2, 3, 5, 8, 13, 21, …
Qual é o primeiro número dessa sequência que se escreve com três algarismos?
Ver Solução

Exercício 13 – Na sequência numérica (2, 3,__ ,__ ,__ ,__ , …) a soma de três termos sucessivos é sempre igual a 10. Responda:
a) Quais são os números que estão representados por “__” na sequência?
b) Qual é o centésimo número dessa sequência?
c) Qual é a soma dos 100 primeiros números dessa sequência?
Ver Solução

Exercício 14 – Veja as duas sequências de números figurados a seguir.

Determine:
a) o próximo número de cada sequência;
b) o maior número com dois algarismos de cada sequência.
Ver Solução

Exercício 15 – Decomponha os números abaixo em fatores primos:
a) 150
b) 1502
c) 500
d) 5002
Ver Solução
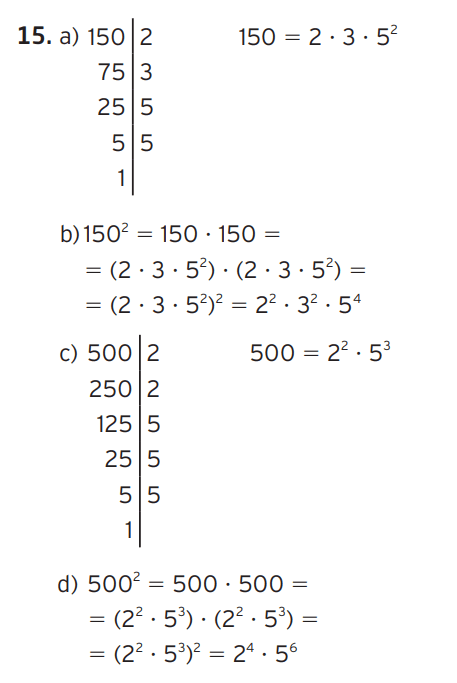
Exercício 16 – Responda se a afirmação é verdadeira ou falsa:
“Sendo p um número natural maior que 1, na decomposição de p2 em fatores primos, todos os expoentes são números pares”.
Ver Solução

Exercício 17 – Dado o número p = 160, quantas vezes o número 2 aparece na de com posição em fatores primos de:
a) p
b) p2
c) 2 x p2
Ver Solução
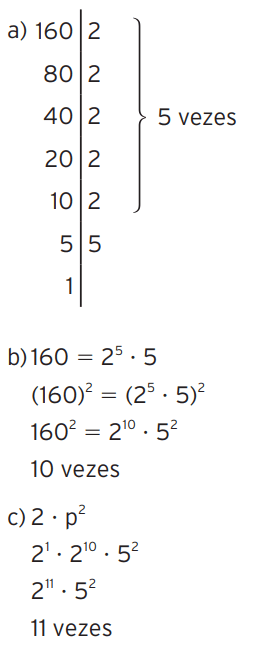
Exercício 18 – Sendo p um número inteiro maior que 1, na decomposição em fatores primos do número p2 o expoente do fator primo 2 é par ou ímpar? E na decomposição do número 2p2?
Ver Solução













