Introdução
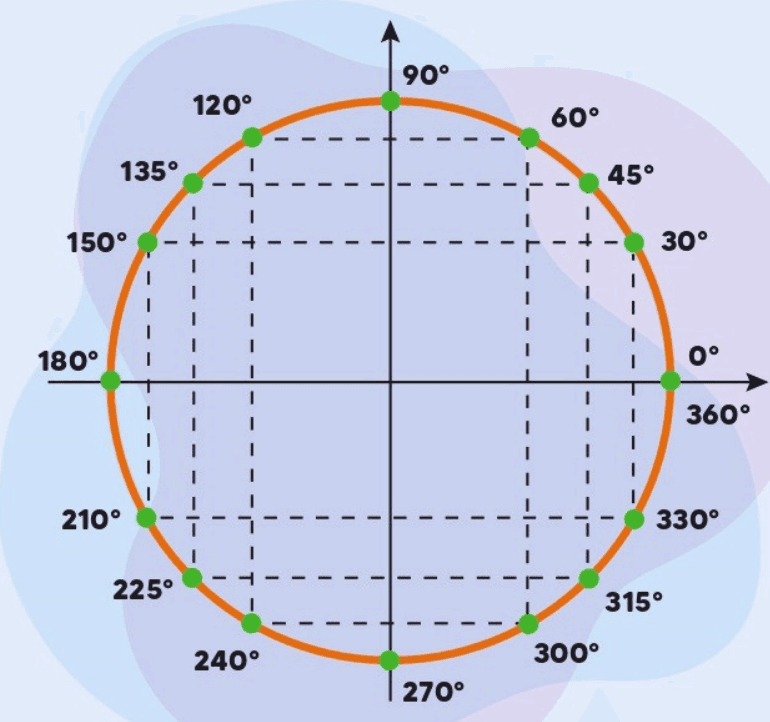
Na matemática, o círculo trigonométrico, também conhecido como círculo unitário ou círculo goniométrico, é uma ferramenta fundamental em trigonometria. Este círculo, com raio igual a um, é centrado na origem do plano cartesiano e serve como uma base para definir funções trigonométricas como seno, cosseno e tangente. Além disso, ele é essencial para a compreensão de conceitos como ângulos, radianos, e suas relações no plano cartesiano.
Definição e Propriedades
O círculo trigonométrico é definido como um círculo de raio unitário, ou seja, um círculo com raio r = 1, centrado na origem do plano cartesiano, com equação dada por:
x2 + y2 = 1
Neste contexto, qualquer ponto P(x, y) no círculo trigonométrico pode ser associado a um ângulo θ medido a partir do eixo positivo x, onde x é o cosseno do ângulo cosθ e y é o seno do ângulo sinθ:
P(cosθ, sinθ)
Esses valores de x e y variam entre -1 e 1, dependendo do quadrante no qual o ponto P se encontra.
Funções Trigonométricas
As funções trigonométricas seno, cosseno e tangente são definidas diretamente a partir do círculo trigonométrico. Para um dado ângulo ( \theta ), as seguintes relações são válidas:
- Seno (sin θ): Representa a coordenada ( y ) do ponto ( P ).
- Cosseno (cosθ): Representa a coordenada ( x ) do ponto ( P ).
- Tangente (tanθ): É a razão entre seno e cosseno, ou seja, (tanθ = sinθ/cosθ), definida em todos os pontos onde ( cosθ ≠ 0 ).
Essas funções são fundamentais para a resolução de problemas que envolvem ângulos e distâncias em diversas áreas da ciência e engenharia.
Ângulos e Radianos
Outra aplicação importante do círculo trigonométrico é a conversão entre graus e radianos. O comprimento de um arco de círculo unitário corresponde diretamente ao valor do ângulo em radianos, onde ( 2\pi ) radianos correspondem a ( 360^\circ ). Isso significa que um radiano é equivalente ao ângulo subtendido por um arco cujo comprimento é igual ao raio do círculo (neste caso, 1).
- Conversão de Graus para Radianos:
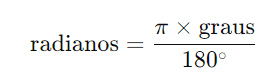
- Conversão de Radianos para Graus:

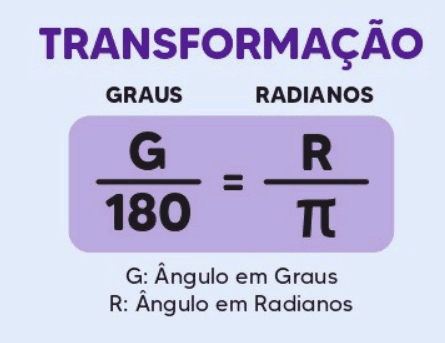

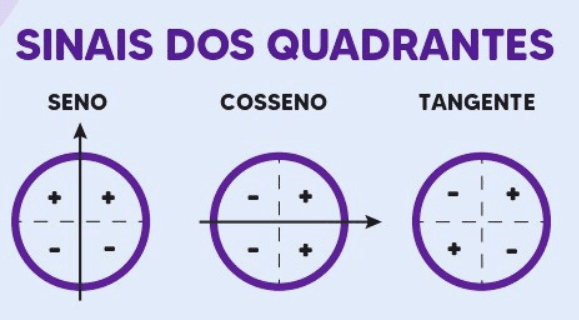
Aplicações e Importância
O círculo trigonométrico é amplamente utilizado em diversas áreas, desde a física até a engenharia, passando pela computação gráfica e a análise de sinais. Ele permite a visualização e compreensão das funções trigonométricas de maneira intuitiva e geométrica, facilitando a resolução de equações trigonométricas e a análise de fenômenos periódicos.
Além disso, a generalização do círculo trigonométrico para dimensões superiores leva ao conceito de esfera unitária, fundamental em cálculos envolvendo vetores e coordenadas esféricas em três dimensões.
Conclusão
O círculo trigonométrico é uma ferramenta essencial na matemática e em várias ciências aplicadas. Sua simplicidade e versatilidade permitem uma compreensão profunda das relações trigonométricas e suas aplicações práticas. Ao dominar o conceito do círculo trigonométrico, ganha-se uma base sólida para explorar muitos outros tópicos avançados na matemática e nas ciências exatas.

























