A permutação circular é um conceito da análise combinatória que aborda a organização de elementos em forma de círculo, como em uma mesa redonda ou em um anel de chaveiros. Diferente da permutação linear, onde o início e o fim são fixos, a permutação circular leva em conta que as posições dos elementos são relativas, ou seja, girar o círculo não cria uma nova permutação.
Neste artigo, exploraremos o que é permutação circular, apresentaremos a fórmula, explicaremos como aplicá-la e resolveremos exercícios práticos. Se você deseja dominar esse conceito de matemática, este guia é para você.

Transforme seus estudos com o eBook Matemática Resumida: + de 90 Mapas Mentais de Matemática! Simplifique conceitos complexos, organize seus estudos e revise de forma prática e eficiente. Baixe agora e conquiste seus objetivos!
O Que é Permutação Circular?
A permutação circular é usada para calcular o número de maneiras de organizar elementos em forma de círculo, onde as posições dos elementos dependem de sua relação com os outros e não de um ponto fixo.
Por exemplo:
- Se temos 3 pessoas (A, B e C) sentadas em uma fila, as permutações são: ABC, ACB, BAC, BCA, CAB, CBA (6 possibilidades).
- Em uma mesa redonda, as permutações seriam reduzidas porque girar a mesa não altera a relação entre as pessoas. Nesse caso, só existem 2 permutações únicas.
Fórmula da Permutação Circular
A fórmula para calcular a permutação circular de n elementos é:
Pc = (n − 1)!
Aqui, subtraímos 1 do total de elementos porque uma posição é considerada fixa para evitar redundâncias devido à rotação.
Exemplo do Uso da Fórmula:
Quantas maneiras diferentes 5 pessoas podem se sentar ao redor de uma mesa redonda?
Solução:
- Total de pessoas (n): 5.
- Aplicando a fórmula:
Pc = (5 − 1)! = 4! = 4×3×2×1 = 24
Portanto, há 24 maneiras únicas de organizar as pessoas.
📚 Quer aprofundar seus conhecimentos em Análise Combinatória e Probabilidade? Confira nossa recomendação dos melhores livros sobre o tema com exercícios resolvidos e dicas práticas. 👉Os melhores livros de Analise Combinatória e Probabilidade
Diferença Entre Permutação Linear e Circular
| Tipo | Descrição | Fórmula |
|---|---|---|
| Permutação Linear | Organização em linha reta, onde a ordem importa. | P(n) = n! |
| Permutação Circular | Organização em círculo, onde as posições são relativas. | Pc = (n – 1)! |
Casos Especiais da Permutação Circular
1. Permutação Circular com Repetição
Se houver elementos repetidos, usamos a fórmula ajustada para considerar as repetições:
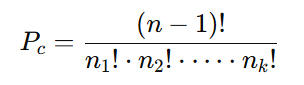
- n: total de elementos.
- n1, n2, …, nk: número de repetições de cada elemento.
Exemplo Prático:
1 – Um colar é formado por 7 pérolas, sendo 4 brancas e 3 pretas. Quantas combinações distintas podem ser feitas ao organizar essas pérolas em forma de círculo?
Solução:
Identifique o total de elementos e as repetições:
- Total de pérolas (n): 7.
- Pérolas brancas (n1): 4.
- Pérolas pretas (n2): 3.
Aplicando a fórmula:
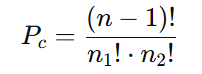
Substituindo os valores:
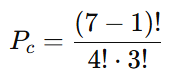
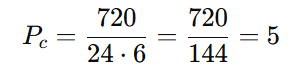
Existem 5 combinações distintas de organizar as pérolas no colar circular, considerando as repetições.
2 – Temos 3 bolas pretas (P) e 2 bolas brancas (B). Quantos modos distintos podemos organizá-las em um círculo?
Identifique o número total de elementos e as repetições:
- Total de bolas (n): 5.
- Bolas pretas (n1): 3.
- Bolas brancas (n2): 2.
Entenda o conceito de permutação circular com repetição: Como as bolas são organizadas em um círculo, girar o arranjo não cria uma nova permutação distinta. Além disso, as bolas pretas e brancas são idênticas dentro de seus grupos, o que reduz ainda mais o número de combinações únicas.
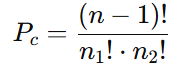
Substituímos os valores:
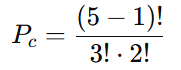
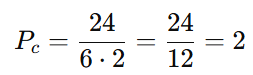
Existem 2 modos distintos de organizar as 3 bolas pretas e 2 bolas brancas em um círculo.
👉Entre no nosso canal do WhatsApp
📘 Todas as fórmulas de matemática em um só lugar! Baixe agora nosso eBook gratuito
Exercícios Resolvidos
Exercício 1: Mesa Redonda
Quantas maneiras diferentes podemos organizar 6 pessoas ao redor de uma mesa redonda?
Solução:
- Total de pessoas (n): 6.
- Aplicando a fórmula:
Pc = (n − 1)! = (6 − 1)! = 5! = 5×4×3×2×1 = 120
Resposta: Existem 120 maneiras de organizar as 6 pessoas.
Exercício 2: Jóias em um Colar
Um colar tem 5 pérolas, todas diferentes. Quantas combinações únicas podem ser feitas?
Solução:
Aqui, o colar pode ser girado e também invertido (virado do avesso), reduzindo o total de permutações pela metade.
Fórmula ajustada:
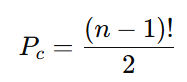
Aplicando a fórmula:
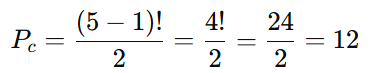
Resposta: Existem 12 combinações únicas.
Aplicações da Permutação Circular
A permutação circular é muito usada em problemas práticos e acadêmicos, especialmente na matemática e na análise combinatória. Aqui estão algumas aplicações:
- Organização de Eventos:
Planejar a disposição de pessoas ao redor de uma mesa ou palco. - Design e Moda:
Criar padrões únicos para colares, pulseiras ou ornamentos circulares. - Jogos e Competições:
Determinar posições de jogadores em torneios circulares. - Arquitetura e Design de Interiores:
Planejar a disposição de móveis em espaços circulares, como mesas redondas ou praças.
Resumo
A permutação circular é uma variação fascinante da análise combinatória, essencial para resolver problemas onde os elementos são dispostos em círculos. Ao contrário da permutação linear, ela considera que girar o círculo não cria novas combinações. Sua fórmula, Pc=(n−1)!, é simples de aplicar e se ajusta facilmente para lidar com repetições.
Agora que você domina o conceito, que tal resolver mais problemas e explorar ainda mais as aplicações desse tema? A prática é essencial para dominar a matemática e se destacar em suas análises combinatórias!