Prepare-se para o concurso dos Correios com 10 questões de matemática essenciais para sua revisão. Este conteúdo foi elaborado para testar e aprimorar seus conhecimentos, cobrindo tópicos importantes que podem cair na prova. Confira as resoluções e dicas práticas para garantir um bom desempenho no dia do exame!
01 – Equação Exponencial – Concurso Correios 2008 – Banca CONSULPLAN
A raiz da equação
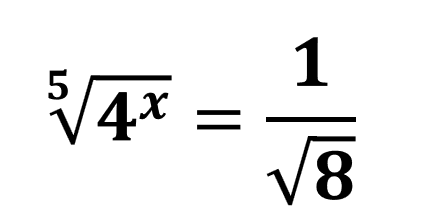
é um número:
A) irracional negativo.
B) natural.
C) racional negativo.
D) inteiro.
E) equivalente a – 15,4.
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
A solução para a equação dada na imagem é a seguinte:
Equação:
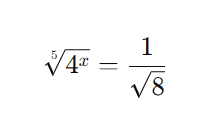
Passo 1: Simplificação das bases
Sabemos que ( 4 = 22 ) e ( 8 = 23 ), então podemos reescrever a equação como:
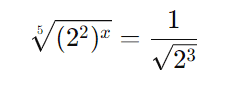
Passo 2: Aplicação das propriedades de potências
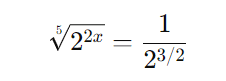
A equação agora fica:
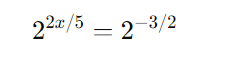
Passo 3: Igualação dos expoentes
Como as bases são iguais, podemos igualar os expoentes:
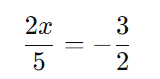
Passo 4: Resolução da equação
Multiplicamos ambos os lados por 5 para eliminar o denominador da esquerda:
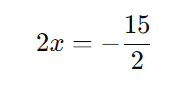
Agora, dividimos ambos os lados por 2:
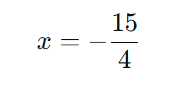
Resposta:
A raiz da equação é um número racional nega
[/toggle]
02 – Equação do 1° Grau – Concurso Correios 2008 – Banca CONSULPLAN
Seis pessoas trabalham na casa do Sr. Silva: uma cozinheira, duas copeiras, duas faxineiras e um jardineiro. Para pagar seus funcionários, Sr. Silva gasta R$3.134,00. As pessoas que trabalham em funções iguais, ganham salários iguais. O salário mensal da cozinheira é de R$260,00 a mais que o salário de uma faxineira. Uma copeira ganha tanto quanto ganha um jardineiro e este, ganha R$200,00 a menos que uma faxineira. Qual é o salário da cozinheira?
A) R$654,80
B) R$839,00
C) R$1.418,00
D) R$579,00
E) R$914,80
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
Vamos organizar as informações para montar um sistema de equações e resolver o problema.
Definindo as variáveis:
- Seja S o salário de uma faxineira.
- O jardineiro e as copeiras ganham o mesmo salário, que é S − 200.
- A cozinheira ganha S + 260
Total de salários:
O Sr. Silva paga um total de R$3.134,00, e temos:
- 1 cozinheira ganhando S+260,
- 2 copeiras ganhando S−200,
- 2 faxineiras ganhando S cada,
- 1 jardineiro ganhando S−200.
Montando a equação total:
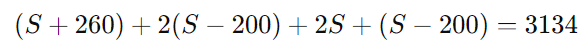
Simplificando a equação:
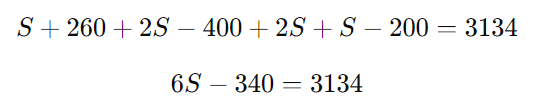
Somando 340 dos dois lados:
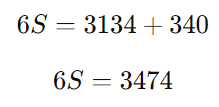
Dividindo ambos os lados por 6:
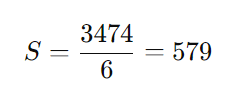
O salário de uma faxineira é S=579.
Agora, o salário da cozinheira é S+260:
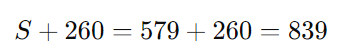
Portanto, o salário da cozinheira é R$ 839,00.
A resposta correta é:
B) R$839,00.
[/toggle]
03 – Estatística – Concurso Correios 2008 – Banca CONSULPLAN
Uma pesquisa realizada em 2004 obteve os seguintes resultados sobre os e-mails indesejáveis mais comuns:
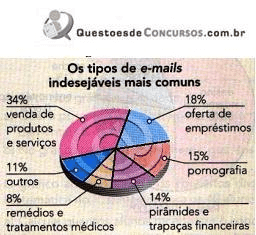
Se uma pessoa recebeu 31 e-mails sobre venda de produtos e serviços em uma semana, isso significa que essa pessoa recebeu aproximadamente quantos e-mails por semana?
A) 91
B) 105
C) 109
D) 95
E) 104
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
A imagem mostra uma pesquisa sobre os tipos de e-mails indesejáveis mais comuns, com os seguintes percentuais:
- 34% para venda de produtos e serviços,
- 18% para oferta de empréstimos,
- 15% para pornografia,
- 14% para pirâmides e trapaças financeiras,
- 8% para remédios e tratamentos médicos,
- 11% para outros.
Sabemos que a pessoa recebeu 31 e-mails sobre venda de produtos e serviços em uma semana, o que corresponde a 34% do total de e-mails recebidos. Para descobrir o total de e-mails, vamos montar uma regra de três simples.
Seja ( x ) o total de e-mails recebidos na semana. Temos a relação:

Escrevendo isso matematicamente:
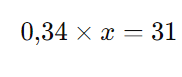
Agora, isolamos ( x ):
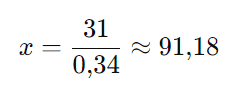
Portanto, a pessoa recebeu aproximadamente 91 e-mails por semana.
A resposta correta é:
A) 91.
[/toggle]
04 – Função Afim- Concurso Correios 2008 – Banca CONSULPLAN
Ricardo usa a Internet em horários e dias em que é cobrada uma taxa única a cada vez que faz uma conexão. Assim, gasta mensalmente R$25,00 com o provedor e mais R$3,00 por acesso (conexão). No último mês, conectou a Internet várias vezes e pagou R$85,00. Se esse mês ele conectar o dobro de vezes do mês passado, quanto ele pagará?
A) R$180,00
B) R$170,00
C) R$145,00
D) R$120,00
E) R$154,00
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
Vamos resolver o problema passo a passo:
- Definir as variáveis:
- O valor mensal fixo que Ricardo paga ao provedor é de R$25,00.
- Ele paga R$3,00 por cada acesso (conexão) à Internet.
- No mês passado, ele pagou um total de R$85,00.
Montar a equação:
Sabemos que o total pago é a soma do valor fixo mensal mais o valor gasto com as conexões. Podemos montar a seguinte equação:
25 + 3x = 85
Onde ( x ) é o número de acessos (conexões) que ele fez no mês passado.
Resolver a equação:
Subtraímos 25 de ambos os lados: [
3x = 85 – 25
3x = 60
Agora, dividimos ambos os lados por 3 para encontrar o valor de ( x ):
x = 60/3 = 20
Então, no mês passado, Ricardo fez 20 conexões.
Dobrar o número de acessos:
Se este mês ele fizer o dobro de acessos, o número de acessos será (2 x 20 = 40 ) conexões.
Calcular o total a pagar neste mês:
O total pago será a soma do valor fixo mensal de R$25,00 mais o valor por 40 acessos, que é ( 40 x 3 = 120 ). Portanto:
Total = 25 + 120 = 145
Resposta: Ele pagará R$145,00 este mês.
A alternativa correta é C) R$145,00.
[/toggle]
05 – Função do Segundo Grau – Concurso Correios 2008 – Banca CONSULPLAN
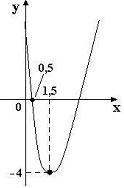
Qual é a lei da função representada pelo gráfico abaixo?
A) y = x² – 2,5x + 5
B) y = í 4x² – 2x + 10
C) y = 4x² – 12x + 5
D) y = 2x² – 12x + 5
E) y = x² – 0,5x + 5
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
Vamos resolver o problema usando as informações fornecidas e montar um sistema de equações para encontrar os coeficientes (a), (b) e (c).
Passo 1: Fórmula geral da função quadrática
Sabemos que a equação da função quadrática tem a forma:
y = ax2 + bx + c
Passo 2: Usando os pontos fornecidos
Temos as seguintes informações:
- O vértice está no ponto (1,5; -4),
- O ponto (0,5; 0) também pertence à parábola.
Além disso, o valor de yv = -4 (valor do vértice).
Passo 3: Montando o sistema de equações
- Primeira equação (vértice ( (1,5, -4) )):
Substituímos x = 1,5 e y = -4 na equação geral:
-4 = a(1,5)2 + b(1,5) + c
-4 = a(2,25) + 1,5b + c
2,25a + 1,5b + c = -4
- Segunda equação ponto (0,5; 0):
Substituímos (x = 0,5) e (y = 0) na equação geral:
0 = a(0,5)2 + b(0,5) + c
0 = a(0,25) + 0,5b + c
0,25a + 0,5b + c = 0
- Terceira Equação: Utilizando xv = 1,5, temos:
xv = -b/2a
1,5= -b/2a
1,5 x 2a= -b
b = -3a
Passo 4: Resolvem o sistema
Agora, temos um sistema com três equações:
Vamos resolver o sistema de equações passo a passo.
Sistema de Equações
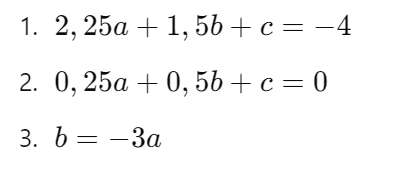
Passo 1: Substituir ( b ) na Equação 1 e 2
Usando a Equação 3 (( b = -3a )), substituímos ( b ) nas equações 1 e 2.

Substituindo na Equação 2:
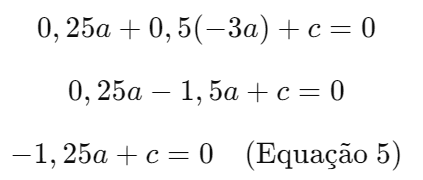
Passo 2: Resolver o Sistema com as Equações 4 e 5
Agora temos um sistema com duas equações e duas incógnitas:
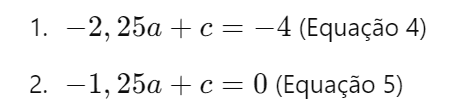
Vamos subtrair a Equação 5 da Equação 4 para eliminar ( c ).
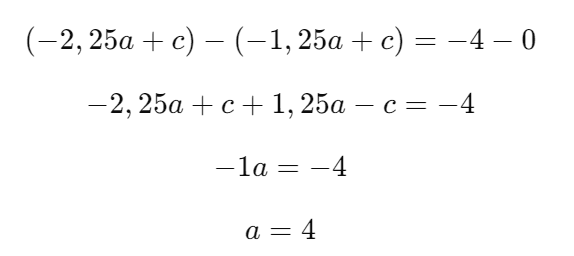
Passo 3: Encontrar ( c )
Substituímos ( a = 4 ) em qualquer uma das Equações 4 ou 5 para encontrar ( c ).
Usando a Equação 5:

Passo 4: Encontrar ( b )
Agora, usamos a Equação 3 para encontrar ( b ).

Solução Final
Os valores encontrados são:
- ( a = 4 )
- ( b = -12 )
- ( c = 5 )
Esses são os valores das variáveis que satisfazem todas as equações do sistema.
Logo y = 4x2 – 12 + 5
[/toggle]
06 – Geometria Espacial – Concurso Correios 2011 – Banca CESPE
Para o envio de pequenas encomendas, os Correios comercializam caixas de papelão, na forma de paralelepípedo retângulo, de dois tipos: tipo 2, com arestas medindo 27 cm, 18 cm, e 9 cm; e tipo 4, com arestas medindo 36 cm, 27 cm e 18 cm.
Se um escritor deseja enviar livros de sua autoria a outro estado e se cada livro mede 23 cm × 16 cm × 1,2 cm, então a quantidade máxima desses livros que poderá ser enviada em uma caixa do tipo 2, sem que sejam danificados ou deformados, é igual a
A) 9
B) 5
C) 6
D) 7
E) 8
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
Para resolver o problema, devemos calcular quantos livros cabem dentro de uma caixa do tipo 2, levando em conta o volume da caixa e o volume de cada livro, além de verificar a disposição possível dos livros dentro da caixa.
Dimensões:
- Caixa tipo 2: 27 cm × 18 cm × 9 cm
- Livro: 23 cm × 16 cm × 1,2 cm
Etapas:
1. Verificar as possíveis orientações para o posicionamento dos livros na caixa:
Temos que testar as combinações das dimensões do livro e da caixa para ver quantos livros cabem em cada direção.
Tentativa 1:
Colocando o comprimento do livro (23 cm) ao longo do comprimento da caixa (27 cm):

Neste arranjo, cabem no máximo 7 livros.
[/toggle]
07 – Geometria Plana – Concurso Correios 2011 – Banca CESPE
Se o perímetro de um terreno em forma de retângulo é igual a 180 m e se um dos lados desse retângulo mede 10 m a mais que o outro, então a área do terreno é igual a
A) 1.800 m2 .
B) 1.600 m2 .
C) 1.400 m2 .
D) 1.200 m2 .
E) 2.000 m2 .
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
Vamos resolver a questão utilizando ( x ) e ( x + 10 ) como os lados do retângulo:
- O perímetro de um retângulo é dado por:
P = 2 x (L + l)
- Sabemos que o perímetro do terreno é 180 metros. Se um lado é x e o outro é x + 10, então temos:
180 = 2 x(x + (x + 10))
- Simplificando a equação:
180 = 2 x (2x + 10)
Dividindo ambos os lados por 2:
90 = 2x + 10
Subtraindo 10 de ambos os lados:
80 = 2x
Dividindo por 2:
x = 40
- Agora, substituímos o valor de ( x ):
- O lado menor é ( x = 40 ).
- O lado maior é ( x + 10 = 40 + 10 = 50 ).
- Agora podemos calcular a área do retângulo:
A = x x (x + 10) = 40 x 50 = 2.000 m2
Portanto, a área do terreno é 2.000 m².
A resposta correta é E) 2.000 m².
[/toggle]
08 – Inequação do Segundo Grau – Concurso Correios 2008 – Banca CONSULPLAN
Determine o valor de m de modo que o trinômio (m – 2) x² – (m – 1) x + m – 1 seja sempre positivo:
A) m = 7/3
B) m = 1
C) m < 7/3
D) m < 1
E) m > 2(1/3)
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
Vamos resolver essa questão para encontrar o valor de m de modo que o trinômio (m – 2)x2 – (m – 1)x + (m – 1) seja sempre positivo utilizando os conhecimentos das inequações do 2° grau.
Para que um trinômio quadrático ( ax2 + bx + c ) seja sempre positivo, é necessário que:
- O coeficiente de ( x2 ) seja positivo, ou seja, ( a > 0 ).
- O discriminante ( ∆ ) da equação quadrática seja negativo, ou seja, ( ∆ < 0 ), para que não haja raízes reais.
Passo 1: Identificar os coeficientes do trinômio
Comparando (m – 2)x2 – (m – 1)x + (m – 1) com a equação geral ( ax2 + bx + c ), temos:
- a = m – 2
- b = -(m – 1)
- c = m – 1
Passo 2: Garantir que ( a > 0 )
Para que o trinômio seja sempre positivo, o coeficiente de ( x2 ), que é ( m – 2 ), deve ser positivo:
m – 2 > 0
m > 2
Passo 3: Calcular o discriminante e garantir que ( ∆ < 0 )
O discriminante ( \Delta ) da equação quadrática é dado por:
∆ = b^2 – 4ac
Substituindo os valores de ( a ), ( b ), e ( c ):
∆ = (-(m – 1))2 – 4(m – 2)(m – 1)
Calculando:
∆ = (m – 1)2 – 4(m – 2)(m – 1)
Expandindo os termos:
∆ = (m2 – 2m + 1) – 4(m2 – 3m + 2)
∆ = m2 – 2m + 1 – 4(m2) + 12m – 8
∆ = m2 – 2m + 1 – 4m2 + 12m – 8
Simplificando:
∆ = -3m2 + 10m – 7
Para que não haja raízes reais, é necessário que ( ∆ < 0 ):
-3m2 + 10m – 7 < 0
Multiplicando a equação por ( -1 ) (lembrando que isso inverte o sinal da desigualdade):
3m2 – 10m + 7 > 0
Agora, precisamos resolver a equação quadrática ( 3m2 – 10m + 7 = 0 ) para encontrar as raízes.
Passo 4: Encontrar as raízes da equação
Usamos a fórmula de Bhaskara:
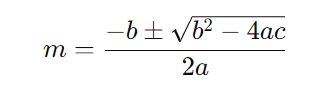
Com ( a = 3 ), ( b = -10 ), e ( c = 7 ):
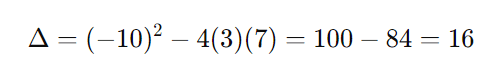
As raízes são:
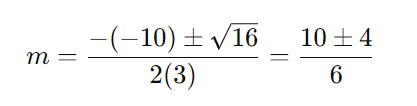
As duas soluções são:
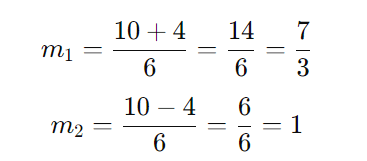
Passo 5: Analisar o sinal da equação
A inequação ( 3m2 – 10m + 7 > 0 ) é satisfeita para valores de ( m ) fora do intervalo entre as raízes ( 7/3) e ( 1 ). Portanto, a solução é:
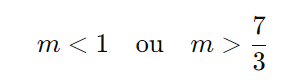
Passo 6: Verificar as opções
A alternativa correta que garante que o trinômio seja sempre positivo é m > 7/3.
A resposta correta é E) m > 2(1/3).
[/toggle]
09 – Logaritmo – Concurso Correios 2008 – Banca CONSULPLAN
A equação n(t) = 20 + 15log125(t + 5) representa uma estimativa sobre o número de funcionários de uma Agência dos Correios de uma certa cidade, em função de seu tempo de vida, em que n(t) é o número de funcionários no t- enésimo ano de existência dessa empresa(t = 0, 1, 2…). Quantos funcionários essa Agência possuía quando foi fundada?
A) 105
B) 11
C) 45
D) 65
E) 25
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
Para encontrar o número de funcionários quando a Agência dos Correios foi fundada, precisamos calcular n(t) para ( t = 0 ) na Função Logarítmica.
Substituindo ( t = 0 ) na equação:
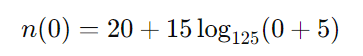
Simplificando:
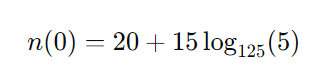
Agora, podemos usar a mudança de base para calcular ( log125(5) ). Lembre-se que ( 125 = 53 ), então:
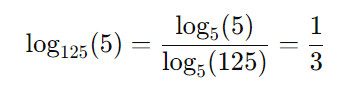
Substituindo isso na equação:
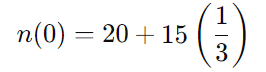
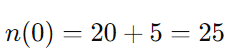
Portanto, a Agência dos Correios possuía 25 funcionários quando foi fundada. A resposta correta é:
E) 25.
[/toggle]
10 – Matemática Básica – Concurso Correios 2008 – Banca CONSULPLAN
Três irmãos A, B, C matricularam-se numa escola de informática que adota a seguinte política de preços: a mensalidade dos quatro primeiros meses é de R$90,00 e a partir daí, há um desconto de R$15,00 no valor da mensalidade (limitado a 8 meses). Qual foi o valor pago pelos três irmãos, sabendo que A estudou durante 4 meses, B durante 9 meses e C durante 12 meses?
A) R$1.380,00
B) R$1.935,00
C) R$2.055,00
D) R$1.875,00
E) R$2.010,00
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
Vamos calcular o valor pago por cada irmão separadamente, considerando a política de preços da escola.
1. Irmão A (estudou durante 4 meses)
A mensalidade para os quatro primeiros meses é de R$90,00. Como o irmão A estudou apenas 4 meses, ele pagou:
Total de A = 4 x 90 = R$360,00
2. Irmão B (estudou durante 9 meses)
Os quatro primeiros meses têm mensalidade de R$90,00. A partir do 5º mês, há um desconto de R$15,00, ou seja, a mensalidade passa a ser R$75,00. Portanto, o irmão B pagou:
- Para os primeiros 4 meses:
4 x 90 = R$360,00 - Para os próximos 5 meses (com o desconto):
5 x 75 = R$375,00
O total pago por B foi:
Total de B = 360 + 375 = R$735,00
3. Irmão C (estudou durante 12 meses)
Os quatro primeiros meses têm mensalidade de R$90,00, e a partir do 5º mês, a mensalidade passa a ser de R$75,00. Como o irmão C estudou por 12 meses, ele pagou:
- Para os primeiros 4 meses:
4 x 90 = R$360,00 - Para os próximos 8 meses (com o desconto):
8 x 75 = R$600,00
O total pago por C foi:
Total de C = 360 + 600 = R$960,00
Valor total pago pelos três irmãos:
Somando o valor pago por A, B e C:
Total geral = 360 + 735 + 960 = R$2.055,00
Portanto, o valor total pago pelos três irmãos foi R$2.055,00.
A resposta correta é a letra C).
[/toggle]

























