A probabilidade condicional é um conceito fundamental na teoria das probabilidades, dentro da matemática, permitindo calcular a chance de um evento ocorrer com base no conhecimento prévio de que outro evento já aconteceu. Isso é especialmente útil em situações onde o espaço amostral original precisa ser “reduzido” para levar em conta as condições dadas.
Neste artigo, exploraremos o conceito de probabilidade condicional, sua fórmula, e exemplos detalhados para ilustrar diferentes aplicações práticas.

O Que é Probabilidade Condicional?
A probabilidade condicional de A, dado que B ocorreu, é representada como P(A|B). Ela é definida como:
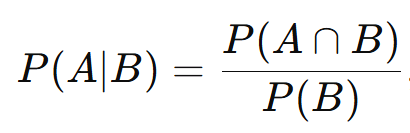
com P(B) > 0
Aqui:
- P(A∩B): Probabilidade de A e B ocorrerem simultaneamente.
- P(B): Probabilidade de B ocorrer.
Por Que Usar Probabilidade Condicional?
Quando sabemos que um evento B já ocorreu, o espaço amostral original (S) é reduzido ao subconjunto onde B é verdadeiro. Assim, a probabilidade de A passa a ser calculada dentro desse espaço reduzido.
Exemplo 1: Escolha Aleatória em um Conjunto de Números
Situação:
Considere o conjunto de números S = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}.
- Evento A: O número escolhido é múltiplo de 3. A = {3, 6, 9}
- Evento B: O número escolhido é maior que 5. B = {6, 7, 8, 9, 10}
Cálculo de P(A|B):
O espaço amostral é reduzido ao conjunto B. No novo espaço:
- B = {6, 7, 8, 9, 10}, com |B| = 5.
- A∩B = {6, 9}, com |A∩B| = 2.
A probabilidade condicional é:

Interpretação:
A probabilidade de o número escolhido ser múltiplo de 3, dado que é maior que 5, é 2/5, ou 40%.
Exemplo 2: Pesquisa Sobre Hábitos de Consumo
Situação:
Uma pesquisa com 1.000 pessoas registrou os hábitos de consumo de café e chá:
| Bebida | Consomem Café (C) | Não Consomem Café (CC) | Total |
|---|---|---|---|
| Consomem Chá (T) | 300 | 100 | 400 |
| Não Consomem Chá (TC) | 400 | 200 | 600 |
| Total | 700 | 300 | 1.000 |
Evento 1: P(T|C)
Qual é a probabilidade de uma pessoa consumir chá, dado que ela consome café?
Solução:
O novo espaço amostral é o conjunto das pessoas que consomem café (C), com |C| = 700.
Entre essas, 300 consomem chá (T∩C).
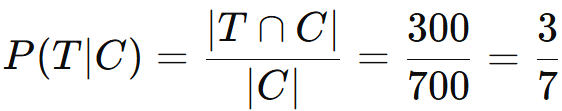
📊 Estude Probabilidade
Aprenda definições, fórmulas e exercícios resolvidos de Probabilidade. Conteúdo direto, ideal para ENEM, vestibulares e concursos.
👉 Acessar o artigo de ProbabilidadeInterpretação:
A probabilidade de uma pessoa consumir chá, dado que consome café, é 3/7, ou aproximadamente 42,86%.
Evento 2: P(C|T)
Qual é a probabilidade de uma pessoa consumir café, dado que ela consome chá?
Solução:
O novo espaço amostral é o conjunto das pessoas que consomem chá (T), com |T| = 400.
Entre essas, 300 consomem café (T∩C).
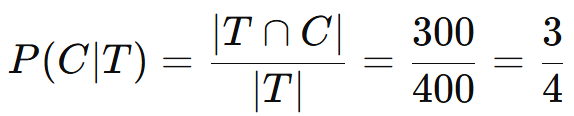
Interpretação:
A probabilidade de uma pessoa consumir café, dado que consome chá, é 3/4, ou 75%.
Exemplo 3: Escolha Aleatória em um Baralho
Situação:
Considere um baralho padrão de 52 cartas.
- Evento A: A carta é uma dama. A={Qc, Qo, Qe, Qp}, |A| = 4
- Evento B: A carta é vermelha. B={copas, ouros}, |B| = 26
Cálculo de P(A|B):
O espaço amostral é reduzido ao conjunto das cartas vermelhas (B). No novo espaço:
- B={2c, 3c, …, Ac, 2o, 3o, …, Ao}, |B| = 26.
- A∩B = {Qc, Qo}, ∣A∩B∣ = 2
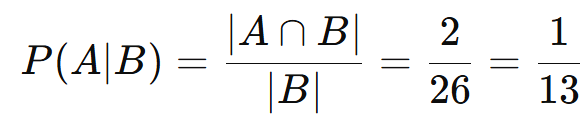
Interpretação:
A probabilidade de a carta ser uma dama, dado que é vermelha, é 1/13, ou aproximadamente 7,7%.
Exemplo 4: Lançamento de Dois Dados
Situação:
Considere dois dados lançados simultaneamente.
- Espaço amostral: S={(1,1),(1,2),…,(6,6)}, |S| = 36
- Evento A: A soma dos números é 10. A={(4,6),(5,5),(6,4)}, |A| = 3
- Evento B: O primeiro dado mostra 5. B={(5,1),(5,2),…,(5,6)}, |B| = 6
Cálculo de PP(A|B):
O espaço amostral é reduzido ao conjunto B. No novo espaço:
- A∩B= {(5,5)}, ∣A∩B∣ = 1
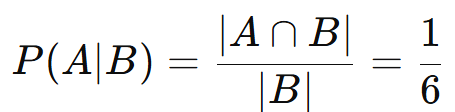
Interpretação:
A probabilidade de a soma ser 10, dado que o primeiro dado mostra 5, é 1/6, ou aproximadamente 16,7%.
Resumo e Fórmula da Probabilidade Condicional
A probabilidade condicional pode ser calculada de duas formas:
- Reduzindo o espaço amostral ao evento B:
Contar os resultados favoráveis a A no conjunto B. - Usando a fórmula geral:
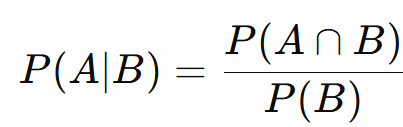
com P(B)>0
Conclusão
A probabilidade condicional é uma ferramenta essencial para analisar eventos interdependentes. Com ela, podemos ajustar cálculos probabilísticos para levar em conta informações adicionais. Os exemplos apresentados mostram como aplicar esse conceito em situações práticas, desde experimentos com dados até pesquisas e sorteios.













