Progressão Geométrica (PG)

Introdução

A Progressão Geométrica (PG) é uma sequência numérica onde cada termo, a partir do segundo, é obtido pela multiplicação do termo anterior por uma constante chamada razão. A PG é amplamente utilizada em diversas áreas do conhecimento, como finanças, biologia e física, especialmente em situações que envolvem crescimento ou decrescimento exponencial. Por exemplo, a taxa de crescimento populacional ou a depreciação de um bem podem ser modeladas por uma progressão geométrica.

Termo Geral

O termo geral de uma Progressão Geométrica é uma expressão que permite calcular qualquer termo da sequência a partir de sua posição ( n ). Dado o primeiro termo ( a₁ ) e a razão ( q ), o termo geral ( a_n ) pode ser expresso pela fórmula:

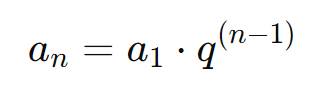
Onde:

• ( a_n ) é o n-ésimo termo da PG,
• ( a₁ ) é o primeiro termo da PG,
• ( q ) é a razão da PG,
• ( n ) é a posição do termo na sequência.

Essa fórmula é crucial para determinar qualquer termo de uma PG sem a necessidade de calcular os termos anteriores, facilitando o trabalho com grandes sequências.

Exemplo: Considere a PG onde a₁ = 3 e q = 2. Para encontrar o 5º termo a₅:

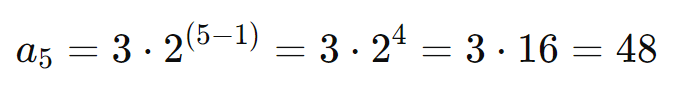
Razão

A razão ( q ) é a constante multiplicativa que gera o próximo termo da PG a partir do termo anterior. A razão pode ser positiva, negativa, maior que 1, entre 0 e 1, ou até mesmo zero. O valor da razão determina o comportamento da PG:

• ( q > 1 ): A sequência é crescente.
• ( 0 < q < 1 ): A sequência é decrescente.
• ( q < 0 ): A sequência é alternada, com sinais opostos.
• ( q = 1 ): A sequência é constante, ou seja, todos os termos são iguais.

A razão pode ser calculada pela divisão de qualquer termo pelo termo anterior:

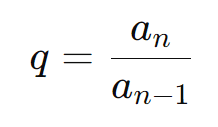
Exemplo: Seja uma PG com a₁ = 4 e a₂ = 12 . A razão q é:

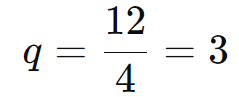
Termo Médio

Em uma Progressão Geométrica, o termo médio entre dois termos ( a_i ) e ( a_j ) é a raiz quadrada do produto desses termos. Se ( a_k ) é o termo médio entre ( a_i ) e ( a_j ), então:

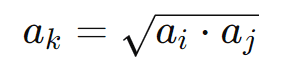
Essa propriedade é útil para determinar se uma sequência é uma PG e para encontrar um termo intermediário.

Exemplo: Considere a PG ( 3, 6, 12, 24, 48 ). O termo médio entre a₁ = 3 e a₃ = 12 é:

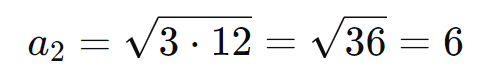
Soma dos Termos

A soma dos n primeiros termos de uma Progressão Geométrica finita depende do valor da razão ( q ):

• Quando ( q ≠ 1 ):

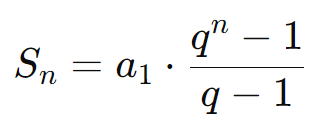
• Quando ( q = 1 ):

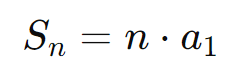
Onde:

• ( S_n ) é a soma dos n primeiros termos,
• ( n ) é o número de termos,
• ( a₁ ) é o primeiro termo,
• ( q ) é a razão.

Essa fórmula permite calcular rapidamente a soma de uma grande quantidade de termos sem somar cada um individualmente.

Exemplo:
Calcule a soma dos 5 primeiros termos da PG onde ( a₁ = 2 ) e ( q = 3 ):

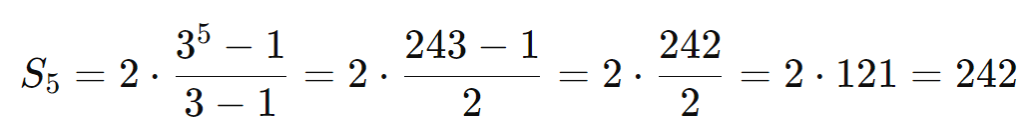
Soma no Infinito

A soma de uma Progressão Geométrica infinita ocorre quando o número de termos tende ao infinito. Essa soma existe apenas quando ( |q| < 1 ), ou seja, a razão está entre -1 e 1. A fórmula para a soma no infinito é:

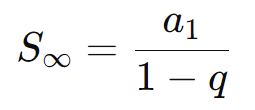
Onde:

• ( S_∞ ) é a soma infinita,
• ( a₁ ) é o primeiro termo,
• ( q ) é a razão com ( |q| < 1 ).

Essa fórmula é especialmente útil em aplicações práticas, como o cálculo de juros compostos e em séries geométricas.

Exemplo:
Considere a PG infinita onde a₁ = 10 e q = 0,5. A soma no infinito é:

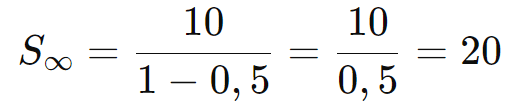
Conclusão

A Progressão Geométrica é uma sequência fundamental na matemática, com aplicações em diversas áreas do conhecimento. Compreender seu termo geral, razão, termo médio, soma e soma no infinito permite resolver uma ampla gama de problemas, especialmente aqueles relacionados ao crescimento exponencial e séries infinitas. A PG oferece uma ferramenta poderosa para modelar e analisar fenômenos que seguem padrões geométricos.

Leia também

Progressão Aritmética (PA)

Questões de Progressão Geométrica

1. Dada a PG: 2, 6, 18, 54, … Qual é o 6º termo dessa sequência?
   a) 324
   b) 486
   c) 729
   d) 972
2. Se o primeiro termo de uma PG é 3 e a razão é 5, qual é o valor do 4º termo?
   a) 75
   b) 90
   c) 105
   d) 125
3. Em uma PG, o 2º termo é 8 e o 5º termo é 64. Qual é a razão dessa progressão?
   a) 2
   b) 3
   c) 4
   d) 8
4. Determine a soma dos 4 primeiros termos de uma PG onde a1=5 e q=2.
   a) 15
   b) 30
   c) 45
   d) 75
5. Em uma PG, o 3º termo é 12 e o 6º termo é 96. Qual é o 8º termo?
   a) 192
   b) 288
   c) 384
   d) 768
6. Dada a PG: 7, 21, 63, 189, … qual é o 7º termo?
   a) 567
   b) 1701
   c) 5103
   d) 15309
7. Se o 2º termo de uma PG é 9 e o 4º termo é 81, qual é o 6º termo?
   a) 243
   b) 324
   c) 729
   d) 972
8. Calcule a soma dos 5 primeiros termos de uma PG onde a1=4 e q=3.
   a) 80
   b) 120
   c) 242
   d) 364
9. Em uma PG, o 1º termo é 1 e o 4º termo é 27. Qual é o valor do 6º termo?
   a) 81
   b) 108
   c) 162
   d) 243
10. Se o 3º termo de uma PG é 16 e o 7º termo é 256, qual é a soma dos 8 primeiros termos?
    a) 510
    b) 765
    c) 1020
    d) 1275

Gabarito

1. b
2. d
3. c
4. b
5. d
6. b
7. c
8. c
9. d
10. c