Considere o triângulo ABC representado abaixo:

Vamos prolongar o lado BC do triângulo ABC na extremidade C e tomar um ponto X no prolongamento, de modo que a semirreta CX seja oposta à semirreta CB.
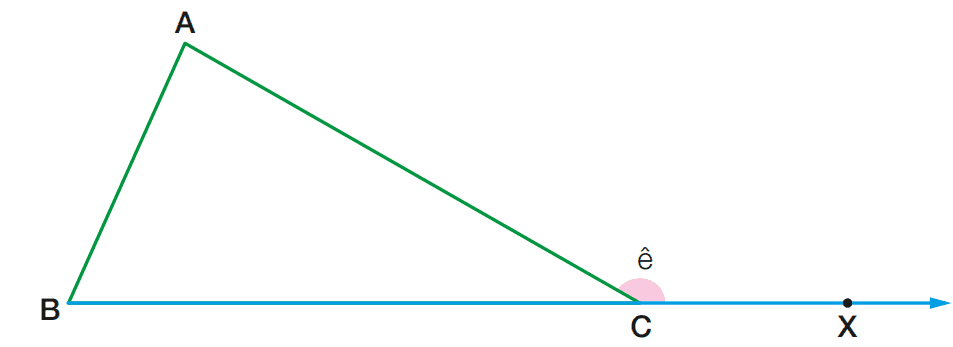
Dizemos que o ângulo ACˆX é um ângulo externo do triângulo ABC.
Observe que o ângulo externo ê = ACˆX é adjacente ao ângulo Cˆ do triângulo. Mas os ângulos Aˆ e Bˆ não são adjacentes ao ângulo externo ê
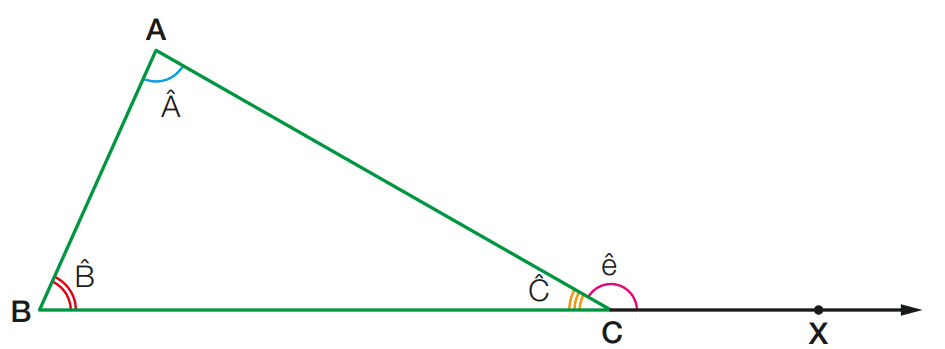
Observe, ainda, que:
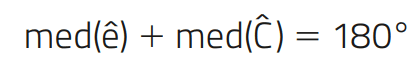
pois eˆ e Cˆ são adjacentes e suplementares
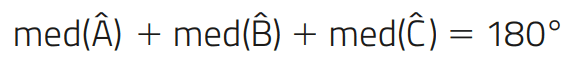
soma dos ângulos internos de um triângulo
Então, temos:
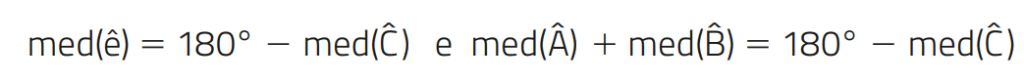
Logo,

Em todo triângulo, qualquer ângulo externo tem medida igual à soma das medidas dos dois ângulos internos não adjacentes a ele.
A geometria é uma área fundamental da matemática, dedicada ao estudo das formas, tamanhos e propriedades de figuras no plano e no espaço.
Leia também…