Os quadriláteros são figuras geométricas de quatro lados, presentes em diversas formas no nosso cotidiano, como na arquitetura, na arte e na natureza. Quatro dos quadriláteros mais comuns são o quadrado, o retângulo, o paralelogramo e o losango. Neste artigo, discutiremos as propriedades de cada um desses quadriláteros, focando na área, perímetro e diagonal.
A geometria é uma área fundamental da matemática, dedicada ao estudo das formas, tamanhos e propriedades de figuras no plano e no espaço.
1. Quadrado
Definição:
O quadrado é um quadrilátero regular, ou seja, todos os seus lados são iguais e todos os ângulos internos medem 90 graus.

Área:
A área de um quadrado é dada pelo produto do comprimento de dois de seus lados:
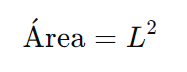
onde L é o comprimento de um dos lados.
Perímetro:
O perímetro de um quadrado é a soma de todos os seus lados:
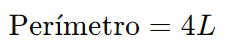
onde L é o comprimento de um dos lados.
Diagonal:
A diagonal de um quadrado pode ser calculada usando o Teorema de Pitágoras, já que a diagonal divide o quadrado em dois triângulos retângulos:
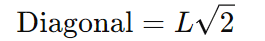
onde L é o comprimento de um dos lados.
2. Retângulo
Definição:
O retângulo é um quadrilátero onde os lados opostos são paralelos e iguais, e todos os ângulos internos são de 90 graus. Ele é um tipo de paralelogramo.

Área:
A área de um retângulo é dada pelo produto da sua base pela sua altura:
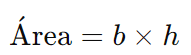
onde b é a base e h é a altura.
Perímetro:
O perímetro de um retângulo é a soma de todos os seus lados:
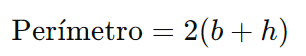
onde b é a base e h é a altura.
Diagonal:
A diagonal de um retângulo também pode ser calculada usando o Teorema de Pitágoras:
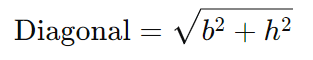
onde b é a base e h é a altura.
3. Paralelogramo
Definição:
Um paralelogramo é um quadrilátero onde os lados opostos são paralelos e iguais. Seus ângulos opostos também são iguais, mas não precisam ser ângulos retos.

Área:
A área de um paralelogramo é dada pelo produto da base pela altura:
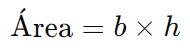
onde b é a base e h é a altura (a altura é a distância perpendicular entre as bases).
Perímetro:
O perímetro de um paralelogramo é a soma de todos os seus lados:
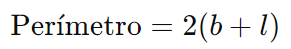
onde b é a base e l é o comprimento do lado lateral.
Diagonais:
As diagonais de um paralelogramo não são necessariamente iguais. Elas podem ser calculadas pela fórmula:
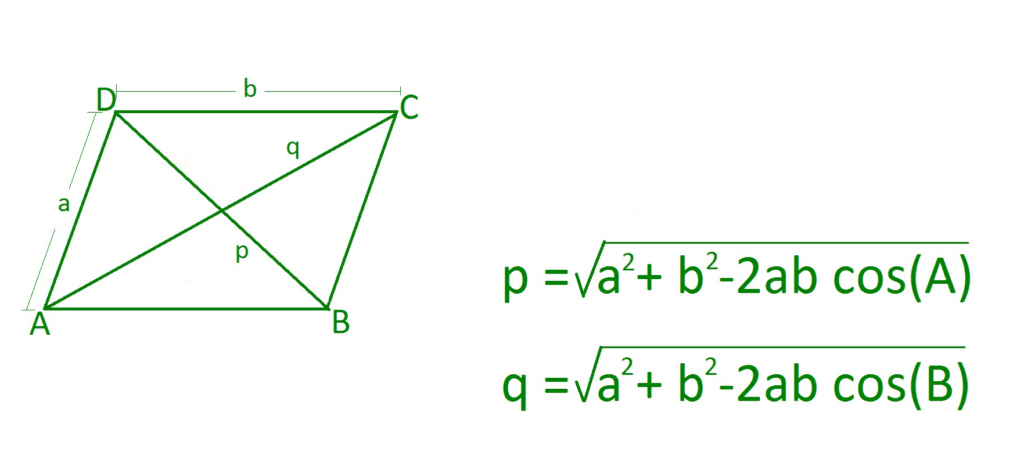
onde p e q são as diagonais, a e b são os comprimentos dos lados, e θ é o ângulo entre os lados.
4. Losango
Definição:
O losango é um quadrilátero onde todos os lados são iguais e os ângulos opostos são iguais. É um caso especial de paralelogramo.

Área:
A área de um losango pode ser calculada usando o produto das diagonais:
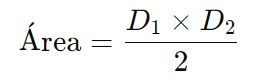
onde D1 e D2 são as diagonais do losango.
Perímetro:
O perímetro de um losango é a soma de todos os seus lados:
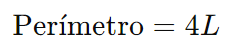
onde L é o comprimento de um dos lados.
Diagonais:
As diagonais de um losango se cruzam em ângulos retos e dividem-se ao meio. Se LLL for o lado do losango, as diagonais podem ser encontradas usando a relação:
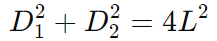
Conclusão
Os quadriláteros, especialmente o quadrado, retângulo, paralelogramo e losango, são fundamentais na geometria e possuem propriedades distintas que os tornam únicos. Entender as fórmulas para área, perímetro e diagonais é essencial para resolver problemas práticos envolvendo essas figuras. Esses conceitos são amplamente aplicados em diversas áreas, desde o design de edifícios até a criação de padrões artísticos.
Leia também
Área de Triângulos: Conceitos e Cálculos
Área de Figuras Planas: Como Calcular, Exercícios Resolvidos
Área de Circunferências: Explorando Formas e Cálculos
Explorando Ângulos: Agudo, Obtuso, Reto e Raso
Retas Paralelas e Transversais
A Soma dos Ângulos em Polígonos: Internos e Externos
Tudo Sobre Triângulos: Classificação e Propriedades
Congruência de Triângulos: Casos e Propriedades
Teorema de Pitágoras: Conceito, Provas e Aplicações
Relações Métricas no Triângulo Retângulo: Conceitos e Fórmulas Essenciais
A Lei dos Senos e a Lei dos Cossenos: Ferramentas Essenciais na Trigonometria
Quadriláteros: Área, Perímetro e Diagonais
Tudo Sobre Circunferência: Conceitos Essenciais e Cálculos
Inscrição e Circunscrição de Triângulos, Quadrados e Hexágonos Regulares
Quadriláteros Circunscritos: Teorema de Pitot
Relação Entre Retas e Circunferências: Corda, Tangente e Encontro de Tangentes
Ângulos na Circunferência: Uma Exploração Completa













